В статье рассматриваются инновационные системы на микро-уровне, приводятся базовые положения концепции сбалансированного распределения инновационных ресурсов предприятия между объектами инноваций. Определен вероятностно-выборочный метод для математического моделирования неоднородных совокупностей объектов инноваций на основе анализа случайных выборок их элементов, характеризуемых информационными флуктуациями. Предложен ряд распределений для оценивания оптимальности распределения инновационных ресурсов на случайных выборках из неоднородных совокупностей объектов инноваций.
Ключевые слова: инновационная система предприятия; концепция сбалансированного распределения инновационных ресурсов между объектами инноваций; многомерное структурированное гипергеометрическое распределение; вероятностно-выборочный метод, информационные флуктуации.
В течение последних 20 лет в практике и в исследованиях инновационной активности промышленных предприятий основной упор делался на реализации ими инновационных проектов. [1] Автор считает, что в настоящее время необходим переход от проектного подхода в организации нововведений к регулярному менеджменту инновационной деятельности, преобразование ее в системную компоненту производственного процесса. [2]
А это, в свою очередь, формулирует следующую проблему: если системность инновационной компоненты операционной деятельности промышленного предприятия выражается в планировании его инновационного развития, понимаемого как перманентный процесс нововведений, то он должен быть основан на сбалансированном (оптимальном) распределении инновационных ресурсов между технологическими, маркетинговыми и организационными объектами инноваций. [3]
Ответ на вопрос о структурном балансе инноваций, их динамической взаимосвязи и последовательности, оформленный в алгоритмы и модели, представляется актуальным и востребованным научным знанием со стороны менеджмента инновационноактивных организаций. Решение данной задачи позволит сформировать предпосылки для системного, целенаправленного инновационного развития промышленных предприятий, повышения их конкурентноспособности в условиях санкционных ограничений экономической системы России со стороны стран ЕС и США. Однако решать проблему экономической диспаритетности между объектами инноваций весьма затруднительно из-за отсутствия системных принципов организации инновационного процесса на микро-уровне, что проявляется в следующем [4]:
- предприятия не имеют выраженной инновационной стратегии и политики нововведений, перспективных планов инновационного развития;
- новшества формируются случайным образом, зачастую ассоциируются только с новыми товарами — продуктовыми технологическим новшествами.
Современные научно-теоретические представления на микро-уровне не могут в полной мере ответить и на ряд ключевых вопросов, а именно [5]:
- какова вариативность параметров инновационного потенциала предприятия применительно к различным отраслям;
- каковы методы оценки перспективной структуры баланса инновационных ресурсов — количественные отношения между технологическими, маркетинговыми и организационными инновациями;
- каковы динамические отношения, последовательность реализации процессных и продуктовых инноваций в практике хозяйственной деятельности промышленных предприятий.
Экономика 20 века ознаменовалась появлением огромного количества логически законченных, имеющих свойство универсальной переносимости информационных технологий, математических моделей и алгоритмов, использование которых может приносить достаточно точно прогнозируемые результаты. Умение правильно их использовать, комбинировать и «строить» из этих составных частей более сложные «конструкции» является уже просто необходимым условием развития любой инновационной системы предприятия.
Информационные и когнитивные технологии, наряду с технологиями информационных и управляющих систем, входят в перечень критических технологий современной России, определенных в Указе Президента России № 899 от 7 июля 2011 года, а также являются приоритетными направлениями развития науки, технологий и техники согласно «Прогнозу научно-технологического развития Российской Федерации на период до 2030 года».
Поэтому для оптимизации распределения инновационных ресурсов дальневосточных промышленных предприятий между объектами инноваций более перспективным, на наш взгляд, является путь математически корректного учета различий между инновационными системами как многомерными структурами неоднородной совокупности объектов инноваций и случайной выборки их элементов, характеризуемых качественными и количественными признаками, на этапе компьютерных расчетов. Этот подход пока не нашел заметного развития в работах российских исследователей, хотя, требуя значительного объема компьютерных расчетов, и решает указанную задачу.
Анализ качественных признаков процесса сбалансированного распределения инновационных ресурсов между инновациями на промышленных предприятиях неразрывно связан с обработкой разнотипных переменных. Методы решения этой проблемы могут быть связаны прежде всего с процедурами «оцифровки» слабых переменных. Однако объективно усилить шкалу измерения трудно, а тип «оцифровки» существенно предопределяет итоговые результаты всего процесса сбалансированного распределения инновационных ресурсов. Второй подход, идея которого связана со свойствами статистик бинарного отношения на множествах, основан на ослаблении всех переменных до булевого уровня с соответствующим увеличением размерности пространства признаков. При этом мы исходим из того, что любое сложное свойство инновационной системы предприятия может быть представлено как суперпозиция его более простых свойств.
Таким образом, имеется возможность декомпозиции свойств инновационных систем до некоторого «элементарного» (с практической точки зрения) уровня. В итоге мы получаем набор дихотомических признаков, описывающих изучаемую проблемно-ориентированную систему управления инновационной системой не только со стороны сбалансированности распределения инновационных ресурсов промышленных предприятий между объектами инноваций, но и со стороны оптимизации всей инновационной деятельности данного предприятия. [6]
В простейшем случае исследования генеральная совокупность инновационной системы предприятия представляет собой реализуемые им инновации. Пусть на исследуемом предприятии реализуется N инноваций, среди которых M = νN (0 < ν < 1) инноваций обладают интересующим нас дихотомическим признаком. Производится случайная выборка инноваций объема n. Вероятность того, что в выборку попадут m инноваций, обладающих изучаемым булевым признаком, задается в виде:
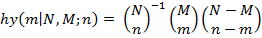(1)
Выражение (1) может быть представлено и в виде:
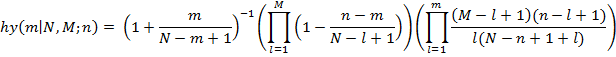
(2)
Выражение (2) «выгодно» отличается (в смысле его использования для машинных расчетов) от традиционных представлений, которые основаны на вычислениях (весьма медленно сходящихся) бесконечных сумм или произведений. Пусть случайным образом было исследовано n (n << N) объектов инноваций. В выборку объектов попало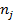 
инноваций,относящихся к j-й категории заданной классификации, среди которых «содержательным» признаком обладают 
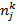инноваций. Их число в выборке, имеющих k-й изучаемый признак, равно
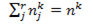(3)
Пусть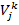 
— относительно частоты встречаемости k-го «содержательного» признака среди представителей J-й категории данной классификации:
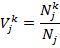(4)
Частота встречаемости k-го признака по объектам инноваций с помощью категорий априорных классификаций выражается в виде:
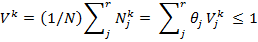(5)
Введем вектор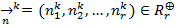 
. Вероятность 
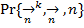того, что в случайной выборке объема инноваций n окажется по данной классификации структура 
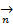и k-й признак будет зафиксирован в виде вектора 
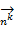, имеет вид:
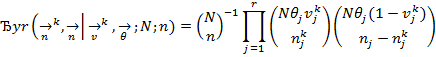(6)
Распределение вероятностей сбалансированности инновационных ресурсов промышленных предприятий между объектами инноваций (6) называется многомерным структурированным гипергеометрическим распределением (МСГГР).
Сегодня в работах российских ученых наблюдается тотальное использование квотных методик при исследовании проблемно-ориентированных систем управления и оптимизации инновационных ресурсов между объектами инноваций. Остановимся на вопросе стохастического обоснования их применения.
Прямые оценки частот встречаемости булевых признаков имеют вид:
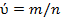(7)
При массовых исследованиях n << N, а гарантированные оценки погрешности частоты по правилу «трех сигм» оцениваются в виде:
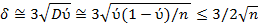(8)
Отсюда легко посчитать, что для выборочного портфеля порядка 1.5- 2.0 тыс. инноваций гарантированная погрешность частоты сбалансированности инновационных ресурсов между объектами инноваций равна примерно 3.5 %. Для точности оценок в 2 % нужно уже порядка 5.5 тыс. исследуемых объектов инноваций. А погрешности в 1 % требует исследования около 22.5 тыс. объектов инноваций. Рассмотрим суть метода квотного отбора объектов инноваций, между которыми инновационные ресурсы предприятия распределены сбалансированно.
Из выражения (8) также очевидно, что распределение квотного отбора объектов инноваций в силу произвольности значений vj невозможно привести к многомерному структурированному МСГГР, в вероятностном смысле строго описывающему случайный отбор. Однако, математическое ожидание суммы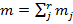 
объектов инноваций, обладающих изучаемым признаком, равно nν, где ν — истинная частота появления k-го признака среди всех элементов исследуемой совокупности инноваций и инновационных ресурсов, а ее дисперсия асимптотически стремится к нулю. Это значит, что квотная оценка частоты является несмещенной и состоятельной оценкой истинной частоты встречаемости изучаемого признака. Следовательно, использование квотных методик правомерно, но, как уже указывалось, сопряжено с невысокой точностью оценок, невозможностью оценить частоты встречаемости по категориям априорных классификаций, высокой стоимостью формирования выборки и низкой оперативностью получения данных.
При изучении большой генеральной совокупности объектов инноваций для анализа составляется схема из «содержательных объектов инноваций», между которыми инновационные ресурсы предприятия распределены сбалансированно, общее число вариантов выбора которых равно р. При выборе варианта используются априорные классификации по s номинальным шкалам, данные по которым есть на предприятии и в Росстате. Как и ранее, без потери в общности изложения, будем рассматривать только одну априорную классификацию, помня, что всего их s > 1. Пусть число категорий в данной классификации равно r.
Сохранив принятые выше обозначения, введем структурированное биномиальное распределение (СБР) вида:
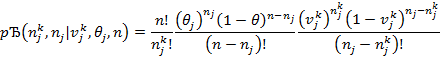(9)
СБР определяет вероятность того, что в выборке инновационных систем объема n обнаружено 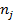объектов инноваций j-ой категории данной классификации, 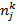из которых обладает k- м признаком.
Таким образом, если в серии с n выборов инновационных ресурсов предприятия с r «непрерывными» выборами между объектами инноваций рассматриваются абсолютные величины исходов, то мы имеем дело с выражением:
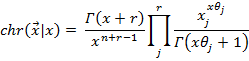(10)
Если же рассматриваются доли величин различных исходов, то его описывает распределение Дирихле:
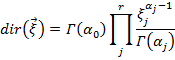(11)
Таким образом, предлагаемый нами подход позволяет:
во-первых, определить аналитический аппарат выборочного метода анализа инновационных систем промышленных предприятий как многомерных структур не только для случая неоднородной конечной совокупности объектов инноваций, но и для несчетных неоднородных множеств;
во-вторых, полученный нами ряд распределений вероятностей гипергеометрического и полиномиального вида позволяет построить процедуру оценивания оптимальности распределения инновационных ресурсов промышленных предприятий между объектами инноваций на случайных выборках из их неоднородных совокупностей, описываемых качественными и количественными признаками в рамках концепции их сбалансированного распределения для устранения диспаритетности.
Литература:
1. Лавриченко О. В. Декомпозиция задачи оптимизации сбалансированного распределения инновационных ресурсов промышленного предприятия между объектами инноваций // Молодой ученый.-2014.-№ 10(60).-С.164–168.
2. Лавриченко О. В. Инновационные бизнесобразующие технологии как эндогенная основа инновационной системы промышленного предприятия: монография.-М. Изд-во МосГУ.-136 с.
3. Лавриченко О. В. Интенциональность научной концепции сбалансированного распределения инновационных ресурсов промышленного предприятия между объектами инноваций // Молодой ученый.-2014.-№ 4(63).-С.565–570.
4. Лавриченко О. В. Математическое обеспечение системы сбалансированного распределения инновационных ресурсов промышленных предприятий между объектами инноваций // Журнал научных и прикладных исследований.-2014.-№ 5.-С.74–80.
5. Лавриченко О. В. Оптимизация инновационной системы предприятия в условиях сбалансированного распределения инновационных ресурсов между объектами инноваций // Научный обозреватель.-2014.-№ 7(43).-С.52–56.
6. Lavrichenko O. V. Intentionality of the theory of economics of active connect // Paradigmata poznani.-Prague.-2014.-№ 3.-p.22–28.
