В данной работе выведены формулы для объемов n-мерного симплекса и n-мерного параллелепипеда через коэффициенты уравнений их гиперграней. Полученные формулы могут быть использованы для решения различных задач, в частности при n=2 и n=3 в школьном курсе геометрии.
Для нахождения площади треугольника, стороны которого заданы уравнениями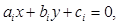 
где 
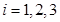известна формула
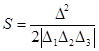, (1)
где 
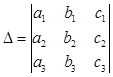, а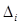 
- алгебраическое дополнение элемента 
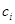. [1, c. 54]
Лемма. Для невырожденной квадратной матрицы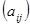 
порядка 
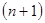выполняется следующее равенство
,
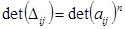где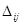 
- алгебраическое дополнение элемента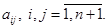
Доказательство. Используя невырожденность матрицы 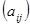, получим:
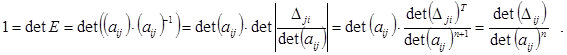
Откуда следует:
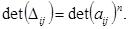
Теорема 1. Пусть гиперграни n-мерного симплекса заданы уравнениями
,
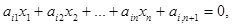
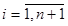тогда объем симплекса будет равен
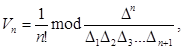(2)
где 
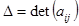и 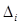- алгебраическое дополнение элемента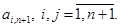
Доказательство. Пусть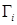 
– гипергрань симплекса в гиперплоскости, заданной уравнением 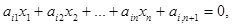где ,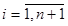 
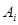– вершины симплекса, причем для 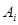выполняется условие
.
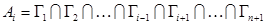В частности для вершины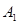 
получим:
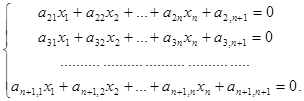
Решая систему по формулам Крамера, найдем координаты вершины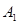 в виде:
.
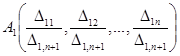Аналогично найдем координаты вершин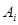, где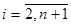 
:
.
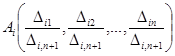Подставив координаты вершин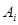, где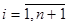 
, в известную формулу для объема n-мерного симплекса
,
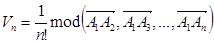получим:
.
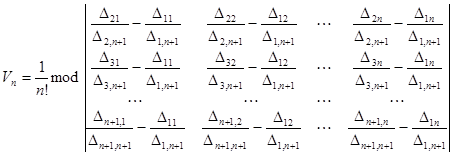Данное выражение преобразуем к более компактному виду:
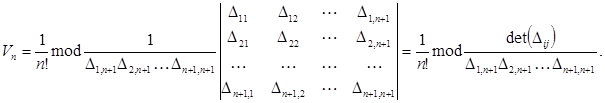
Откуда, используя лемму и обозначения данной теоремы, получим искомую формулу (2):
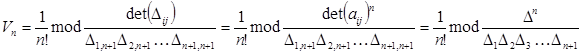
или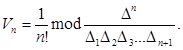 
Теорема 2. Пусть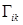 
-гиперграни n-мерного параллелепипеда заданы уравнениями
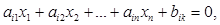
где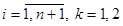 
, причем, 
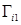и 
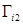параллельны между собой, тогда объем n-мерного параллелепипеда будет равен
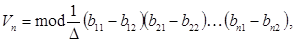(3)
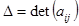где , где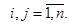
Доказательство. Перейдем от координат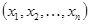 
к новым координатам 
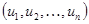по формуле:
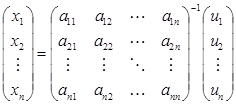. (4)
Якобиан преобразования (4) имеет вид:
.
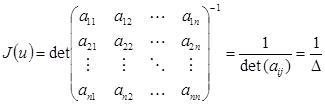После преобразования (4) получим прямоугольный n-мерный параллелепипед, уравнения гиперграней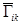 
которого, имеют вид:
.
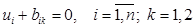Объем этого параллелепипеда равен:
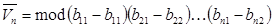. (5)
Искомый объем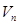 
и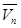 
связаны формулой:
.
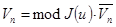Учитывая формулу (5), получим искомый объем 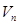n-мерного параллелепипеда:
.
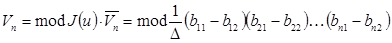Полученные формулы (2) и (3) применяются при решении различных задач. Заметим, что применение формул (2) и (3) является более рациональным и избавляет от трудоемких вычислений по сравнению со стандартными методами решений.
Задача 1. Докажите формулу
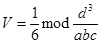
для вычисления объем пирамиды, ограниченной плоскостью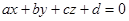 
и координатными плоскостями.
Задача 2. Докажите формулу
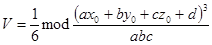
для вычисления объем пирамиды, ограниченной плоскостям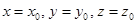и 
и .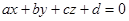
Решение. При n=3 вычислим определители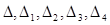 
:
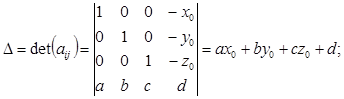
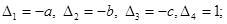
найдем объем данной пирамиды по формуле (2) при n=3:
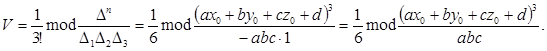
Задача 1 получается из задачи 2, при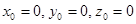 
.
Задача 3. Вычислить объем пирамиды, ограниченной плоскостям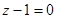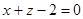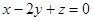и 
, 
, 
и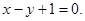 
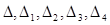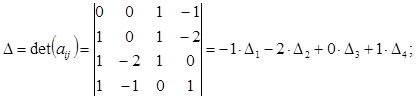
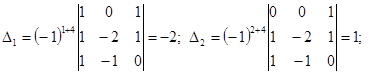
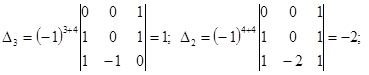
Решение. Вычислим определите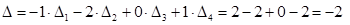ли :
или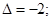 
Найдем объем пирамиды по формуле (3) при n=3:
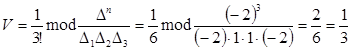или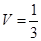 
.
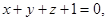
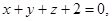
Задача 4. Вычислить объем параллелепипеда, ограниченного плоскостям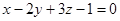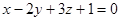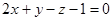и 
, 
, 
и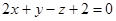 
.
Решение. Применим формулу (3) при n=3, получим:
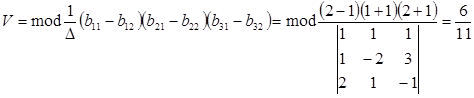или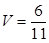 
.
Литература:
1. В. А. Садовничий, А. С. Подколзин. Задачи студенческих олимпиад по математике. М.: Наука, 1978.
2. http://ru.wikipedia.org/wiki/simplex
