Сызықта М нүктесін және ондағы жанаманы қарастырайық. Жақын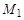 
нүктесіне көшкеннен жанама кейбір 
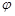бұрышына бұрылады. Осы 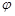бұрышының 
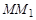доғасының 
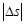ұзындығына 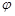/ 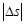қатынасы 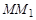доғасының орта қисықтығы делінеді. Ол ММ1 доғасының иілу дәрежесін орта есеппен сипаттайды. ММ1 доғасы өзінің түрлі нүктелерінде түрліше иілуі мүмкін. Алайда ММ1 доғасы неғұрлым кіші болған сайын, орта қисықтық осы доғаның әрбір нүктесіндегі иілу дәрежесін соғұрлым дәл анықтай түседі.
Анықтама. Сызықтың берілген М нүктесіндегі k қисықтығы деп сызықтың сол М және оған жақын М1 нүктелеріндегі жанамалары арасындағы 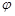бұрышының шексіз кіші ММ1 доғасының 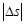ұзындығына қатынасының 
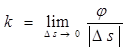шегін айтады.
Мысал ретінде R радиусты шеңбер қисықтығын анықтайық. Ол үшін оның бойында М және М1 нүктелерін алайық. Шеңбер жанамалары арасындағы бұрыш жанасу нүктелеріне жүргізілген ОМ және ОM1 радиустары арасындағы 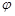бұрышына тең. Бір жағынан шеңбер доғасының 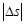ұзындығы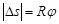 
көбейтіндісіне тең, мұнда 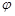- доғаны керетін централ бұрыш.
Сондықтан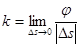 
=
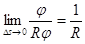
Демек, шеңбердің кез келген нүктесіндегі қисықтығы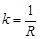 
атап айтқанда оның радиусына кері шама болып келеді.
Сызықтың М нүктесін және ондағы жанасушы жазықтығын қарастырайық. Сызық бойымен көрші М1 нүктесіне көшкенде жанасушы жазықтық қандайда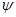 
бұрышына бұрылады осы 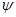бұрышының ММ1 доғасы 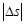ұзындығына қатынасын ММ1 доғасының орта бұралымы дейді. Ол кеңістік сызығының жазықтықтан ауытқуын орта есеппен сипаттайды. ММ1 доғасын кішірейте отыра, біз қисықтың берілген нүктесіндегі бұралым ұғымына келеміз.
Сызықтық берілген М нүктесіндегі æ бұралымы деп сол М және оған жақын орналасқан М1 сызық нүктесіндегі жанасушы жазықтықтары арасындағы 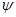бұрышының кіші ММ1 доғасының 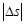ұзындығына қатынасының 
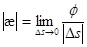шегін айтады.
Мұның өзінде сызық бойымен сырғытып жанасушы жазықтық оң бүрандалы қозғалыс жасайтын болса, бұралымы оң деп есептейміз, кері жағдайда - теріс болып саналады. Жанасушы жазықтықтың 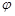айналу бұрышының орнына оған тең бинормальдың айналу бұрышын алуға болатынын атап кеткен орынды.
Қисықтық пен бұралымды анықтағанның өзінде-ақ қисықтың доға ұзындығы ұғымын пайдаланамыз. Енді бұл ұғымды қатаң анықтап, интеграл арқылы доға ұзындығын есептеуге арналған формуланы шығарып аламыз.
Сызық доғасының L ұзындығы деп оған іштей сызылған сызық ұзындығының, сызықтағы кесінділер санының шектеусіз өсіп, ең ұзын кесінді ұзындығы 0-ге ұмтылғандағы шегін айтамыз.
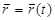сызығы АВ доғасы нүктелері және сәйкес 
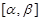кесіндіснен алынған t параметірлер арасындағы сәйкестік өзара бірмәнді болсын. Оның үстіне әдеттегідей 
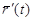туындысы бар болып ол үзіліссіз деп ұйғарамыз. Сызықың АВ доғасы ұзындығы
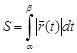
немесе
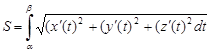
формуласы бойынша есептеледі.
Сызықтың tпараметірін S параметірімен алмастырғаннан алынған
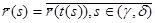
түріндегі L сызығының параметірленуін табиғи параметірлену деп, S параметірін табиғи (натурал) параметір дейміз.
Егер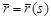 
L сызығының табиғи параметірленуі болса, 
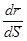векторы бірлік вектор, атап айтқанда 
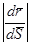=1 болады. Табиғи S параметірі сызықтың кейбір нүктесінен бастап саналатын доға ұзындығы болып табылады.
Егер барлық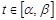 
нүктелері үшін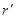 
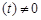болса, 
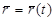сызығы регуляр, ал 
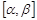кесіндісінің кезкелген ішкі нүктесі үшін 
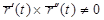болса, 
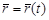сызығы бирегуляр делінеді.
Егер қисық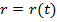 
теңдеуімен берілсе, онда қисықтық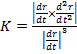 
ал бұралым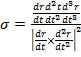 
алынған формулаларымен есептеледі.
Мысал. Қисықтың еркін нүктедегі қисықтығын есептеңіз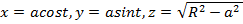 
t .
Шешімі: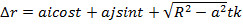 
, 
.
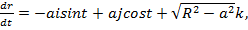
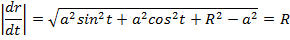
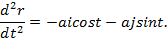
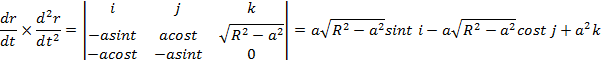
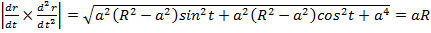Онда қисықтық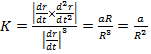 
. Бұралымды табу үшін 
.
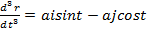Осы векторлардың аралас көбейтіндісін табамыз.
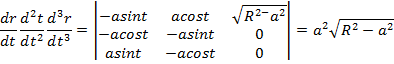
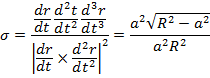
Материалды пысықтауға арналған тапсырмалар.
1. Қисықтың қисықтығын табыңыз: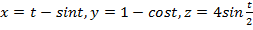 
(Жауабы: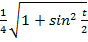
)
2. Қисықтың қисықтығын табыңыз: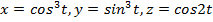 
(Жауабы: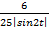 
)
3. Қисықтың қисықтығын және бұралымын есептеңіз: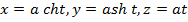 
(Жауабы: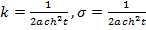 
).
Әдебиет:
1. Погорелов А.В. Геометрия. – Москва: Наука, 1984.
2. Мусин А.Т. Дифференциалдық геометрия және топология лементтері. - Алматы, 2014.
3. Александров А.Д., Нецветаев Н.Ю. Геометрия. – Москва: Наука, 1990.
4. Знаменская О.В., Кривоколеско В.П., Работин В.В. Дифференциальная геометрия и топология. - Красноярск, 2007.
