Рассматривается объект управления, описываемый уравнениями
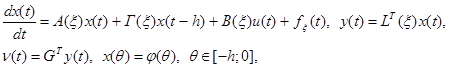
где 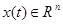 — вектор состояния;
— вектор состояния; 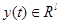 — вектор выхода;
— вектор выхода; 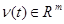 — обобщенный вектор выхода;
— обобщенный вектор выхода; 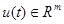 — вектор управления;
— вектор управления; 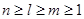 ;
; 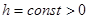 — величина запаздывания;
— величина запаздывания; 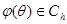 — начальная функция;
— начальная функция; 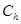 — пространство ограниченных непрерывных функций; A, Г, B, L — матрицы, числовые значения которых зависят от вектора неизвестных значений
— пространство ограниченных непрерывных функций; A, Г, B, L — матрицы, числовые значения которых зависят от вектора неизвестных значений 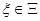 ;
; 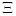 — известное множество;
— известное множество; 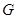 — постоянная матрица, элементы которой подлежат выбору;
— постоянная матрица, элементы которой подлежат выбору; 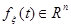 — вектор помех (возмущений), который может как удовлетворять неравенству
— вектор помех (возмущений), который может как удовлетворять неравенству
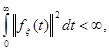 (1)
(1)
так и быть ограниченным по норме, но не затухающим во времени
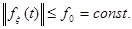 (2)
(2)
Структура адаптивного регулятора задана в виде 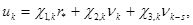
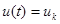 при
при 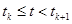 ,
,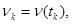
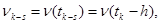 где
где 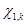 ,
, 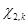 ,
, 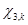 — матрицы настраиваемых коэффициентов регулятора;
— матрицы настраиваемых коэффициентов регулятора; 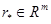 — постоянный вектор задающих воздействий;
— постоянный вектор задающих воздействий; 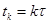 — дискретный аналог времени;
— дискретный аналог времени; 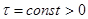 — шаг дискретизации;
— шаг дискретизации; 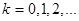 — номер шага; s — число тактов запаздывания, причем
— номер шага; s — число тактов запаздывания, причем 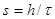 .
.
Задача 1. Если внешние помехи удовлетворяют соотношению (1), то при любых начальных условиях 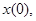
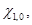
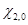 ,
, 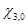 и
и 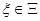 синтезировать систему адаптации, обладающую свойствами
синтезировать систему адаптации, обладающую свойствами
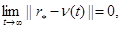
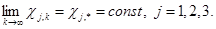 (3)
(3)
Задача 2. Если вектор возмущений 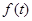 удовлетворяет ограничению (2), но противоречит условию (1), то при любых начальных условиях
удовлетворяет ограничению (2), но противоречит условию (1), то при любых начальных условиях 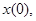
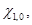
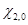 ,
, 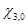 и
и 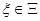 построить гибридную систему со свойствами
построить гибридную систему со свойствами
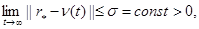
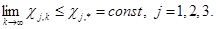
В рамках критерия гиперустойчивости можно показать, что достижение цели (3) возможно за счет следующих алгоритмов настройки регулятора:
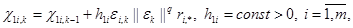
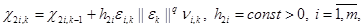 (4)
(4)
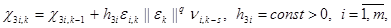
где 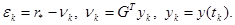
Для построения контура настройки, работоспособного в условиях постоянного действия внешних возмущений (2), проводят регуляризацию (огрубление) алгоритмов. Наиболее часто это достигается за счет введения в контур адаптации местных отрицательных обратных связей. Алгоритмы (4) в огрубленном виде могут быть представлены следующими робастными алгоритмами:
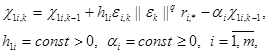
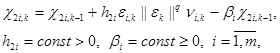 (5)
(5)
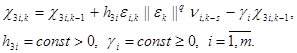
Литература:
1. Еремин Е. Л., Еремина В. В., Семичевская Н. П., Шевко Д. Г. Алгоритмы и S-модели гибридных систем адаптивного управления — Благовещенск, 2005. — 205 с.
2. Еремин Е. Л., Шевко Д. Г. Гибридная нелинейно преобразованная система прямого адаптивного управления // Радиоэлектроника, информатика, управление. — 2002. — № 2. — С. 142–147.
3. Еремин Е. Л., Шевко Д. Г. Имитационное моделирование технически эквивалентных гибридных систем управления // Информатика и системы управления. — 2001. — № 2. — С. 36–42.
4. Еремин Е. Л., Шевко Д. Г. Синтез и упрощение технической реализации гибридной нелинейно преобразованной системы прямого адаптивного управления // Вычислительные технологии. — 2003. — Т. 8, № 3. — С. 47–57.
5. Островерхий В. В., Шевко Д. Г. Задачи, решаемые автоматической системой управления шасси гусеничной машины // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. — 2011. — № 53. — С. 69–73.
6. Шевко Д. Г. Алгоритмы настройки для гибридной системы управления с запаздыванием // Молодой ученый. — 2014. — № 19. — С. 262–263.
7. Шевко Д. Г. Метод синтеза гибридных систем адаптации // Молодой ученый. — 2014. — № 21. — С. 251–253.
8. Шевко Д. Г. Гибридная система прямого адаптивного управления неминимально-фазовым объектом // Информатика и системы управления. — 2002. — № 1. — С. 112–120.
9. Шевко Д. Г. Критерий гиперустойчивости и синтез нелинейно-преобразованных гибридных систем прямого адаптивного управления // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. — 2012. — № 57. — С. 65–69.
10. Шевко Д. Г. Модели и алгоритмы нелинейно преобразованных гибридных систем прямого адаптивного управления: дис. … канд. техн. наук. — Благовещенск, 2003. — 149 с.
11. Шевко Д. Г. Модели и алгоритмы нелинейно преобразованных гибридных систем прямого адаптивного управления: автореф. дис. … канд. техн. наук. — Хабаровск, 2003. — 20 с.
12. Шевко Д. Г. Гибридная система прямого адаптивного управления неминимально-фазовым объектом // Информатика и системы управления. — 2002. — № 1(3). — С. 112–120.
13. Шевко Д. Г. Синтез алгоритмов самонастройки регулятора дискретной системы управления и сравнительный анализ качества процессов адаптации // Информатика и системы управления. — 2001. — № 1. — С. 97–105.
14. Шевко Д. Г. Синтез и нелинейные преобразования гибридных систем прямого адаптивного управления // Информатика и системы управления. — 2002. — № 2(4). — С. 133–144.

