1. Введение
В настоящее время одним из наиболее интересных направлений в робототехнике является разработка змееподобных роботов. Змееподобные роботы обладают рядом интересных возможностей, превосходящих способности традиционных роботов, использующих для передвижения колеса и конечности [1]. Основное из них — это исключительные способности передвижения по труднопроходимым территориям. Змееподобные роботы способны свободно перемещаться практически по любым видам поверхностей, а также в подвижных (сыпучих) и жидких средах. Кроме того, благодаря малому поперечному сечению подобные роботы способны передвигаться в ограниченных пространствах и узких местах, недоступных для традиционных роботов.
Другой отличительной особенностью змеевидных роботов является модульная структура и наличие большого количества степеней свободы (гиперизбыточность), что позволяет создавать отказоустойчивые модели. Поскольку любое движение подобных роботов основывается только на сгибании и разгибании сочленений, то выход из строя отдельных модулей не является критичным для работы всей системы и вызывает минимальное ухудшение рабочих характеристик. Кроме того, поскольку змееподобные роботы состоят из одинаковых элементов-модулей, то они проще и дешевле в изготовлении и ремонте.
Однако широкие возможности змееподобных роботов, связанные с гиперизбыточностью, имеют и обратную сторону — значительную сложность в управлении. В то время как для колесных и шагающих роботов традиционным подходом к созданию систем управления является ручное программирование человеком-разработчиком, для змеевидных роботов подобный подход оказывается малоэффективным. Из-за наличия большого количества степеней свободы разработчику крайне трудно заранее предусмотреть и запрограммировать все возможные формы передвижения и ситуации, когда их необходимо применять, и в особенности — учесть возможность адаптации в случае поломки отдельных модулей или неожиданного изменении окружающей среды. Поэтому становиться актуальным разработка способов автоматического порождения системы управления на основе различных моделей обучения [1,2].
В настоящее время для генерации систем управления гиперизбыточными роботами исследователи в основном отдают предпочтение эволюционным методам, в частности, генетическим алгоритмам и генетическому программированию [1,2]. Некоторые исследователи указывают на то, что таким образом удавалось находить решения, более эффективные, чем предлагались человеком-разработчиком [3]. Использование же других популярных методов, к примеру, обучение с подкреплением (Reinforcement Learning), оказывается затруднительным по причине наличия большего количества степеней свободы у подобных роботов.
Однако применение эволюционных методов также имеет существенные недостатки, основными из которых являются следующие. Во-первых, это существенное время, требуемое на проведение вычислений, поскольку на каждом эволюционном шаге каждое решение из популяции требует оценки эффективности способа перемещения. Во-вторых, это практическая невозможность применения данного метода для адаптации в условиях реальной работы, поскольку для работы метода необходимо наличие популяции роботов.
В предыдущих работах [4,5] нами была предложена модель нейронных контуров управления, состоящая их обучаемых логических нейронов, которая с успехом использовалась для обучения локомоции виртуальной модели нематоды C.Elegans. В данной работе мы попытаемся применить предложенную модель для обучения способам передвижения змееподобного робота, а также ответить на вопрос, возможно ли в принципе обучить искусственную систему управления сложным формам передвижения, демонстрируемым живыми существами, основываясь только на опыте взаимодействия системы с окружающей средой.
2. 3D симулятор змееподобного робота
Для проведения экспериментов с предложенной моделью управления был разработан интерактивный 3D-симулятор змеевидного робота с графическим интерфейсом. Основное назначение программы — проведение экспериментов по управлению роботами в среде, приближенной к реальному миру. Программа обладает возможностями визуализации виртуальной среды и записью экспериментов в видео-файл. В качестве физического движка в симуляторе используется библиотека Open Dynamic Library (ODE) [6], которая позволяет моделировать динамику твердых тел с различными видами сочленений. Преимуществом данной библиотеке является скорость, высокая стабильность интегрирования, а также встроенное обнаружение столкновений.
Модель змееподобного робота представлена в симуляторе в виде совокупности шести одинаковых прямоугольных блоков («позвонков»), соединенных вместе при помощи универсальных сочленений (рис. 1). Все сочленения идентичны и обладают двумя угловыми двигателями («мускулами»), обеспечивающими вращение суставов в вертикальной и горизонтальной плоскостях. Предложенная конструкция, несмотря на простоту, обеспечивает достаточную гибкость модели и позволяет принимать характерные для биологических змей положения тела.

Рис. 1. Модель змеевидного робота
3. Система управления локомоцией
В предыдущих работах [4,5] нами была предложена модель нейронного контура управления локомоцией нематоды C.Elegans, которая показала высокую эффективность в экспериментах по обучению волнообразному способу передвижения. Схема данного контура предполагала, что головная часть нематоды выступает в качестве источника колебаний, основываясь только на обратной связи от рецептора растяжения. Далее сигнал распространяется по телу нематоды с некоторой временной задержкой, обеспечивая тем самым характерное волнообразное движение. Поскольку конструкция змеевидного робота имеет много общих черт с моделью нематоды, то в данной работе мы решили использовать похожую схему нейронного контура для управления движением робота.
Мы выбрали нейронный контур, состоящий из 5 нейронов (рис. 2). Каждый нейрон 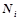 ,
, 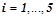 контролирует один сустав тела робота, подавая активирующие сигналы на угловые двигатели, расположенные в этом суставе. Головной нейрон
контролирует один сустав тела робота, подавая активирующие сигналы на угловые двигатели, расположенные в этом суставе. Головной нейрон 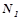 получает на вход информацию об углах сгиба между головным и последующим сегментом. Помимо этого на вход нейрона по обратным связям поступает сигнал от его собственного выхода с временной задержкой
получает на вход информацию об углах сгиба между головным и последующим сегментом. Помимо этого на вход нейрона по обратным связям поступает сигнал от его собственного выхода с временной задержкой 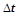 . Остальные нейроны
. Остальные нейроны 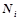 ,
, 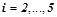 получают на свой вход только сигнал от выхода предыдущего нейрона
получают на свой вход только сигнал от выхода предыдущего нейрона 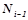 с временной задержкой
с временной задержкой 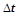 .
.
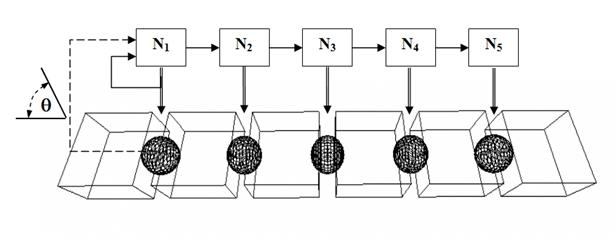
Рис. 2. Схема нейронного контура управления локомоцией
Работа нейронов определяется множеством логических закономерностей с оценками, имеющих следующий вид:
где 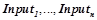 — множество предикатов, описывающих входящие сигналы нейрона,
— множество предикатов, описывающих входящие сигналы нейрона, 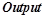 — предикат, описывающий выходящий сигнал нейрона,
— предикат, описывающий выходящий сигнал нейрона, 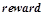 — награда, максимизация которой является постоянной задачей всего нейронного контура. Данные закономерности предсказывают, что если на вход нейрона будут поданы сигналы, описываемые предикатами
— награда, максимизация которой является постоянной задачей всего нейронного контура. Данные закономерности предсказывают, что если на вход нейрона будут поданы сигналы, описываемые предикатами 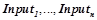 , и нейрон подаст на свой выход сигнал, описываемый предикатом
, и нейрон подаст на свой выход сигнал, описываемый предикатом 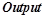 , то математическое ожидание награды будет равно некоторой величине
, то математическое ожидание награды будет равно некоторой величине 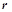 .
.
Множество входных и выходных предикатов для нейронов задается путем квантования диапазона возможных значений соответствующих входов и выходов нейрона. Награда для всего нейронного контура управления локомоцией определяется в зависимости от величины скорости, которую разовьет змеевидный робот на отрезке времени 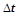 : чем выше скорость — тем больше награда.
: чем выше скорость — тем больше награда.
Функционирование нейрона происходит следующим образом. Предположим, что в некоторый момент времени на вход нейрона поступает набор входящих сигналов. В процессе принятия решения нейрон отбирает среди множества закономерностей, определяющих его работу, все такие закономерности, у которых предикаты 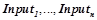 из условия правила выполняются на текущем наборе входящих сигналов. Затем среди всех отобранных закономерностей выбирается одна закономерность
из условия правила выполняются на текущем наборе входящих сигналов. Затем среди всех отобранных закономерностей выбирается одна закономерность 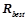 , имеющая максимальное значение математического ожидания награды
, имеющая максимальное значение математического ожидания награды 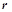 . После чего на выход нейрона подается выходной сигнал
. После чего на выход нейрона подается выходной сигнал 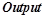 , указанный в условии закономерности
, указанный в условии закономерности 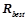 .
.
В начальной стадии функционирования нейрона, когда множество закономерностей, описывающих работу нейрона еще пусто, либо когда нет правил, применимых к текущему набору входящих сигналов, выход нейрона определяется случайным образом.
Обучение нейрона заключается в нахождении множества закономерностей вида , определяющих его работу. Для нахождения закономерностей используется алгоритм семантического вероятностного вывода, описанный в работах [7], при помощи которого анализируется множества данных, хранящих статистику работы нейрона (вход-выход нейрона и полученная награда) и извлекаются все статистически значимые закономерности вида .
Поскольку нейроны  имеют одинаковую структуру входных и выходных связей, то для увеличения скорости обучения этих нейронов мы решили объединить их опыт. Т. е. при обучении каждого конкретного нейрона из этой группы мы, помимо его собственной статистики, также использовали статистику работы всех остальных нейронов группы. Конечно, объединяя опыт данных нейронов, мы несколько ограничиваем возможные способы передвижения, которые могут быть обнаружены в ходе обучения, однако взамен мы получаем значительное увеличение скорости обучения.
имеют одинаковую структуру входных и выходных связей, то для увеличения скорости обучения этих нейронов мы решили объединить их опыт. Т. е. при обучении каждого конкретного нейрона из этой группы мы, помимо его собственной статистики, также использовали статистику работы всех остальных нейронов группы. Конечно, объединяя опыт данных нейронов, мы несколько ограничиваем возможные способы передвижения, которые могут быть обнаружены в ходе обучения, однако взамен мы получаем значительное увеличение скорости обучения.
4. Результаты
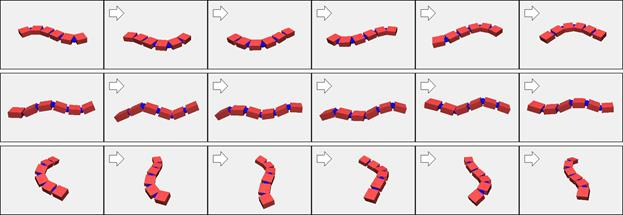
Рис. 3. Найденные системой способы передвижения
Используя симулятор змеевидного робота, был проведен ряд успешных экспериментов по обучению предложенной модели способам передвижения. В серии экспериментов системе управления удалось обнаружить три различных способа передвижения (рис. 3). Первый из найденных способов основан на волнообразном движении туловища в горизонтальной плоскости. Данный способ передвижения является самым распространенным среди биологических змей, а также характерен и для некоторых других животных, к примеру, нематод. Второй способ передвижения осуществляется за счет волнообразных движений в вертикальной плоскости и напоминает движение гусеницы. Последний способ движения основан на одновременном пропускании волны и в горизонтальной и в вертикальной плоскости. При этом тело робота как бы накручивается на невидимый цилиндр. Похожий способ перемещения использую некоторые виды змей, живущие в пустыне.
Таким образом, полученные результаты показывают, что предложенная модель системы управления способна обучиться сложным формам передвижения, основываясь только на опыте взаимодействия системы с окружающей средой. Примечательно, что найденные моделью способы движения встречаются в живой природе, в том числе среди змей. С практической точки зрения, результаты экспериментов показывают, что предложенная в данной работе модель системы управления является достаточно эффективной и может быть использована для управления сложными объектами, имеющими множество степеней свободы.
Литература:
1. Dowling K. Limbless locomotion: Learning to crawl with a snake robot. — Ph.D. dissertation, Robotics Inst., Carnegie Mellon Univ., Pittsburgh, PA, 1997.
2. Tanev I., Ray T., Buller A. Automated Evolutionary Design, Robustness and Adaptation of Sidewinding Locomotion of Simulated Snake-like Robot. — IEEE Transactions on Robotics. — V.21. — N. 4. — August 2005. — pp.632–645.
3. Koza J. R., Keane M. A., Yu J., Bennett F. H., Mydlowec W. Automatic creation of human-competitive programs and controllers by means of genetic programming // Genetic Program. Evolvable Mach. — 2000. — V. 1. — N. 1–2. — pp. 121–164.
4. Демин А. В. Обучающаяся модель управления хемотаксисом нематоды C.Elegans // Нейроинформатика. — 2013. — Т. 7. — № 1. — С. 29–41.
5. Demin A. V., Vityaev E. E. Learning in a virtual model of the C. elegans nematode for locomotion and chemotaxis // Biologically Inspired Cognitive Architectures (2014). — Elsevier, 2014. — V. 7. — pp. 9–14.
6. Smith R. Open Dynamics Engine. — URL: http://ode.org/.
7. Витяев Е. Е. Извлечение знаний из данных. Компьютерное познание. Модели когнитивных процессов. — Новосибирск: НГУ, 2006. — 293 с.
[1] Работа выполнена при финансовой поддержке интеграционного проекта РАН № 15/10 и гранта РФФИ № 14–07–00386.
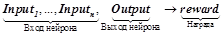 ,
, 
