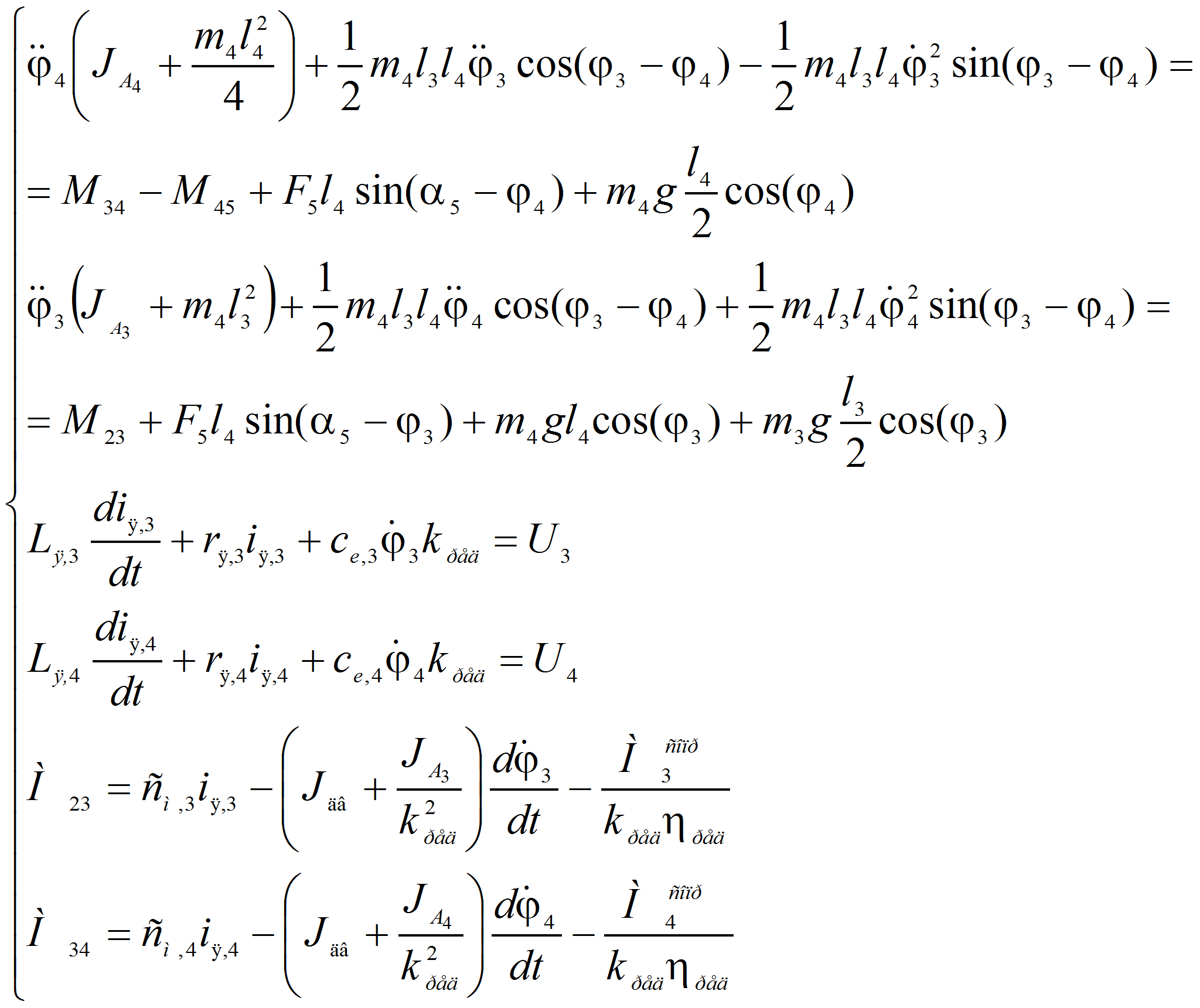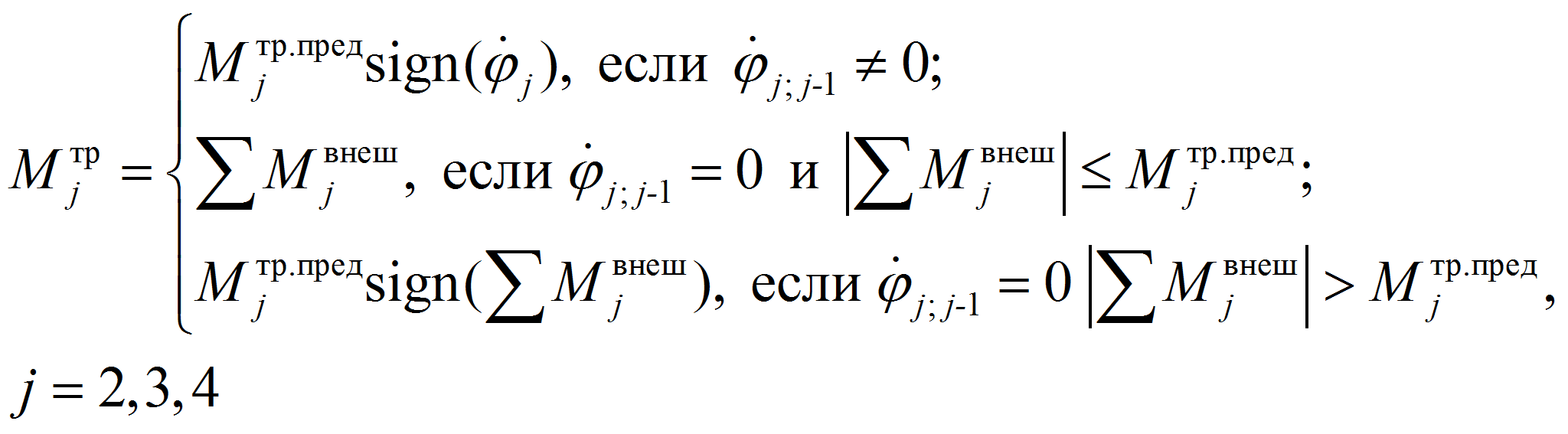- В данной работе рассмотрена математическая модель шестизвенного плоского мобильного робота для мониторинга трубопроводов переменного сечения. Предложен оригинальный алгоритм расчета и показаны результаты численного моделирования движения звеньев с учетом моментов сил трения в шарнирных соединениях робота.
-
- Введение. На сегодняшний день, изучению динамики многозвенных систем уделяется достаточно большое внимание [1–4]. В данной работе рассматривается математическая модель движения звеньев многозвенного мобильного робота, предназначенного для задач мониторинга внутренних поверхностей трубопроводов [5–6].
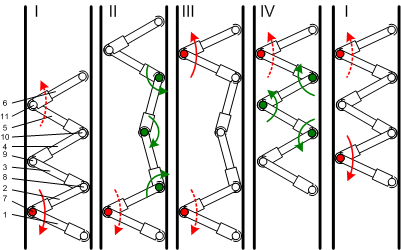
- Описание конструкции и принципа перемещения робота. Робот представляет собой шестизвенную конструкцию. Звенья 1–6 соединены между собой посредством мотор-редукторов вращательного движения 7–11 (рис. 1.). Рассмотрим алгоритм перемещения устройства по вертикальному прямолинейному отрезку трубопровода.
Рис. 1. Фазы движения внутритрубного робота
- Выделим 4 отдельные фазы движения робота: I фаза: режим силового удержания пары звеньев 5–6 и расклинивание пары звеньев 1–2 между стенок трубы; II фаза: режим силового удержания пары звеньев 1–2 и перемещение средней пары звеньев; III фаза: расклинивание пары звеньев 5–6 при силовом удержании пары звеньев 1–2; IV фаза: режим силового удержания пары звеньев 5–6 и перемещение средней пары звеньев.
- Математическое моделирование процесса удержания робота за счет сил трения под действием переменных внешних сил описано в работах [7–8]. Рассмотрим математическое моделирование движения средних звеньев при их перемещении согласно алгоритму, приведенному на рис. 1. Особенностью рассматриваемой модели является учет моментов сил трения, действующих в шарнирах и представленных в виде сложных зависимостей от скоростей относительного вращения звеньев.
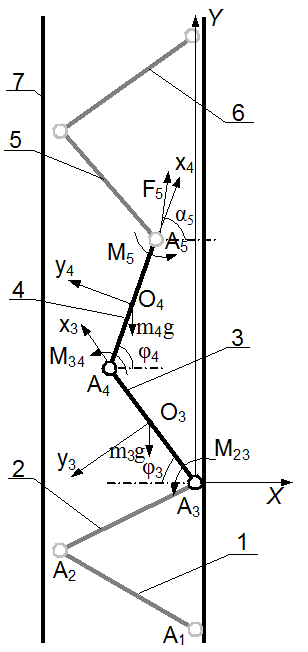
- Математическая модель движения средних звеньев внутритрубного робота. Расчетная схема устройства показана на рис. 2.
Рис. 2. Расчетная схема робота в режиме перемещения средних звеньев
- На данном
рисунке: звенья 1 и 2 осуществляют фиксацию робота внутри
трубопровода за счет сил трения. Точку А3
считаем неподвижной. Введем неподвижную систему координат с центром
в точке А3,
при этом ось А3Y
направлена по линии действия силы тяжести. Звенья 3 и 4 осуществляют
перемещение переднего фиксирующего модуля (звенья 5 и 6) под
действием крутящих моментов M23
и M34.
Со стороны верхнего ФМ на звенья действуют крутящий момент M45
и сосредоточенная
сила F5
приложенная под углом
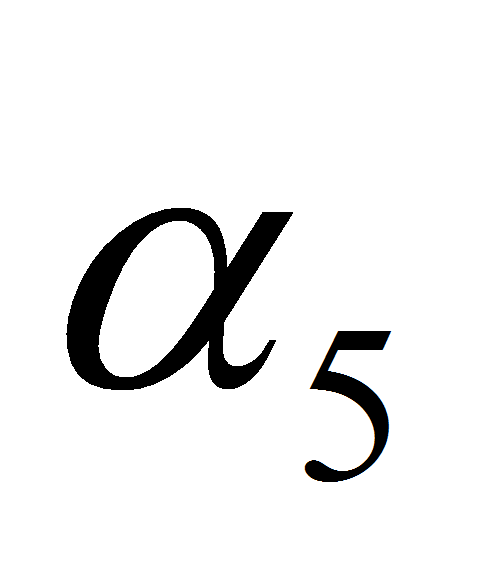 в точке А5.
Примем, что центры масс звеньев A3А4
и A4А5
расположены в их
геометрических центрах O3,
O4.
Системы координат X3Y3O3
и X4Y5O4
связаны с центрами масс звеньев.
в точке А5.
Примем, что центры масс звеньев A3А4
и A4А5
расположены в их
геометрических центрах O3,
O4.
Системы координат X3Y3O3
и X4Y5O4
связаны с центрами масс звеньев. -
В качестве обобщенных координат
примем углы поворота звеньев относительно их центров масс
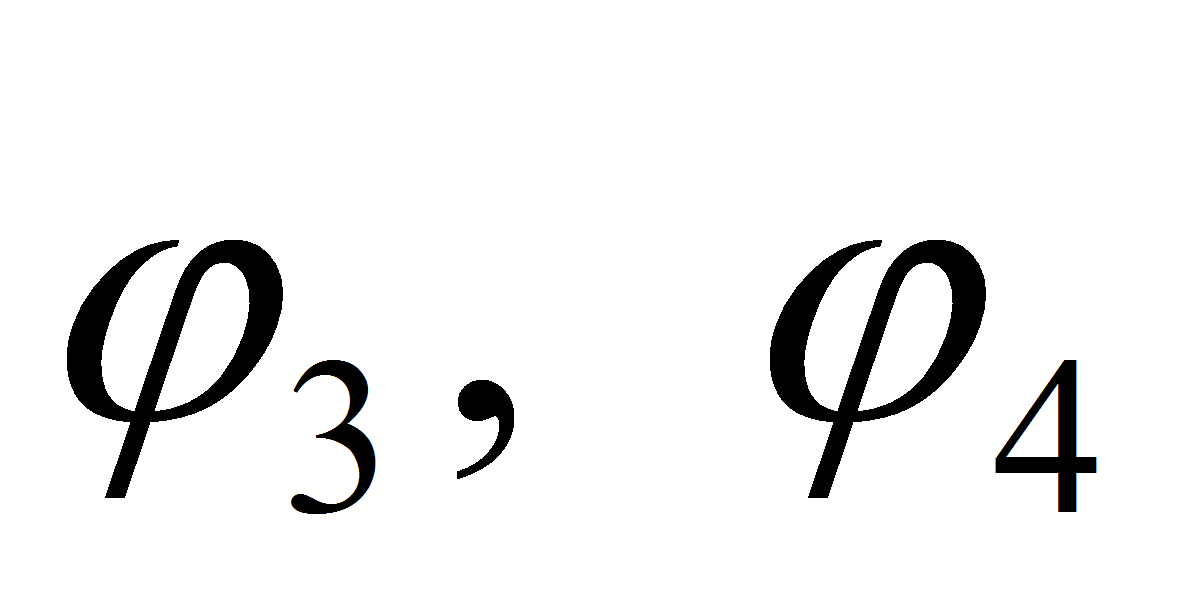 и
якорные токи
и
якорные токи
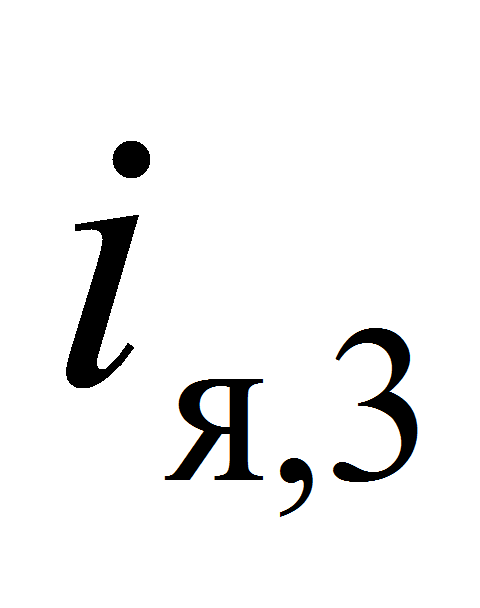
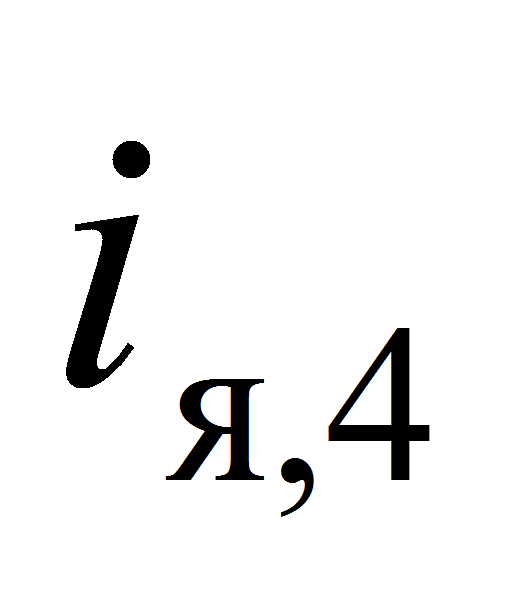 ,
электроприводов расположенных в местах соединений звеньев 2, 3
и 3, 4 соответственно. Для описания динамики движения звеньев
запишем дифференциальные уравнения, основываясь на уравнениях
Лагранжа 2-го рода. Для описания процессов происходящих
в электроприводах запишем второй закон Кирхгофа для цепи якоря,
а момент развиваемый приводом представим как произведение
моментного коэффициента двигателя
,
электроприводов расположенных в местах соединений звеньев 2, 3
и 3, 4 соответственно. Для описания динамики движения звеньев
запишем дифференциальные уравнения, основываясь на уравнениях
Лагранжа 2-го рода. Для описания процессов происходящих
в электроприводах запишем второй закон Кирхгофа для цепи якоря,
а момент развиваемый приводом представим как произведение
моментного коэффициента двигателя
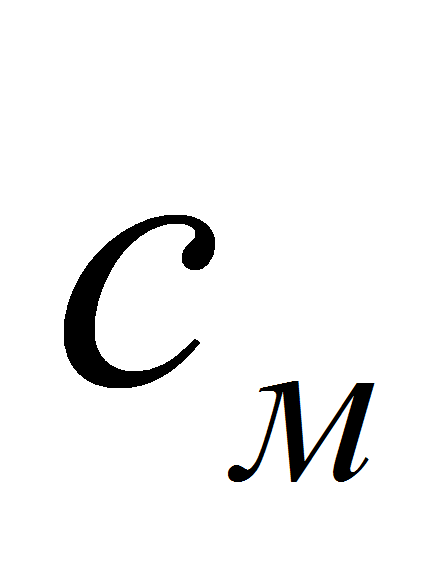 на ток якоря [7].
на ток якоря [7]. - Система дифференциальных уравнений, описывающая движения робота, будет иметь вид:
|
(1) |
- В этих
уравнениях:
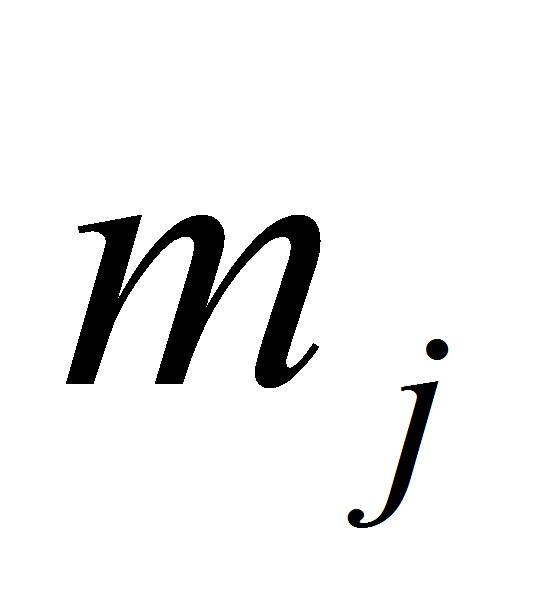 —
масса j-того
звена;
—
масса j-того
звена;
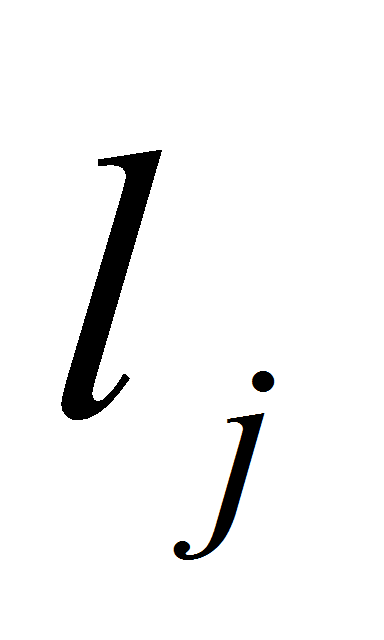 -
длина j-того
звена;
-
длина j-того
звена;
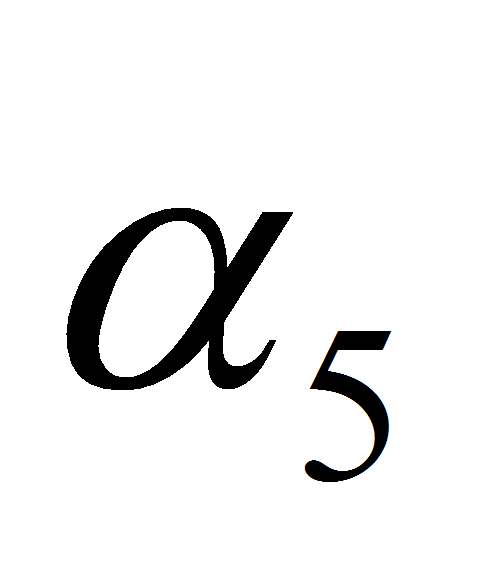 -
угол приложения внешней силы (равен 0 — сила приложена
вертикально вниз)
-
угол приложения внешней силы (равен 0 — сила приложена
вертикально вниз)
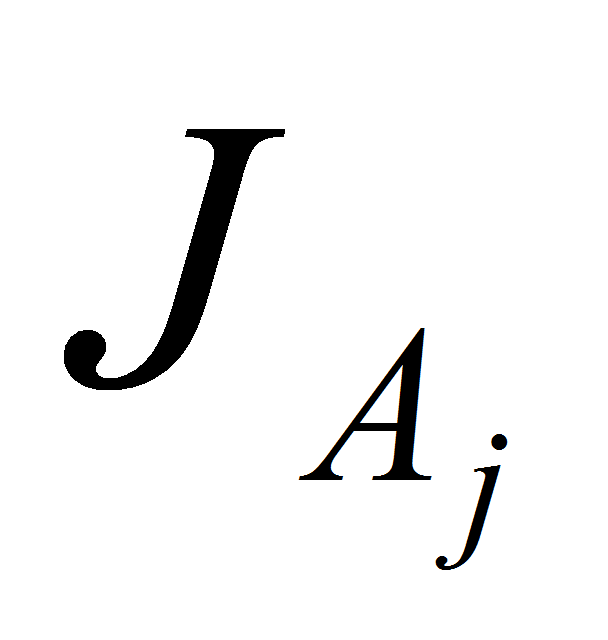 -момент
инерции j-тых
звеньев;
-момент
инерции j-тых
звеньев;
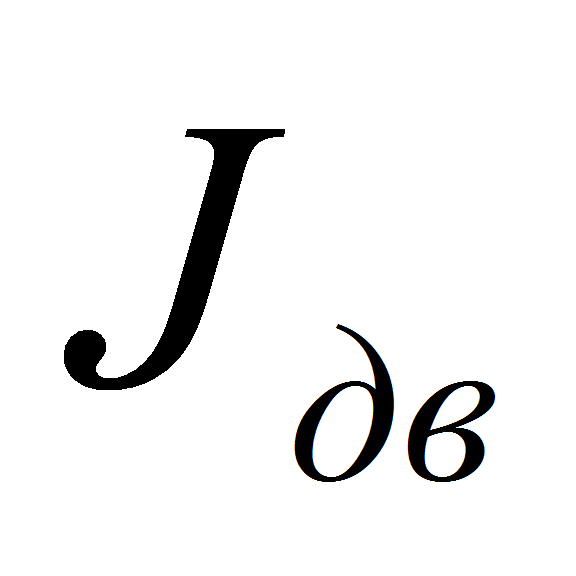 -
момент инерции электродвигателя; Lя,j
и rя,j —
индуктивность и сопротивление цепи якоря;
-
момент инерции электродвигателя; Lя,j
и rя,j —
индуктивность и сопротивление цепи якоря;
 и
и
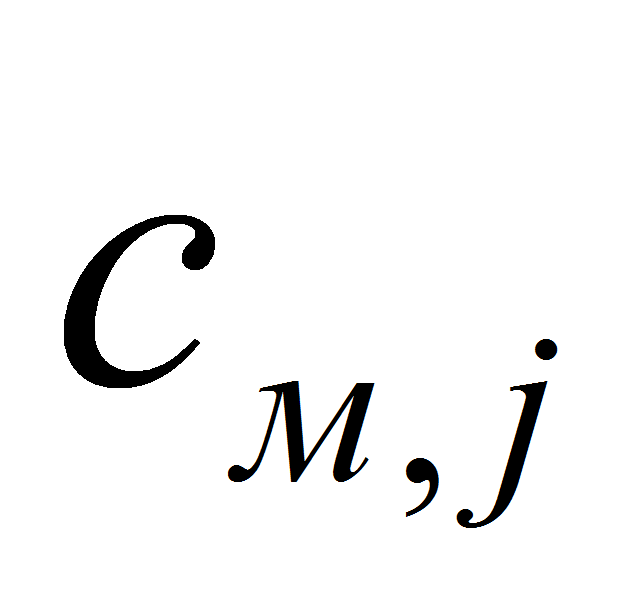 —
электрический и электромеханический коэффициенты
пропорциональности для j-того
двигателя; Uj —
управляющее напряжение на j-том
двигателе,
—
электрический и электромеханический коэффициенты
пропорциональности для j-того
двигателя; Uj —
управляющее напряжение на j-том
двигателе,
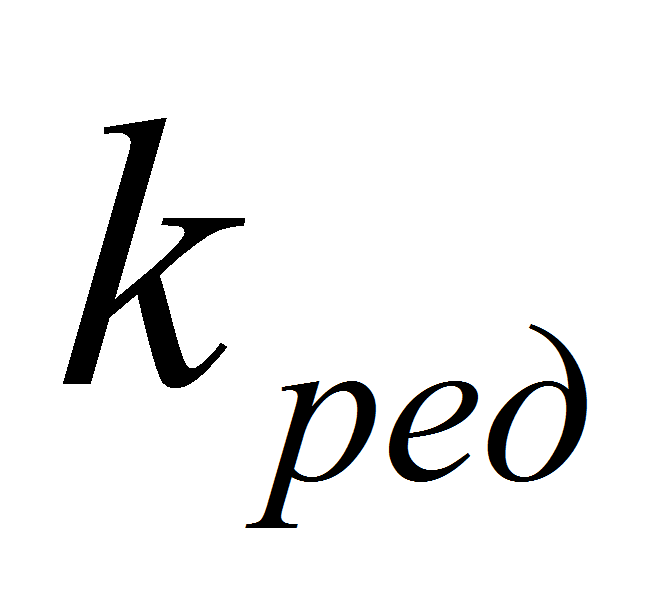 —
передаточное отношение редуктора
—
передаточное отношение редуктора
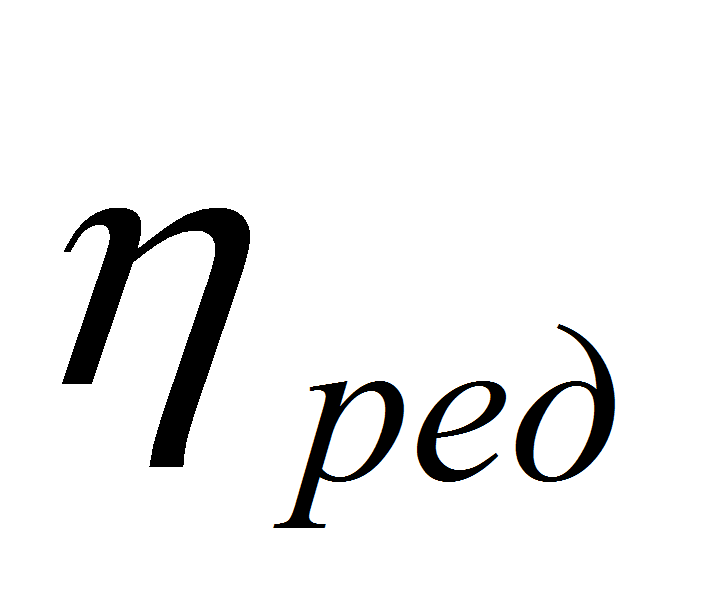 —
общий КПД электродвигателя.
—
общий КПД электродвигателя. -
Рассмотрим моменты
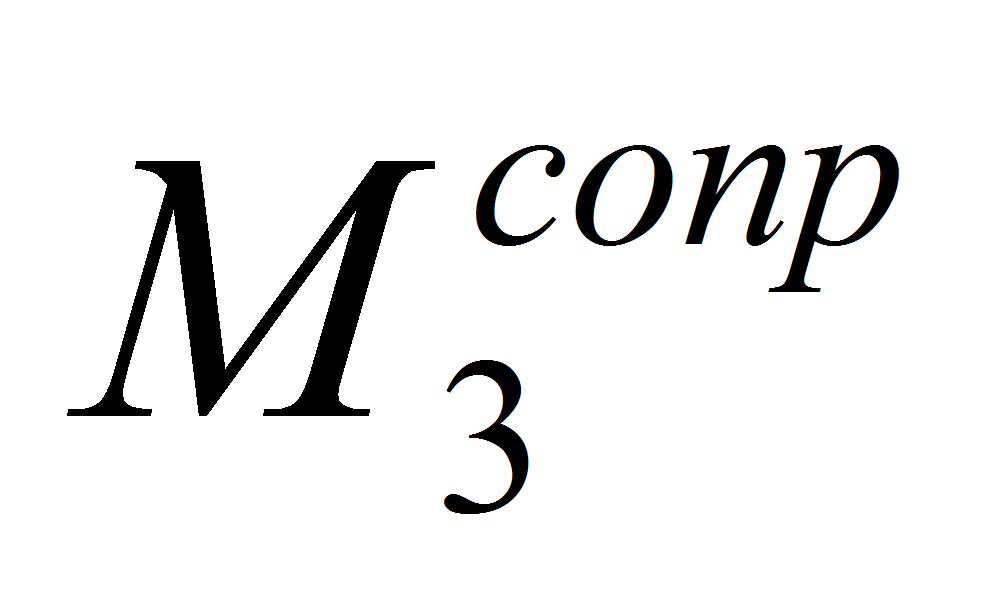 и
и
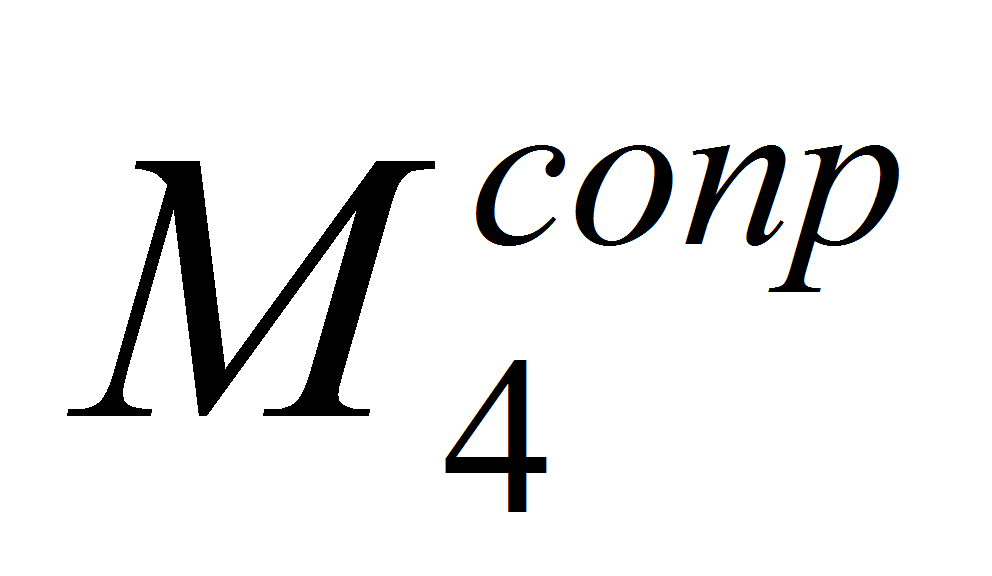 .
Представим момент сопротивления как:
.
Представим момент сопротивления как:
|
(2) |
где
![]() -
коэффициент вязкого сопротивления,
-
коэффициент вязкого сопротивления,
![]() —
суммарный момент сил трения в j-том
шарнире, определяемый следующим образом:
—
суммарный момент сил трения в j-том
шарнире, определяемый следующим образом:
|
(3) |
- где
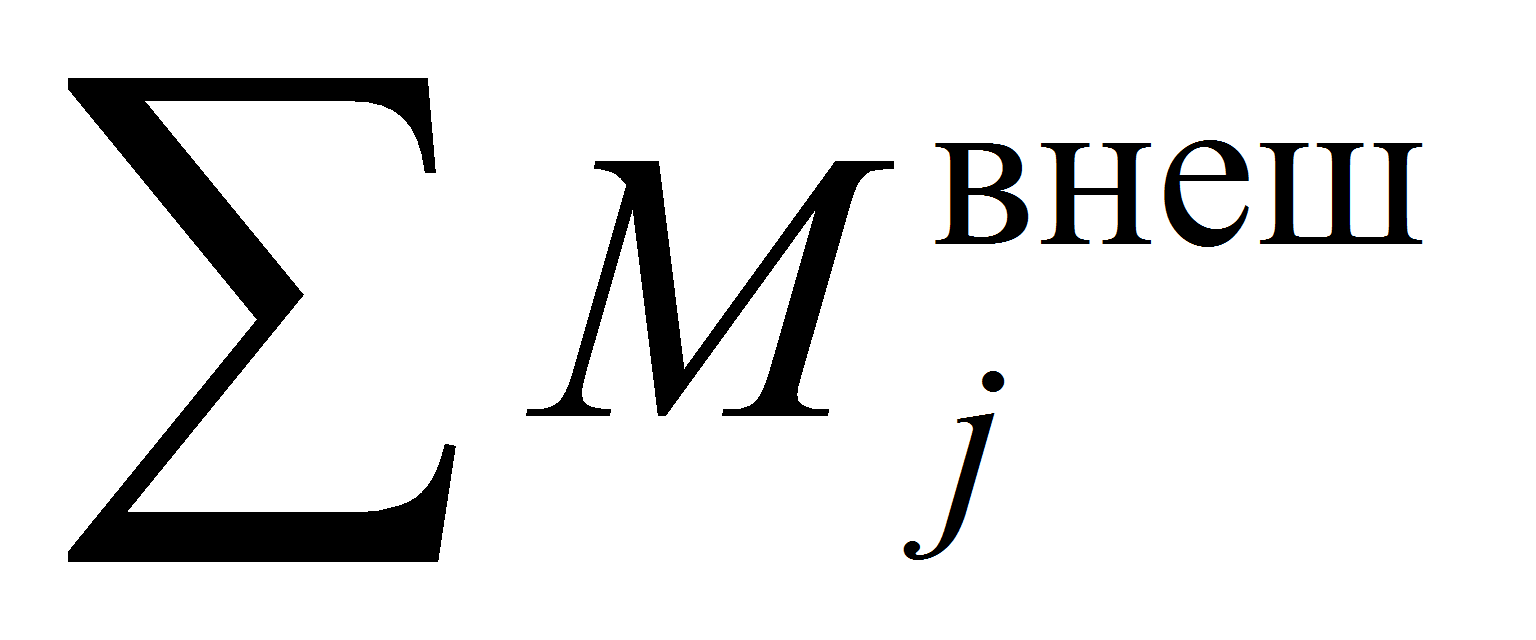 –
равнодействующая всех внешних моментов для j-того
шарнира, кроме моментов сил сухого трения;
–
равнодействующая всех внешних моментов для j-того
шарнира, кроме моментов сил сухого трения;
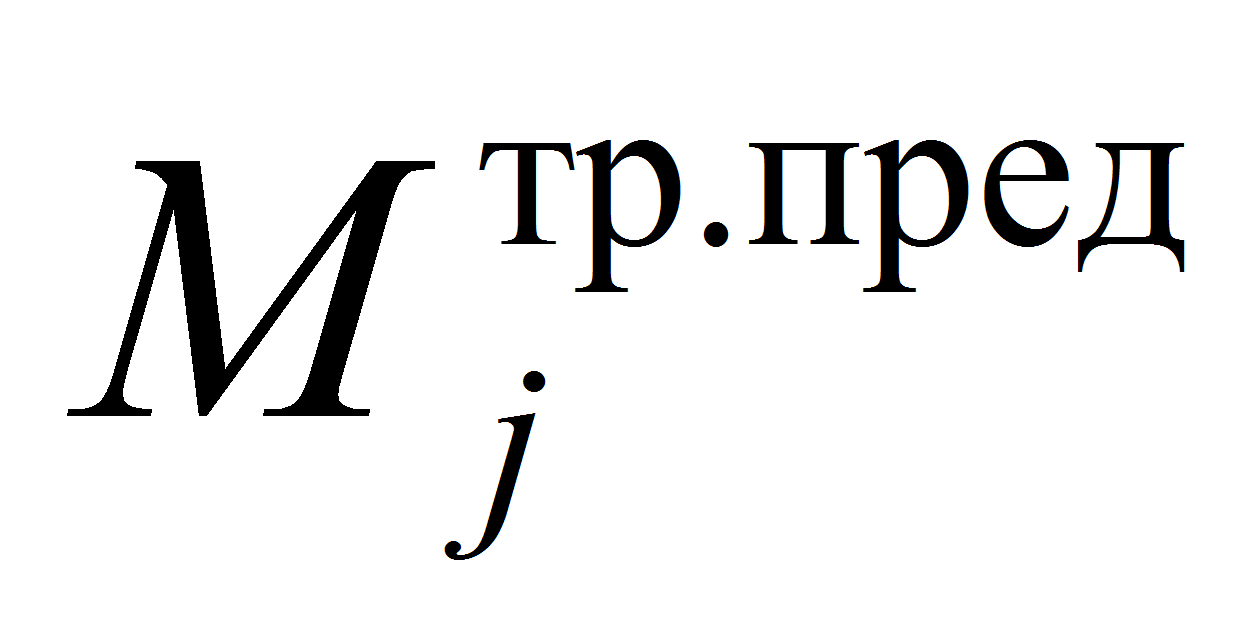 —
предельное значение силы трения, определяемая действующими силами
в шарнире и коэффициентом силы трения, в данном
случае, может быть определена экспериментально, для конкретно
взятого привода;
—
предельное значение силы трения, определяемая действующими силами
в шарнире и коэффициентом силы трения, в данном
случае, может быть определена экспериментально, для конкретно
взятого привода;
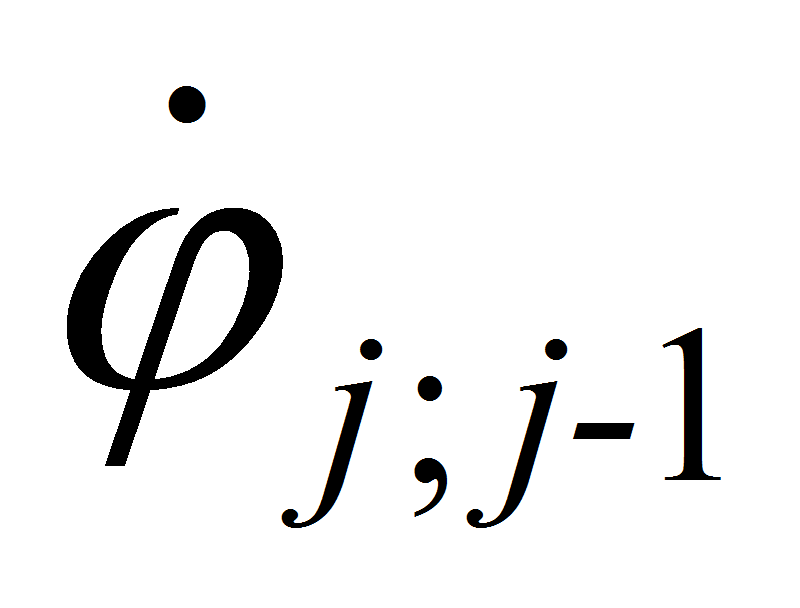 —
относительная скорость вращения между j-тым
и j-1
звеньями. Для получения численного решения систем уравнений (1–3),
был предложен оригинальный алгоритм интегрирования, позволяющий
моделировать движение робота.
—
относительная скорость вращения между j-тым
и j-1
звеньями. Для получения численного решения систем уравнений (1–3),
был предложен оригинальный алгоритм интегрирования, позволяющий
моделировать движение робота. -
Согласно принятому алгоритму
перемещения робота, существуют два этапа движения: удлинение корпуса
робота (при этом
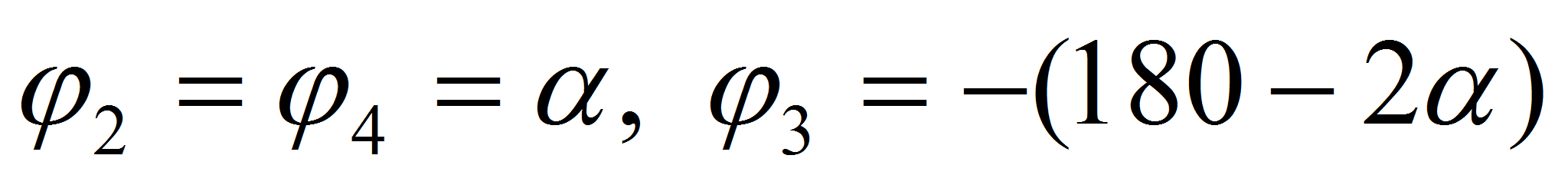 );
и сжатие корпуса робота (при этом
);
и сжатие корпуса робота (при этом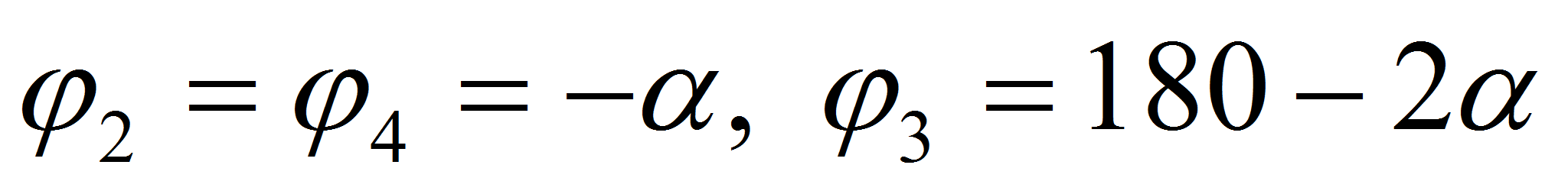 ),
где угол
),
где угол
 -
определяется как:
-
определяется как:
 ,
,
- где d — диаметр поперечного сечения трубы.
-
САУ формирует управляющее напряжение
Uj
для
двигателей в зависимости от задающих значений угла поворота
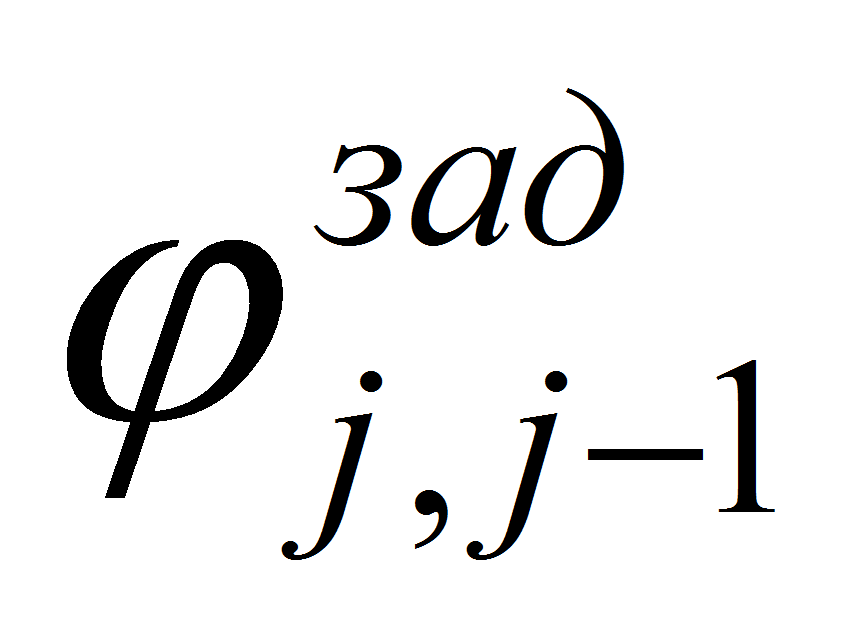 .
Задающие значения формируются в САУ в зависимости от
текущей конфигурации устройства и геометрии трубопровода.
Фактическое относительное перемещение звеньев
.
Задающие значения формируются в САУ в зависимости от
текущей конфигурации устройства и геометрии трубопровода.
Фактическое относительное перемещение звеньев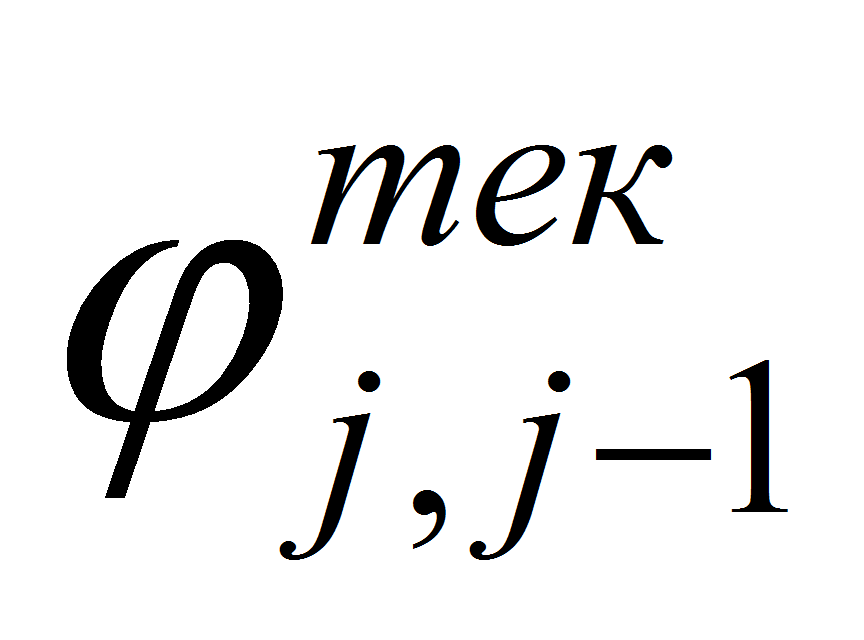 ,
фиксируется потенциометрическими датчиками угла поворота. Определяет
уровень управляющего напряжения:
,
фиксируется потенциометрическими датчиками угла поворота. Определяет
уровень управляющего напряжения:
|
(4) |
- Результаты моделирования движения робота. Моделирование проводилось при следующих исходных параметрах системы (табл. 1).
- Таблица 1
|
Наименование параметра |
Обозначение |
Единица измерения |
Значение |
|
Массы звеньев |
mj |
кг |
0,05 |
|
Длины звеньев |
lj |
м |
0,1 |
|
Предельный момент силы трения в шарнире* |
Нм |
0,0005 | |
|
Вязкое сопротивление в шарнире* |
- |
0,1 | |
|
Индуктивность цепи якоря** |
Гн |
0,0003 | |
|
Активное сопротивление якоря* |
rя,j |
Ом |
5,4 |
|
Электрическая постоянная времени электродвигателя** |
- |
0,005 | |
|
Моментный коэффициент электродвигателя** |
- |
1,5 | |
|
Передаточное число редуктора |
- |
50 | |
|
КПД привода |
- |
0,6 | |
| |||
- В процессе
моделирования значения углов:
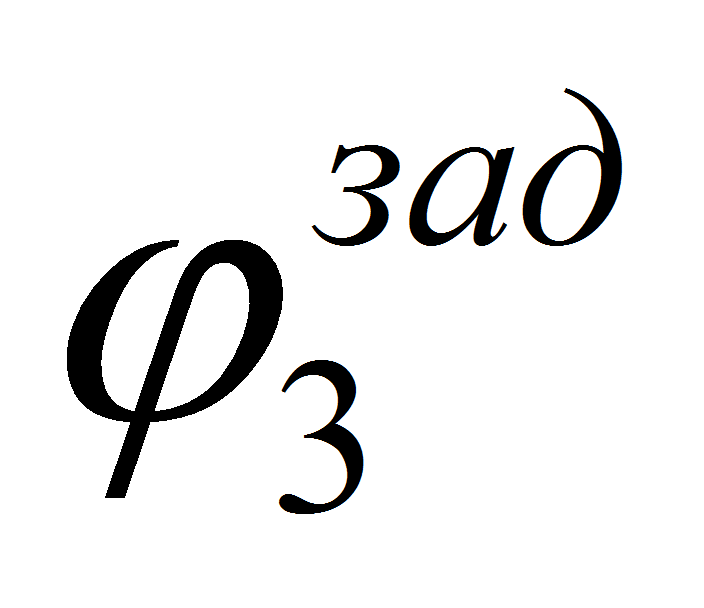 и
и
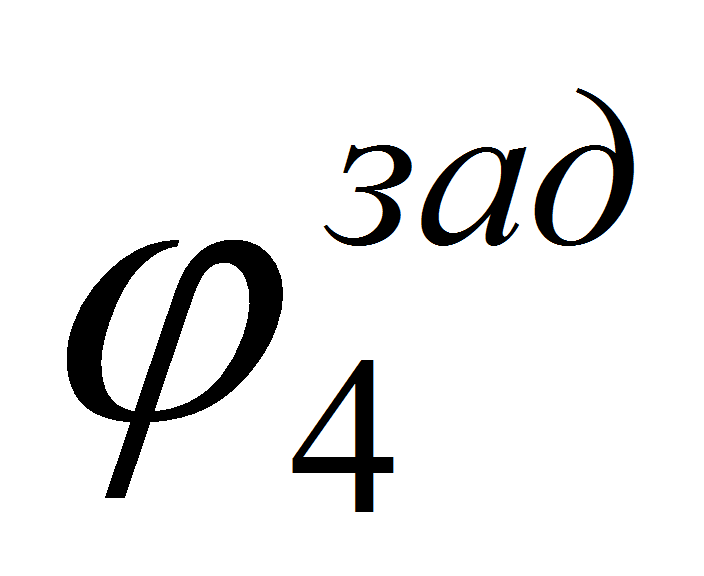 определялись следующим образом:
определялись следующим образом: -
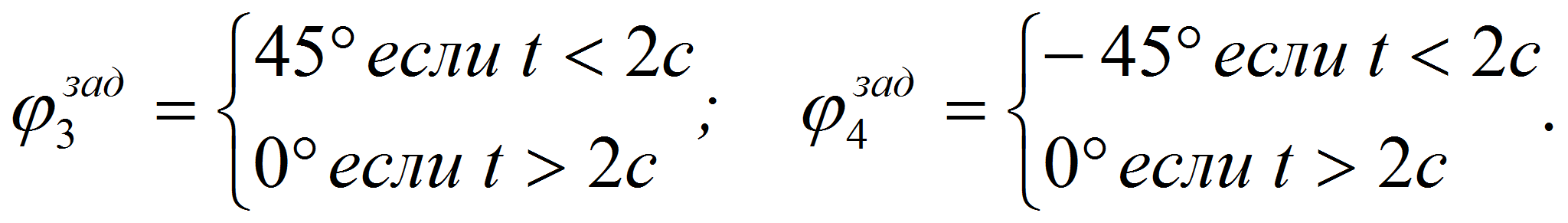
- Результаты математического моделирования представлены в виде временных диаграмм (рис. 3–5).
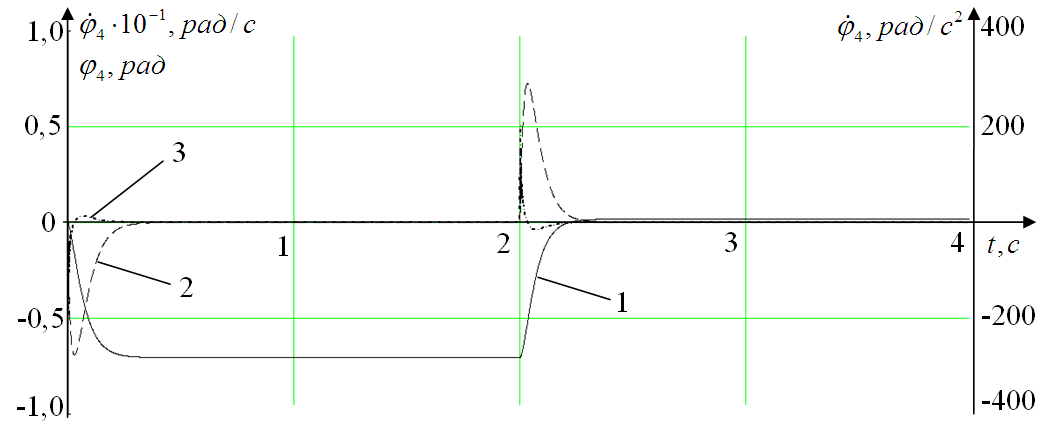
Рис. 3. Параметры перемещения 3-го звеньев робота. 1 — перемещение, 2 — угловая скорость, 3 — угловое ускорение
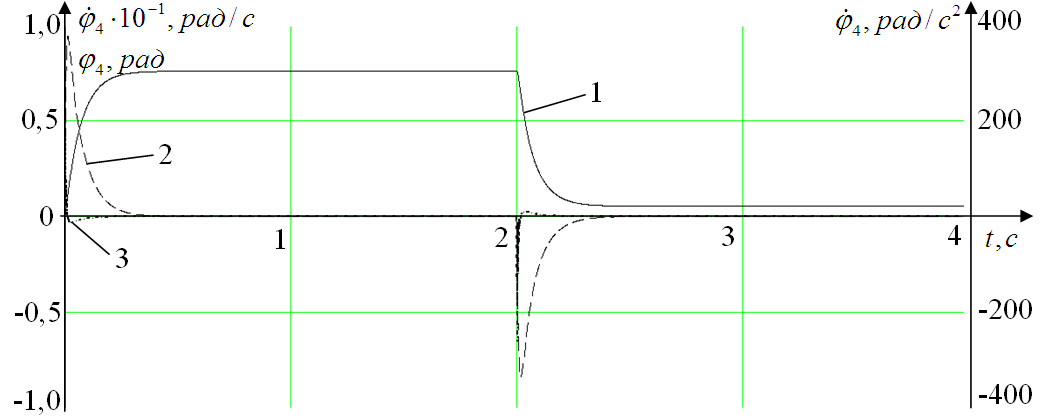
Рис. 4. Параметры перемещения 4-го звеньев робота .1 — перемещение, 2 — угловая скорость, 3 — угловое ускорение
-
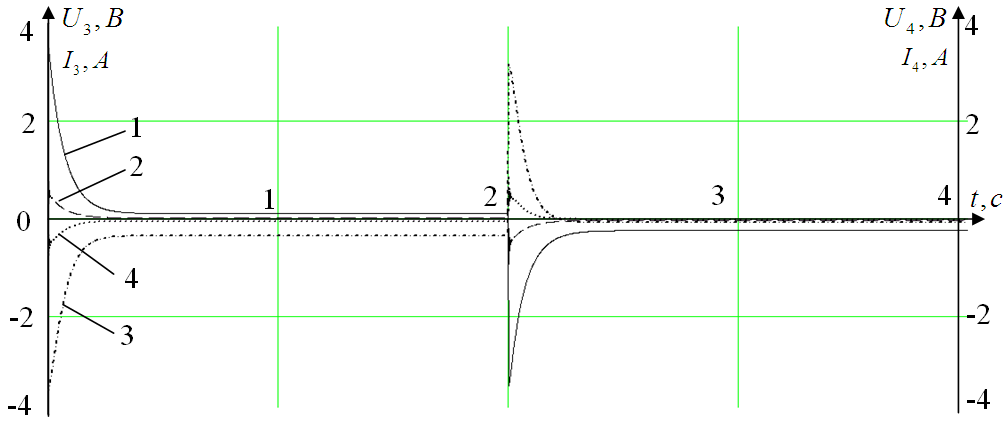
- На рис.5. показаны временные диаграммы, характеризующие изменение электрических параметров электродвигателей в процессе перемещения звеньев робота.
Рис. 5. Параметры энергопотребления приводов робота. 1 — напряжение на 3-ем приводе, 2 — ток на 3-ем приводе, 3 — напряжение на 4-ем приводе, 4 — ток на 4-ем приводе
-
- Выводы. В работе представлена математическая модель движения мобильного робота. Предложен оригинальный алгоритм, численного решения системы для уравнений, описывающих механические и электромеханические эффекты, возникающие в процессе движения звеньев. Математическое моделирование позволило получить закономерности изменения динамических параметров звеньев робота, для различных параметров САУ электроприводов. Установлено, что время перехода звена в заданное положение составляет в среднем 400мс, при этом развиваемые угловые скорости достигают значений 8 с-1, а угловые ускорения до 250 с-2. Управляющее напряжение, в процессе перемещения, не превышает номинального значения, равного 4.8 В. Пиковое значение тока в обмотках электродвигателя кратковременно достигает значения 0.5А, однако в среднем значение оценивается как 70мА, что соответствует номинальному току для данного типа приводов.
-
- Литература:
- Veshnikov V., Gradetsky V., Chaschuhin V. Computer modeling of the crawling robot motion inside a pipeline. // Proceedings of the 4-th International Workshop on Computer Science and Information Technologies CSIT — 02, Patras, Greece, September 18–20, 2002.
- E.Gambao, M. Hernando and A. Brunete,Multiconfigurable Inspection Robots for Low Diameter Canalizations, ISARC 2005 — September 11–14, 2005
- 3. Болотник Н. Н., Костин Г. В., Черноусько Ф. Л. Движение шагающего аппарата в тороидальной трубе // Изв. РАН. Механика твердого тела, 1998, № 4, с. 86–101
- Jatsun S., Zimmerman K., Zeigis I., Jatsun A. “Vibration driven robots for in pipe inspection”, Proceedings of International Conference on Mechatronics. Kumamoto, 2007, pp. 237–249.
- Мальчиков А. В., Математическое моделирование адаптивного внутритрубного робота // XXIII Международная инновационно-ориентированная конф. молодых ученых и студентов: мат. конф. — Москва ИМАШ РАН, 2011. С. 117.
- Мальчиков А. В., Адаптивный робот для перемещения по трубопроводам переменного диаметра, «Мехатроника, робототехника: современное состояние и тенденции развития» сб. науч. ст. Всерос. науч. школы для молодежи// ЮЗГУ, Курск, 2011, С. 110–118
- Мальчиков А. В., Автоматизированный мобильный комплекс для диагностики трубопроводов переменного диаметра, / А. В. Мальчиков, С. Ф. Яцун, Автоматизация и современные технологии, № 12. М, 2012. — С 3–8
- Мальчиков А. В. Динамические опорные элементы ползающих роботов для движения по наклонным поверхностям/ А. В. Мальчиков, С. Ф. Яцун, А. И. Жакин/ Известия Юго-Западного государственного университета, № 2 (41). Ч.1. Курск, 2012. С.89–95