Моделирование линейного асинхронного двигателя с укладкой обмотки индуктора (Z1 = 18) через спинку ярма

В работах [1] … [3] рассмотрено математическое моделирование линейных асинхронных двигателей при помощи магнитных схем замещения с классическим типом обмотки. В данной работе представлена математическая модель линейного асинхронного двигателя с намоткой обмотки через спинку ярма индуктора. Такой тип укладки обмотки позволит управлять напряжением в проводниках каждого паза и, кроме того, приводит к существенному изменению конфигурации заполнения элементов матриц [4]. Работа адресована студентам, поэтому дана без сокращений.

На рис.2,а показан линейный асинхронный двигатель с одной парой полюсов 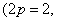 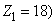с укладкой обмотки через спинку ярма статора. На рис. 2,б дана его магнитная схема замещения.

Запишем основные уравнения для «n»-ого участка схемы замещения.

Баланс магнитных напряжений магнитной цепи

Рис.1. Магнитная схема замещения

 Рис.2. а) Линейный асинхронный двигатель (2р = 2, Z1 = 18) б) Магнитная схема замещения

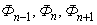 — контурные магнитные потоки;

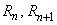 — магнитные сопротивления воздушных участков;

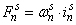 — магнитодвижущая сила, созданная статорным током 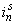, протекающим по всем проводникам паза ();

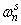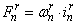 — М. Д. С. тока ротора в стержне ();

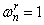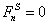– в шунтирующих зонах.

Баланс М. Д. С. для «n»-го участка имеет следующий вид:

.

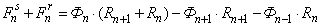Отсюда ток в стержне ротора определится по следующему выражению:

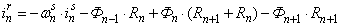                                                  (1)

Уравнение баланса напряжений электрической цепи ротора

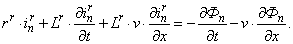                                                              (2)

Выразим производные во времени через конечные разности:

,

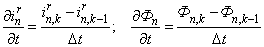где      n — номер зубцового деления;

k — номер шага разбиения по времени.

В формуле (2) скорость подвижного элемента принимаем равным 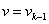 и в пределах «k» интервала считается постоянным.

Производные по пространственной координате «х» выразим через центральные конечные разности:

.

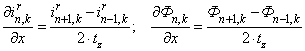С учетом вышеприведенных замечаний уравнение (2) примет следующий вид:

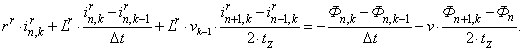                (3)

Исключим из уравнения (3) токи в роторе. Для этого подставим выражение (1) в уравнение (3) и получим:

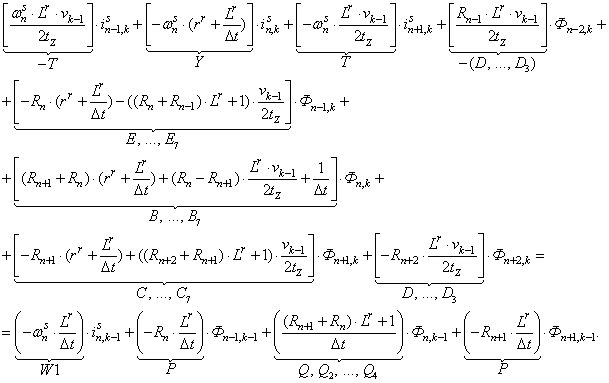(4)

Это уравнение может быть реализовано при произведении матрицы А, элементы которой записаны в квадратных скобках, на матрицу-столбец X, состоящей из потоков (Ф) и токов статорной обмотки. Правая часть уравнения (4) формирует первые двадцать шесть элементов матрицы-столбца свободных членовS в (k-1) момент времени. Остальные восемнадцать будут сформированы из баланса напряжений статорной обмотки.

Матрица-столбец Х сформирована из первых двадцати шести элементов, соответствующих потокам 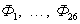, а с 27 по 44 — токам статорной обмотки i^s₁, …, i^s₁₈.

Общий вид матриц при числе полюсов 2р = 2 и общем числе пазов индуктора (статора) Z₁ = 18 приведен на рис.3.

Введем следующие обозначения:

-     Магнитные сопротивления в шунтирующих зонах:

R₁ = R₂ = R₂₆ = R₂₇ = 500 ∙ R_δ;

R₃ = R₂₅ = 50 ∙ R_δ;

R₄ = R₂₄ = 5 ∙ R_δ.

-     Магнитные сопротивления в индукторной зоне:

R₅ = R₆ = … = R₂₃ = R_δ.

-                  Элементы матрицы А, перемножаемые на потоки матрицы-столбца Х:

Рис. 3. Общий вид матриц A, X и S

  

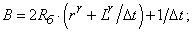
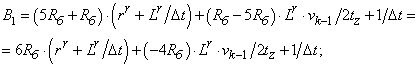
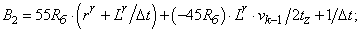
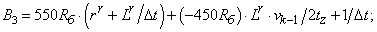
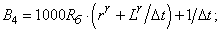
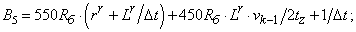
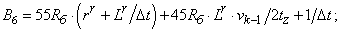
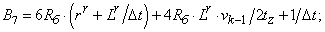
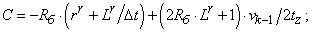
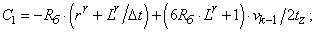
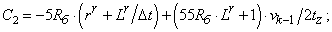
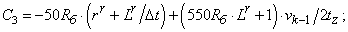
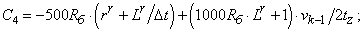
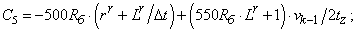
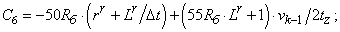
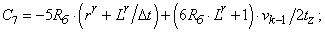
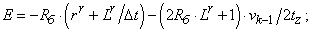
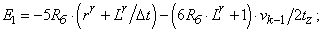
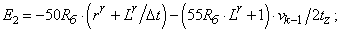
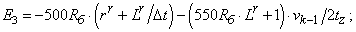
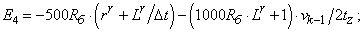
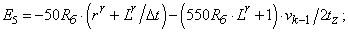
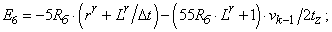
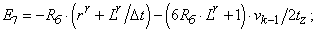
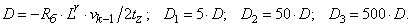
-                  Элементы матрицы А, перемножаемые на токи матрицы Х:

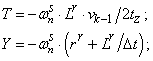
-                  Элементы матрицы-столбца свободных членов S:

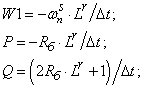
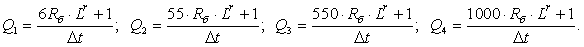Уравнение (4) позволит определить для первых двадцати шести строк элементы матрицы А и с первый по двадцать шестой элементы матрицы-столбца S, для этого последовательно зададимся n:

n = 1.

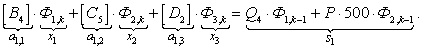
Запишем элементы матрицы А:

  

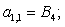
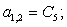
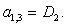
В правой части сформирован элемент 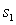 матрицы-столбца S:

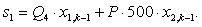
Примечание: вначале матрица А предстанет «пустой» и после каждой операции 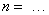 определятся постепенно элементы для каждой строки и только в конце всех операций матрица А предстанет перед читателем в том виде как она дана на рис. 3. Но эта «пустая» матрица А уже должна быть подготовлена. Эта «пустая» форма направляет, выступает «организующим началом» по поиску элементов в каждой строке.

При n = 1, как было показано выше, определились элементы первой строки. Найденные коэффициенты вписываем в матрицу А. В дальнейшем становится понятным алгоритм заполнения матрицы.

n = 2.

   

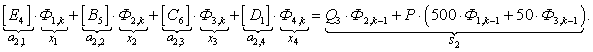
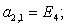
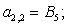
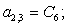
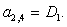
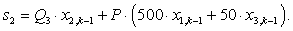
n = 3.

    

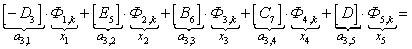
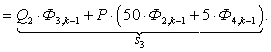
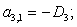
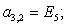
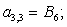
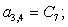
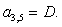
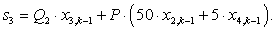
n = 4.

     

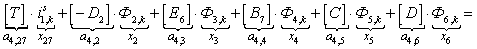
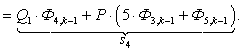
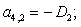
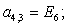
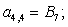
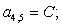
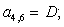
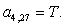
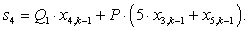
n = 5.

      

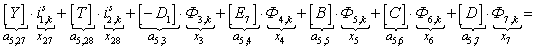
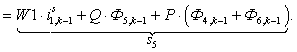
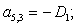
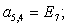
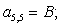
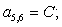
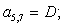
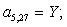
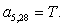
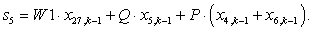
n = 6.

       

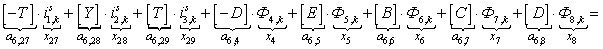
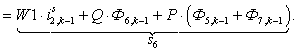
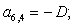
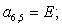
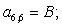
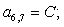
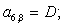
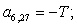
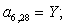
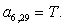
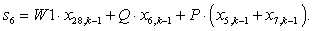
n = 7.

       

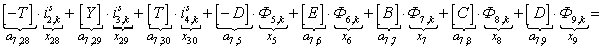
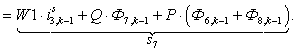
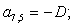
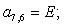
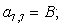
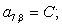
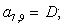
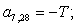
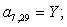
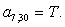
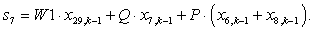
n = 8.

       

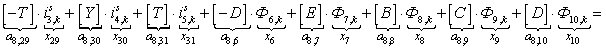
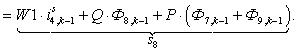
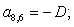
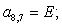
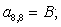
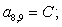
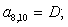
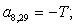
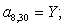
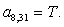
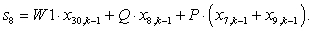
n = 9.

       

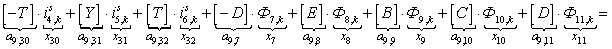
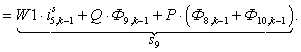
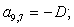
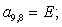
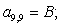
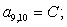
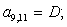
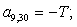
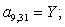
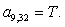
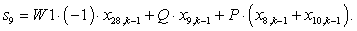
n = 10.

       

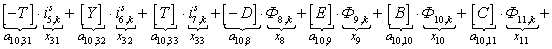
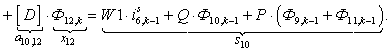
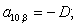
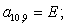
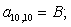
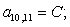
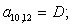
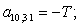
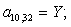
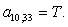
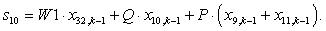
n = 11.

       

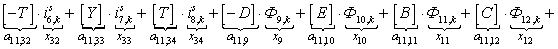
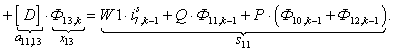
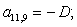
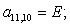
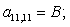
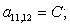
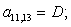
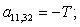
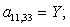
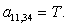
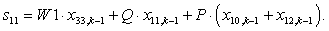
n = 12.

       

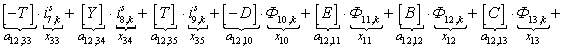
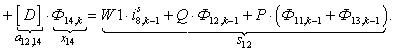
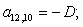
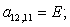
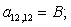
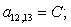
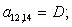
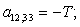
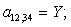
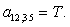
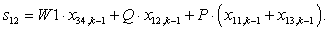
n = 13.

       

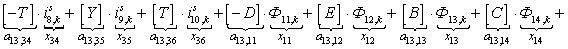
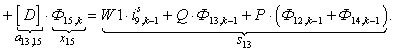
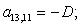
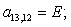
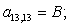
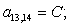
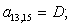
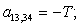
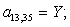
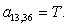
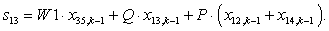
n = 14.

       

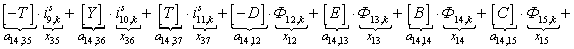
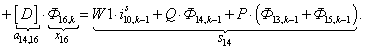
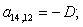
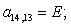
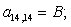
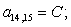
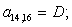
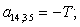
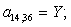
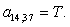
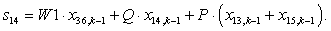
n = 15.

       

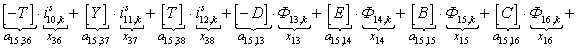
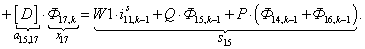
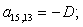
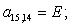
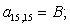
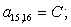
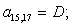
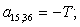
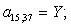
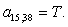
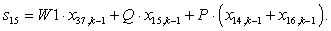
n = 16.

       

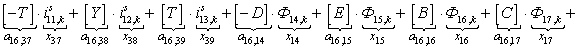
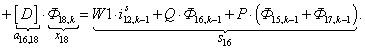
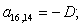
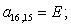
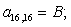
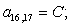
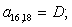
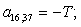
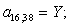
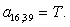
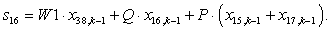
n = 17.

       

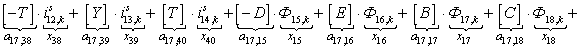
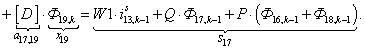
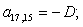
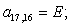
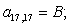
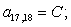
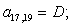
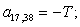
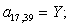
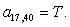
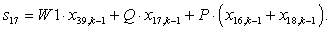
n = 18.

       

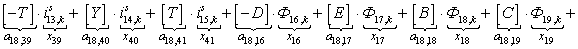
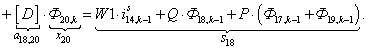
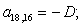
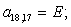
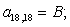
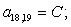
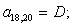
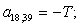
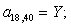
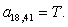
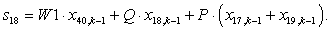
n = 19.

       

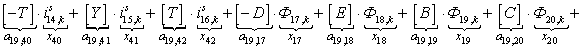
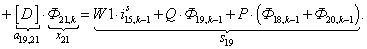
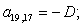
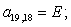
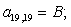
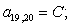
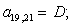
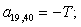
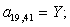
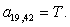
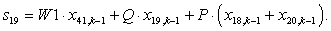
n = 20.

       

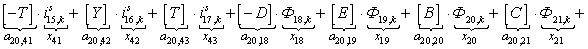
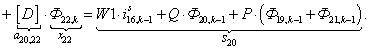
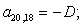
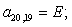
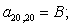
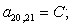
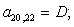
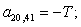
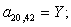
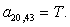
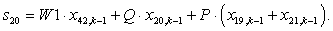
n = 21.

       

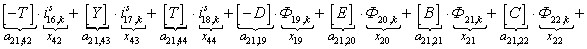
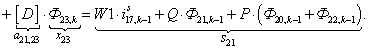
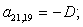
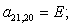
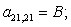
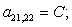
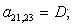
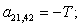
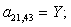
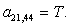
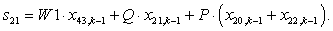
n = 22.

      

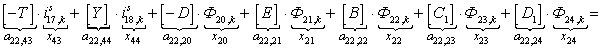
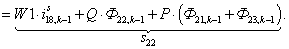
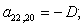
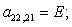
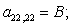
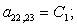
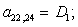
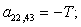
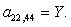
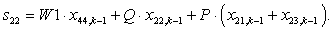
n = 23.

     

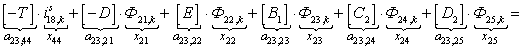
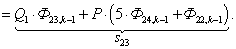
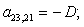
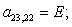
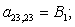
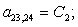
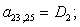
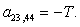
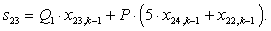
n = 24.

    

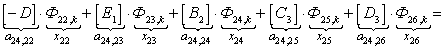
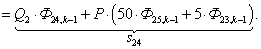
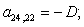
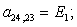
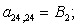
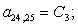
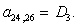
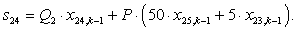
n = 25.

   

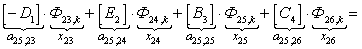
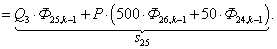
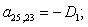
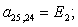
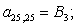
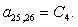
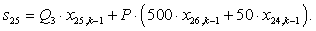
n = 26.

  

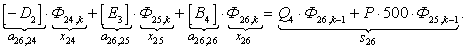
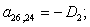
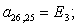
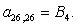
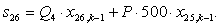
Остальные элементы матрицы А (n = 27, …, 44) и соответствующие элементы матрицы-столбца S определяются из баланса электрических напряжений обмоток статора [2].

В данной работе принято управление напряжением обмотки каждого паза 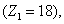 следовательно, необходимо задать восемнадцать напряжений. В качестве одного из вариантов примем синусоидальные напряжения со сдвигом на π/9:

                              

                   

                 

                 

              

              

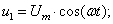
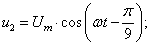
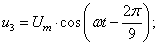
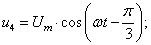
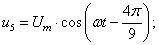
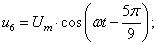
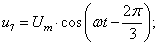
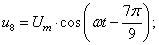
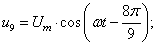
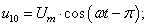
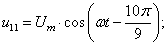
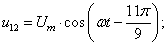
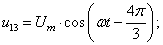
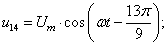
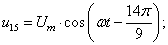
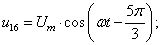
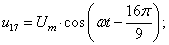
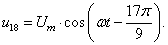
Рассмотрим баланс напряжений для первой обмотки.

,

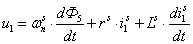где 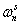      — число витков паза (обмотки);

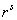 — сопротивление обмотки, проходящей через спинку ярма;

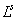– индуктивность обмотки первого паза.

Выразим производные через конечные разности:

;         .

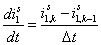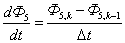Тогда после подстановки получим:

.

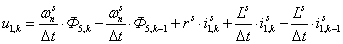Преобразуем выражение к виду:

.

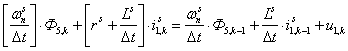Обозначим:

;       .

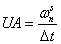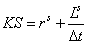Тогда для элементов двадцать седьмой строки матрицы А и двадцать седьмого элемента матрицы-столбца S (n = 27):

.

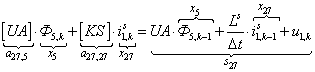Отсюда элементы матрицы А: ; .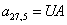

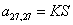Двадцать седьмой элемент 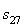 матрицы-столбца S:

.

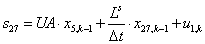Аналогично для n = 28, …, 44 запишем:

n = 28.          .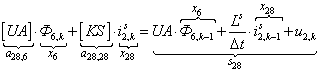

;  

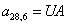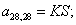
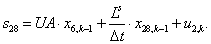
n = 29.          .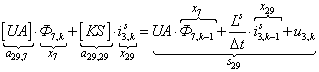

  

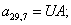
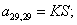
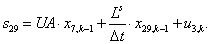
n = 30.          .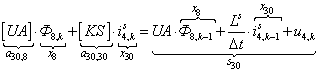

  

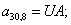
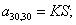
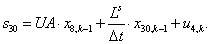
n = 31.          .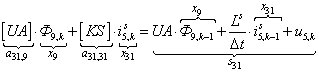

  

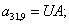
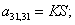
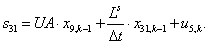
n = 32.          .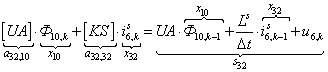

  

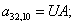
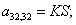
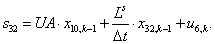
n = 33.          .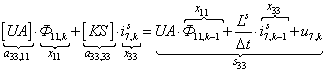

  

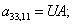
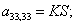
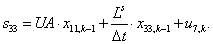
n = 34.          .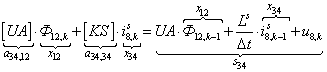

  

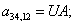
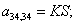
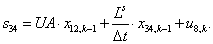
n = 35.          .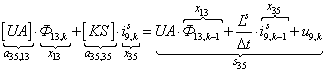

  

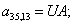
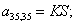
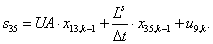
n = 36.          .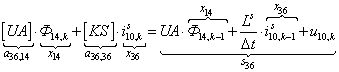

  

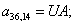
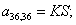
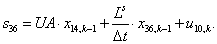
n = 37.          .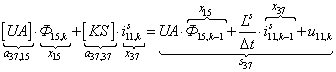

  

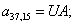
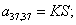
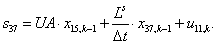
n = 38.          .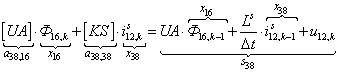

  

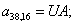
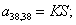
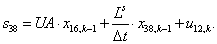
n = 39.          .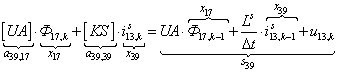

  

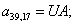
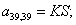
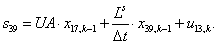
n = 40.          .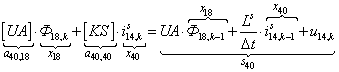

  

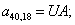
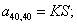
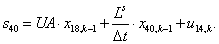
n = 41.          .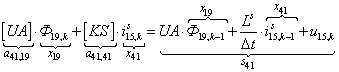

  

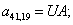
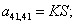
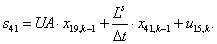
n = 42.          .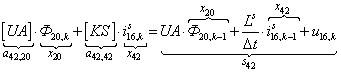

  

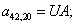
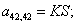
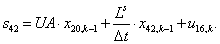
n = 43.          .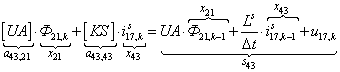

  

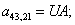
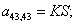
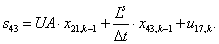
n = 44.          .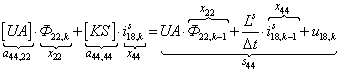

  

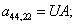
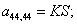
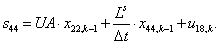
Окончательно, матрица А примет следующий вид, удобный для программирования в MATLAB:

Рис. 4

Неизвестные переменные (потоки и токи в статорной обмотке) в k-й момент времени определяются в результате следующей операции с матрицами:

X=A^-1·S,

Далее, подставляя в уравнение (1) n = 1…26, определяем токи в роторе:

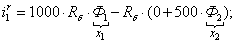
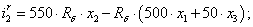
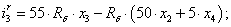
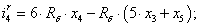
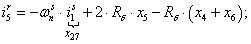
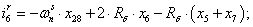
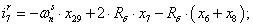
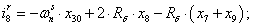
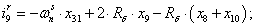
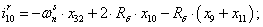
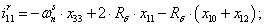
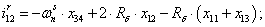
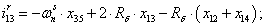
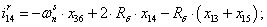
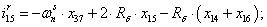
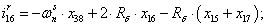
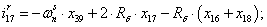
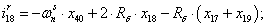
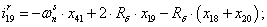
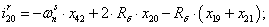
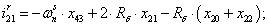
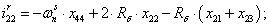
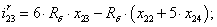
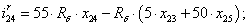
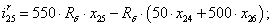
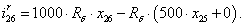
Электромагнитные усилия на зубцовом делении определяются по следующим формулам:

                                   

                             

                       

                  

                 

                 

    

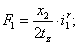
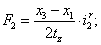
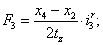
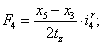
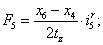
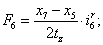
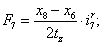
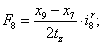
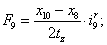
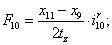
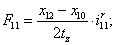
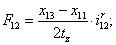
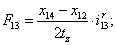
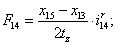
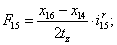
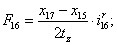
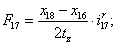
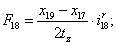
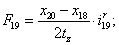
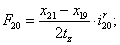
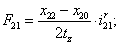
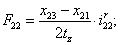
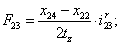
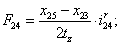
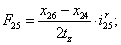
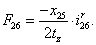
Суммарное усилие: .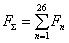

Скорость в k-й момент времени: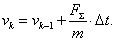

Произведем построение математической модели асинхронного двигателя методом Гаусса-Жордана с использованием языка программирования MATLAB. Ниже приведен пример кода.

% Математическая модель ЛАД с укладкой статорной обмотки через спинку

% ярма (Z1=18) c помощью магнитных схем замещения

  function LAD_Z1_18_spin

% Начальные условия

  Rb=(0.1003*10^7)*1;

  rs=5;

  Ls=0.02;

  rr=2.3*10^-5;

  Lr=0.06*10^-5;

  dt=0.001;

  tz=9.769*10^-3;

  m=3.8;

  v0=0;

  wn=200;

  f=50;

  w=2*pi*f;

  UA=wn/dt;

  Um=310/3;

  X=zeros(44,1);

  F=0;

  K=input('длительность цикла k=');

  for k=1:(K+1)

            v(1,k)=v0;     % создание вектора-строки для графика скорости

            f(1,k)=sum(F); % создание вектора-строки для графика усилия

            U(1)=Um*cos(w*(k-1)*dt);

            U(2)=Um*cos(w*(k-1)*dt-pi/9);

            U(3)=Um*cos(w*(k-1)*dt-2*pi/9);

            U(4)=Um*cos(w*(k-1)*dt-pi/3);

            U(5)=Um*cos(w*(k-1)*dt-4*pi/9);

            U(6)=Um*cos(w*(k-1)*dt-5*pi/9);

            U(7)=Um*cos(w*(k-1)*dt-2*pi/3);

            U(8)=Um*cos(w*(k-1)*dt-7*pi/9);

            U(9)=Um*cos(w*(k-1)*dt-8*pi/9);

            U(10)=Um*cos(w*(k-1)*dt-pi);

            U(11)=Um*cos(w*(k-1)*dt-10*pi/9);

            U(12)=Um*cos(w*(k-1)*dt-11*pi/9);

            U(13)=Um*cos(w*(k-1)*dt-4*pi/3);

            U(14)=Um*cos(w*(k-1)*dt-13*pi/9);

            U(15)=Um*cos(w*(k-1)*dt-14*pi/9);

            U(16)=Um*cos(w*(k-1)*dt-5*pi/3);

            U(17)=Um*cos(w*(k-1)*dt-16*pi/9);

            U(18)=Um*cos(w*(k-1)*dt-17*pi/9);

i_1(1,k)=X(27);

            i_7(1,k)=X(33);

            i_13(1,k)=X(39);

% Формирование матрицы сопротивлений

  R=zeros(27,1);

  R(1,1)=500*Rb;

  R(2,1)=500*Rb;

  R(3,1)=50*Rb;

  R(4,1)=5*Rb;

for i=5:23

          R(i,1)=Rb;

end;

  R(24,1)=5*Rb;

  R(25,1)=50*Rb;

  R(26,1)=500*Rb;

  R(27,1)=500*Rb;

% Формирование матрицы А

        A=zeros(44);

  B=2*Rb*(rr+Lr/dt)+1/dt;

  B1=6*Rb*(rr+Lr/dt)+(-4*Rb)*Lr*v0/(2*tz)+1/dt;

  B2=55*Rb*(rr+Lr/dt)+(-45*Rb)*Lr*v0/(2*tz)+1/dt;

  B3=550*Rb*(rr+Lr/dt)+(-450*Rb)*Lr*v0/(2*tz)+1/dt;

  B4=1000*Rb*(rr+Lr/dt)+1/dt;

  B5=550*Rb*(rr+Lr/dt)+450*Rb*Lr*v0/(2*tz)+1/dt;

  B6=55*Rb*(rr+Lr/dt)+(45*Rb)*Lr*v0/(2*tz)+1/dt;

  B7=6*Rb*(rr+Lr/dt)+(4*Rb)*Lr*v0/(2*tz)+1/dt;

  C=-Rb*(rr+Lr/dt)+(2*Rb*Lr+1)*v0/(2*tz);

  C1=-Rb*(rr+Lr/dt)+(6*Rb*Lr+1)*v0/(2*tz);

  C2=-5*Rb*(rr+Lr/dt)+(55*Rb*Lr+1)*v0/(2*tz);

  C3=-50*Rb*(rr+Lr/dt)+(550*Rb*Lr+1)*v0/(2*tz);

  C4=-500*Rb*(rr+Lr/dt)+(1000*Rb*Lr+1)*v0/(2*tz);

  C5=-500*Rb*(rr+Lr/dt)+(550*Rb*Lr+1)*v0/(2*tz);

  C6=-50*Rb*(rr+Lr/dt)+(55*Rb*Lr+1)*v0/(2*tz);

  C7=-5*Rb*(rr+Lr/dt)+(6*Rb*Lr+1)*v0/(2*tz);

  D=-Rb*Lr*v0/(2*tz);

  D1=5*D;

  D2=50*D;

  D3=500*D;

  E=-Rb*(rr+Lr/dt)-(2*Rb*Lr+1)*v0/(2*tz);

  E1=-5*Rb*(rr+Lr/dt)-(6*Rb*Lr+1)*v0/(2*tz);

  E2=-50*Rb*(rr+Lr/dt)-(55*Rb*Lr+1)*v0/(2*tz);

  E3=-500*Rb*(rr+Lr/dt)-(550*Rb*Lr+1)*v0/(2*tz);

  E4=-500*Rb*(rr+Lr/dt)-(1000*Rb*Lr+1)*v0/(2*tz);

  E5=-50*Rb*(rr+Lr/dt)-(550*Rb*Lr+1)*v0/(2*tz);

  E6=-5*Rb*(rr+Lr/dt)-(55*Rb*Lr+1)*v0/(2*tz);

  E7=-Rb*(rr+Lr/dt)-(6*Rb*Lr+1)*v0/(2*tz);

  T=-wn*Lr*v0/(2*tz);

  Y=-wn*(rr+Lr/dt);

  W1=-wn*Lr/dt;

  P=-Rb*Lr/dt;

  Q=(2*Rb*Lr+1)/dt;

  KS=rs+Ls/dt;

  Q1=(6*Rb*Lr+1)/dt;

  Q2=(55*Rb*Lr+1)/dt;

  Q3=(550*Rb*Lr+1)/dt;

  Q4=(1000*Rb*Lr+1)/dt;

for n=1:18

          A(n+4,n+4)=B;

          A(n+5,n+4)=E;

          A(n+3,n+4)=C;

          A(n+3,n+26)=T;

          A(n+4,n+26)=Y;

          A(n+5,n+26)=-T;

          A(n+26,n+4)=UA;

          A(n+26,n+26)=KS;

end;

for n=1:19

          A(n+2,n+4)=D;

          A(n+5,n+3)=-D;

end;

    A(1,1)=B4;

    A(1,2)=C5;

    A(1,3)=D2;

          A(2,1)=E4;

          A(2,2)=B5;

          A(2,3)=C6;

          A(2,4)=D1;

          A(3,1)=-D3;

          A(3,2)=E5;

          A(3,3)=B6;

          A(3,4)=C7;

          A(4,2)=-D2;

          A(4,3)=E6;

          A(4,4)=B7;

          A(5,3)=-D1;

          A(5,4)=E7;

          A(22,23)=C1;

          A(22,24)=D1;

          A(23,23)=B1;

          A(23,24)=C2;

          A(23,25)=D2;

          A(24,23)=E1;

          A(24,24)=B2;

          A(24,25)=C3;

          A(24,26)=D3;

          A(25,23)=-D1;

          A(25,24)=E2;

          A(25,25)=B3;

          A(25,26)=C4;

          A(26,24)=-D2;

          A(26,25)=E3;

          A(26,26)=B4;

% Матрица свободных членов

        S=[      Q4*X(1)+P*(        500*X(2));             %1

                 Q3*X(2)+P*(500*X(1)+50*X(3));             %2

                 Q2*X(3)+P*(50*X(2)+5*X(4));               %3

                 Q1*X(4)+P*(5*X(3)+X(5));                        %4

        W1*X(27)+Q*X(5)+P*(X(4)+X(6));                     %5

        W1*X(28)+Q*X(6)+P*(X(5)+X(7));                     %6

        W1*X(29)+Q*X(7)+P*(X(6)+X(8));                     %7

        W1*X(30)+Q*X(8)+P*(X(7)+X(9));                     %8

        W1*X(31)+Q*X(9)+P*(X(8)+X(10));                    %9

        W1*X(32)+Q*X(10)+P*(X(9)+X(11));                   %10

        W1*X(33)+Q*X(11)+P*(X(10)+X(12));                        %11

        W1*X(34)+Q*X(12)+P*(X(11)+X(13));                        %12

        W1*X(35)+Q*X(13)+P*(X(12)+X(14));                        %13

        W1*X(36)+Q*X(14)+P*(X(13)+X(15));                        %14

        W1*X(37)+Q*X(15)+P*(X(14)+X(16));                        %15

        W1*X(38)+Q*X(16)+P*(X(15)+X(17));                        %16

        W1*X(39)+Q*X(17)+P*(X(16)+X(18));                        %17

        W1*X(40)+Q*X(18)+P*(X(17)+X(19));                        %18

        W1*X(41)+Q*X(19)+P*(X(18)+X(20));                        %19

        W1*X(42)+Q*X(20)+P*(X(19)+X(21));                        %20

        W1*X(43)+Q*X(21)+P*(X(20)+X(22));                        %21

        W1*X(44)+Q*X(22)+P*(X(21)+X(23));                        %22

                 Q1*X(23)+P*(X(22)+5*X(24));               %23

                 Q2*X(24)+P*(5*X(23)+50*X(25));                  %24

                 Q3*X(25)+P*(50*X(24)+500*X(26));          %25

                 Q4*X(26)+P*500*X(25);                     %26

        UA*X(5)+Ls/dt*X(27)+U(1);                          %27

        UA*X(6)+Ls/dt*X(28)+U(2);                          %28

        UA*X(7)+Ls/dt*X(29)+U(3);                          %29

        UA*X(8)+Ls/dt*X(30)+U(4);                          %30

        UA*X(9)+Ls/dt*X(31)+U(5);                          %31

        UA*X(10)+Ls/dt*X(32)+U(6);                         %32

        UA*X(11)+Ls/dt*X(33)+U(7);                         %33

        UA*X(12)+Ls/dt*X(34)+U(8);                         %34

        UA*X(13)+Ls/dt*X(35)+U(9);                         %35

        UA*X(14)+Ls/dt*X(36)+U(10);                        %36

        UA*X(15)+Ls/dt*X(37)+U(11);                        %37

        UA*X(16)+Ls/dt*X(38)+U(12);                        %38

        UA*X(17)+Ls/dt*X(39)+U(13);                        %39

        UA*X(18)+Ls/dt*X(40)+U(14);                        %40

        UA*X(19)+Ls/dt*X(41)+U(15);                        %41

        UA*X(20)+Ls/dt*X(42)+U(16);                        %42

        UA*X(21)+Ls/dt*X(43)+U(17);                        %43

        UA*X(22)+Ls/dt*X(44)+U(18)];                       %44

% Решение методом Гаусса-Жордана

  Z=rref([A S]);   % Приведение расширенной матрицы к треугольному виду

  X=Z(1:44,45:45); % Выделение последнего столбца из матрицы

% Ток в роторе

  Ir=[     1000*Rb*X(1)- Rb*(        500*X(2));            %1

                  550*Rb*X(2)- Rb*(500*X(1)+50*X(3));            %2

                   55*Rb*X(3)- Rb*(50*X(2)+5*X(4));        %3

                    6*Rb*X(4)- Rb*(5*X(3)+X(5));           %4

          -wn*X(27)+2*Rb*X(5)- Rb*(X(4)+X(6));             %5

          -wn*X(28)+2*Rb*X(6)- Rb*(X(5)+X(7));             %6

          -wn*X(29)+2*Rb*X(7)- Rb*(X(6)+X(8));             %7

          -wn*X(30)+2*Rb*X(8)- Rb*(X(7)+X(9));             %8

          -wn*X(31)+2*Rb*X(9)- Rb*(X(8)+X(10));                  %9

          -wn*X(32)+2*Rb*X(10)-Rb*(X(9)+X(11));                  %10

          -wn*X(33)+2*Rb*X(11)-Rb*(X(10)+X(12));           %11

          -wn*X(34)+2*Rb*X(12)-Rb*(X(11)+X(13));           %12

          -wn*X(35)+2*Rb*X(13)-Rb*(X(12)+X(14));           %13

          -wn*X(36)+2*Rb*X(14)-Rb*(X(13)+X(15));           %14

          -wn*X(37)+2*Rb*X(15)-Rb*(X(14)+X(16));           %15

          -wn*X(38)+2*Rb*X(16)-Rb*(X(15)+X(17));           %16

          -wn*X(39)+2*Rb*X(17)-Rb*(X(16)+X(18));           %17

          -wn*X(40)+2*Rb*X(18)-Rb*(X(17)+X(19));           %18

          -wn*X(41)+2*Rb*X(19)-Rb*(X(18)+X(20));           %19

          -wn*X(42)+2*Rb*X(20)-Rb*(X(19)+X(21));           %20

          -wn*X(43)+2*Rb*X(21)-Rb*(X(20)+X(22));           %21

          -wn*X(44)+2*Rb*X(22)-Rb*(X(21)+X(23));           %22

                    6*Rb*X(23)-Rb*(X(22)+5*X(24));         %23

                   55*Rb*X(24)-Rb*(5*X(23)+50*X(25));            %24

                  550*Rb*X(25)-Rb*(50*X(24)+500*X(26));    %25

                 1000*Rb*X(26)-Rb*(500*X(25))];                  %26

% Электромагнитное усилие

        F(1)=X(2)*Ir(1)/(2*tz);

        for n=1:24

            F(n+1)=(X(n+2)-X(n))*Ir(n+1)/(2*tz);

        end;

        F(26)=-X(25)*Ir(26)/(2*tz);

% Скорость

        v0=v0+(sum(F)/m)*dt;

  end;

% Построение графиков

  k=0:K;

  subplot(2,1,1);

  plot(k*dt,v);

  title('скорость');

  xlabel('t,c');

  ylabel('v,m/c');

  grid on;

  subplot(2,1,2);

  plot(k*dt,f);

  title('Электромагнитное усилие');

  xlabel('t,c');

  ylabel('F,H');

  grid on;

  end

Временные зависимости скорости и электромагнитного усилия линейного асинхронного двигателя в режиме прямого пуска, полученные на математической модели, представлены на рис.5.

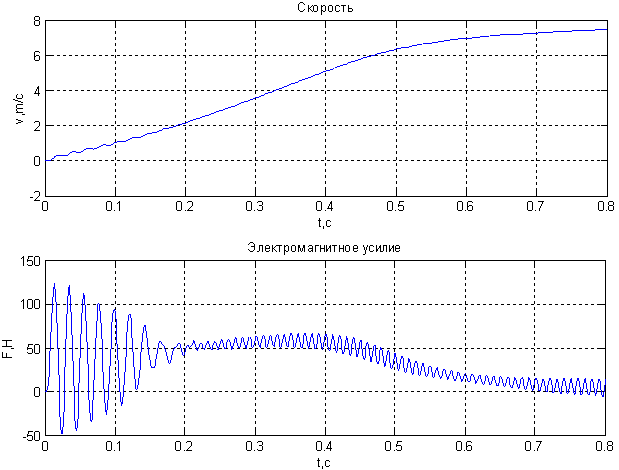
Рис.5. Результат моделирования линейного асинхронного двигателя в режиме прямого пуска

Зависимости токов даны на рис. 6 и 7.

Скорость

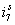
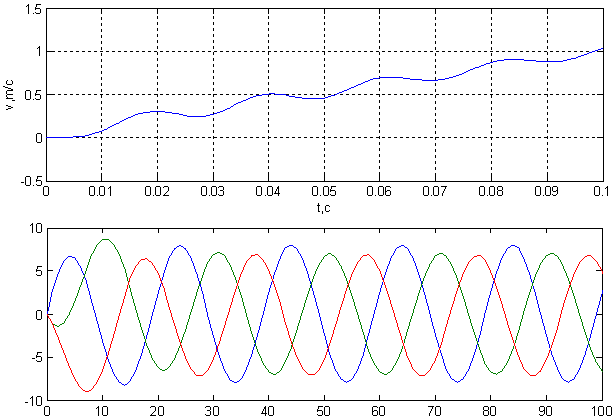
Рис. 6. Временные зависимост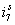и ,  и 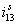при k = 100

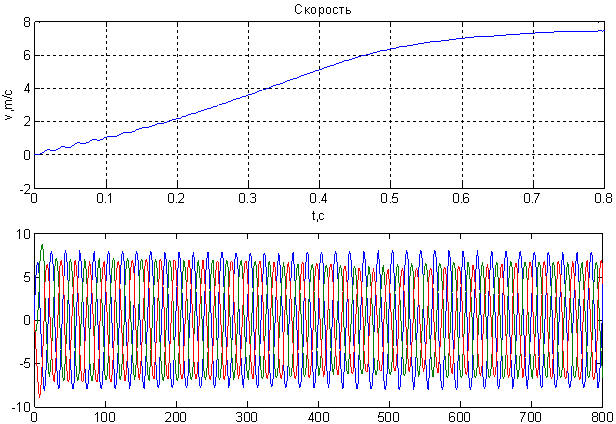
Рис. 7. Временные зависимост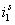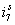и ,  и 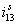при k = 800

Литература:

1.                  Емельянов А. А., Богатов Е. А., Клишин А. В., Медведев А. В., Симонович В. Г. Математическая модель линейного асинхронного двигателя на основе магнитных схем замещения // Молодой ученый. — 2010. — № 5. — С. 14–22.

2.                  Емельянов А. А., Медведев А. В., Богатов Е. А., Кобзев А. В., Бочкарев Ю. П. Программирование линейного асинхронного двигателя в MATLAB // Молодой ученый. — 2013. — № 3. — С. 129–143.        

3.                  Емельянов А. А., Медведев А. В., Кобзев А. В., Козлов А. М., Бесклеткин В. В., Бойко Д. Ю., Киряков Г. А., Чернов М. В., Королев О. А. Моделирование линейного асинхронного двигателя с укладкой обмотки индуктора (Z₁ = 12) через спинку ярма // Молодой ученый. — 2013. — № 8. — С. 13–31.

4.                  Емельянов А. А., Кобзев А. В., Козлов А. М., Бесклеткин В. В., Бочкарев Ю. П., Авдеев А. С., Киряков Г. А., Чернов М. В., Габзалилов Э. Ф. Программирование линейного асинхронного двигателя (Z₁ = 18) с трехфазной обмоткой индуктора с нулевым проводом // Молодой ученый. — 2014. — № 8. — С. 20–41.