Методические аспекты обучения младших школьников элементам математической статистики

Встатье рассмотрены методические аспекты формированияпрофессиональной компетентности будущего учителя начальной школы при обучении элементам математической статистики. Выявлены основные направления и особенности методики формирования первоначальных статистических представлений младших школьников.

Ключевые слова: профессиональная компетентность, стохастика, элементы математической статистики.

Внедрение элементов стохастики в курс математики средней школы в виде одной из сквозных содержательно-методических линий влечет за собой необходимость пропедевтической работы в начальной школе. Становится необходима профессиональная подготовка учителей начальных классов к формированию у младших школьников первоначальных стохастических представлений. Специфика реализации компетентностного подхода в педагогическом образовании состоит в том, что будущий учитель должен не только сам овладеть определенной компетентностью, но и быть готов к переносу своих навыков в сферу опыта учащихся для становления у них ключевых компетенций. В модели профессионального развития основной акцент переносится на становление умения видеть, осознавать и оценивать различные проблемы, конструктивно разрешать их в соответствии со своими ценностными ориентациями, рассматривать любую трудность как стимул к дальнейшему развитию. Система обучения стохастике направлена на познание окружающего мира средствами математики, общеинтеллектуальное, общекультурное развитие качеств мышления и качеств личности младшего школьника, необходимых для полноценного функционирования в современном обществе, для динамичной адаптации его к этому обществу, то есть на формирование у субъекта обучения в процессе изучения математики ключевых компетенций [1].

Изучение и анализ работы учителей по внедрению стохастической содержательно-методической линии в процесс обучения начальной школы позволяют сделать вывод, что основные причины трудностей кроются в недостатках их профессионально-педагогической подготовки [2, с.95].

Проблема исследования связана с выявлением теоретических и методических условий формирования профессиональной компетентности будущего учителя начальной − системы взаимосвязанных компонентов: фундаментальных предметных знаний, методических умений; профессионально-педагогических знаний и умений, профессионально значимых качеств личности учителя, которые реализуются в педагогической деятельности [3].

Эффективность подготовки учителей начальных классов в области формирования у младших школьников первоначальных стохастических представлений, будет достигнута, если подготовка построена на общих теоретических основаниях как система непрерывного образования, одной из целей которой является формирование профессиональной компетентности учителя начальных классов в указанной области [4]. Разработанная нами концептуальная модель формирования профессиональной компетентности студентов - будущих учителей начальной школы отражает характерные свойства, связи и отношения методической системы в доступной для анализа форме и обеспечивает переход теоретической сущности исследуемой проблемы в практическую действительность [5–7].

В содержании стохастической содержательно-методической линии выделяют три взаимосвязанных направления, методикой работы над которыми должен владеть будущий учитель: подготовка младших школьников в области комбинаторики, формирование первоначальных представлений о случайных событиях, формирование умений, связанных с представлением, сбором данных и их интерпретацией [8].

Статистическая составляющая заключается в сборе и анализе статистических данных, в ходе которых предусматривается ознакомление учащихся с простейшими способами регистрации и представления статистической информации, с возможностями ее использования для получения выводов об изучаемых явлениях. Она обеспечивает переход от реального мира к вероятностным моделям, связь их с реальной действительностью. Данная составляющая дает учащимся возможность развивать умение пользоваться статистическими показателями при выявлении общих тенденций и типичных свойств изучаемых явлений, анализировать данные, видеть конкретные явления с присущими им особенностями и причинными связями, обуславливающими наблюдаемые закономерности.

Целью изучения элементов математической статистики в начальной школе является формирование умений проводить несложные опросы, наблюдения с целью сбора количественной информации и ее оформления в виде таблиц, графиков, диаграмм; умений интерпретировать таблицы, схемы, графики, диаграммы.

К основным средствам формирования статистических представлений относят статистическое наблюдение и изображение получаемых сведений с помощью геометрических образов [8]. Статистическое наблюдение позволяет получить исходную информацию о некотором явлении или процессе. Графическое изображение полученных в результате наблюдений статистических сведений привлекает внимание, производит яркое и живое впечатление, становится более доходчивым и запоминающимся. Статистические таблицы и графики помогают осмыслить полученный материал, дают целостную картину изучаемого явления. В них становятся особенно наглядными и выразительными взаимные связи между явлениями, сравнительные характеристики и основные тенденции развития. Следовательно, роль графических изображений как средства обобщения и анализа статистических данных исключительно велика [8].

Одним из средств систематизации и обобщения полученных в наблюдениях статистических данных являются таблицы. Когда материал приведен в систему, определено относительное значение каждого признака, тогда уже можно выяснить, какие признаки совпадают, что именно характеризуют те или иные из них, тогда-то возможно определить, есть или нет порядок и последовательность между явлениями, сопровождается ли один признак другим, и если да, то каким, какая связь существует между различными явлениями, наблюдается ли существование или последовательность, и каких именно явлений, тогда появляется возможность сделать научные выводы [9, с. 74]. Использование табличной формы позволяет расположить данные компактно, наглядно и рационально, за счёт чего облегчается их анализ, вскрываются те или иные характерные особенности изучаемых явлений: сходство и различие, взаимосвязь признаков и т. п. Это достигается тем, что внутри таблицы сведения располагаются рядами и столбцами, что дает возможность охватить их взглядом и сравнить между собой.

Каждая правильно оформленная таблица содержит три основных элемента: заголовок, указывающий на цель или содержание таблицы, подлежащее, то есть перечень тех групп или частей, на которые подразделена вся масса единиц совокупности, сказуемое, то есть совокупность чисел, при помощи которых характеризуются выделенные в подлежащем группы.

При работе с таблицами в начальной школе следует отметить, что в самом простом случае таблица делится на строкиистолбцы. Обычно каждый столбец имеет название, которое указывается в первой строке таблицы. Важно проиллюстрировать учащимся разнообразные таблицы и попросить привести примеры. Примерами могут служить: страницы классного журнала, календарь, расписание уроков в школе и т. д. Цель рассмотрения подобных примеров — формирование у младших школьников представлений о том, что в жизни часто приходится сталкиваться с разнообразными таблицами, поэтому важно научиться пользоваться информацией помещенной в них и составлять их самим.

В процессе статистического наблюдения, если результаты записываются в том порядке, в котором они поступают, целесообразно составлять таблицу регистрации. Эта первичная таблица дает некоторое представление о связях, общих чертах и различиях получаемых статистических данных. В таблице исходных данных просматриваются не только объем совокупности, но и наиболее характерные ее черты: структура, типичные проявления, изменчивость признака и т. д. Представление о степени вариации однородных признаков дает простое сопоставление нескольких таблиц.

От таблицы исходных данных целесообразно перейти к таблице частот (относительных частот), если рассматривать числовые данные в порядке возрастания, построить таблицы накопленных частот. Любая из данных таблиц может быть как простой (в подлежащем ее нет группировок), так и групповой (изучаемый объект разделен в подлежащем на группы), как дискретной (в подлежащем имеются только отдельные, изолированные друг от друга значения признака), так и непрерывной (интервальной).

Приведем пример задания направленного на формирование умений и навыков работы с таблицами. Задание. Используя данные таблицы, ответьте на вопросы. На сколько граммов яблоко легче апельсина? На сколько граммов яблоко легче дыни? На сколько граммов яблоко тяжелее лимона? Чему равна масса 5 яблок? Что легче: 2 яблока или 3 лимона? На сколько масса арбуза больше массы дыни? Во сколько раз масса 4 апельсинов больше массы 2 яблок? Во сколько раз масса 4 апельсинов больше массы 4 яблок?

Фрукты	Количество	Масса
Яблоко	2 шт.	400 г
Лимон	4 шт.	600 г
Дыня	1 шт.	2 кг 200 г
Апельсин	4 шт.	800 г
Арбуз	1 шт.	3 кг 600 г

Система заданий, направленных на формирование умений работы со статистическими таблицами, должна включать задания, развивающие умения извлекать и анализировать информацию, представленную в таблице, вырабатывающие умения представлять необходимую информацию в виде таблицы.

Большинство учебников содержат лишь готовые таблицы для работы, поэтому можно предложить учащимся задания на составление таблиц по имеющимся данным. Например, предложить провести опрос среди одноклассников и друзей на разнообразные темы (как добираются до школы ученики вашего класса, какие кружки или секции посещают ваши одноклассники, какие домашние животные есть у них дома и т. д.) и полученные сведения представить в виде таблицы. Постепенно необходимо увеличивать трудность заданий: предлагать для анализа более обширные таблицы данных, по которым сложнее ориентироваться и, используя их, заполнять новые таблицы.

В настоящее время появилась тенденция к расширению спектра использования различных методов решения задач. При сравнении данных, с увеличением числа объектов, целесообразно использовать графические изображения, позволяющие упросить рассуждения. Доступным для учащихся средством графического изображения статистических данных являются диаграммы, дающие обобщающую картину взаимосвязей единиц статистической совокупности и способствующие выявлению закономерностей.

Столбчатая диаграмма - это совокупность прямоугольников в одной полуплоскости с основаниями, принадлежащими одной прямой, и высотами, характеризующими различные единицы статистической совокупности. Она помогает закрепить представления о событиях «более возможных» и «менее возможных», сформировать представление о равновозможных событиях, даёт представление как о дискретных распределениях, так и о непрерывных. Использование столбчатых диаграмм позволяет делать выводы о степени разброса значений.

К рассмотрению диаграмм целесообразно перейти после того, как у младших школьников выработаны навыки работы с таблицами. Если с таблицами младшие школьники встречались ранее, то понятие диаграммы может оказаться для них совершенно новым. Поэтому начинать знакомство учащихся с диаграммами разумнее с конкретного примера, иллюстрирующего, что такое диаграмма и для чего она нужна. Для этого можно рассмотреть, например, такую задачу.

Задача. Конфетная фабрика приняла заказ на изготовление партии из 2000 шоколадок. Каждая из шоколадок по плану должна весить 40 грамм. Но контрольное взвешивание изготовленной партии шоколада дало следующие результаты (результаты взвешивания представлены в виде таблицы):

Таблицы позволяют представить необходимую информацию в удобной для восприятия форме. Еще более удобным способом представления информации является графический, то есть на рисунках. Давайте внимательно посмотрим на рисунок 1, построенный по исходной таблице. Этот рисунок и называется диаграммой.

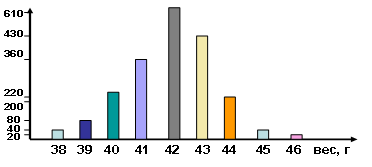
Рис. 1.

После этого нужно организовать работу учащихся с диаграммой для того, чтобы они смогли оценить достоинства представления данных таким способом. Целесообразно задать вопросы: «Шоколадок какого веса завод выпустил больше всего? Сколько шоколадок весом 39 граммов выпустил завод? Шоколадок какого веса завод выпустил меньше всего? Сколько шоколадок весом меньше 41 грамма произвел завод? И т. п».

Для формирования умений, связанных с использованием диаграмм, предлагаем следующие задания.

Задание.Дайте ответы на поставленные вопросы, используя диаграмму.

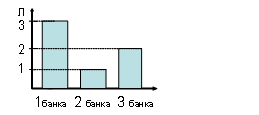
Рис. 2.

Сколько литров сока в большой и средней банках? Сколько литров сока в средней и маленькой банках? Сколько литров сока в трех банках? На сколько литров сока больше вошло в большую банку, чем в маленькую? На сколько литров сока в большой и маленькой банках вместе, больше, чем в средней?

Важно выработать у учащихся четкий алгоритм построения столбчатых (линейных) диаграмм: подобрать цену деления шкалы, удобную для обозначения на ней значений данных величин; изобразить шкалу на вертикальном координатном луче, а на горизонтальном луче отметить на равном расстоянии друг от друга точки по числу имеющихся величин; от выбранных точек построить вертикальные отрезки (столбцы), высота которых равна значению соответствующей величины.

Диаграмму, построенную таким способом, называют столбчатойдиаграммой, но если вместо столбиков изобразить линии той же высоты, получим новый вид диаграммы — линейную диаграмму. Далее целесообразно предложить учащимся построить несколько диаграмм для отработки шагов алгоритма с разбором у доски.

Статистическую информацию можно изображать с помощью круговой (секторной) диаграммы, которая представляет собой круг, разделенный на секторы с площадями, пропорциональными частотам. Круговые диаграммы показывают, прежде всего, состав статистической совокупности, ее структуру и располагают большими возможностями для ознакомления учащихся с начальными идеями так называемого метода Монте-Карло получения экспериментальных значений случайной величины.

Задача. Маша, Саша, Катя, Лена, Ваня и Миша пошли в пиццерию. На диаграмме показано, сколько кусков пиццы съел каждый из них. Ответьте на вопросы. Кто из ребят съел пиццы больше всех? Кто из ребят съел пиццы меньше всех? Кто из ребят съел одинаковое количество кусков пиццы? Сколько кусков пиццы вместе съели ребята? Сколько кусков пиццы съели вместе Маша, Лена и Катя?

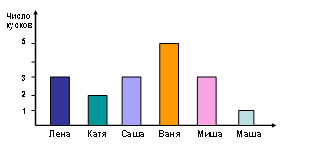
Рис. 3.

После того, как учащиеся справятся с этими заданиями, можно перейти к изучению круговых диаграмм. Необходимо продемонстрировать учащимся пример круговой диаграммы, которая может быть построена по таблице 3.

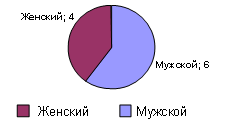
Рис. 4.

До этого вы строили столбчатые и линейные диаграммы, но существует еще один вид диаграмм — круговые диаграммы. Такая диаграмма представляет круг, разрезанный на дольки, каждая из долек соответствует одному из значений изучаемого признака (в нашем случае — пол ребенка), ее размер пропорционален интересующей нас величине (количеству новорожденных данного пола).

При изучении данной темы у учащихся должен быть сформирован четкий алгоритм построения круговых диаграмм: найти часть целого, которая приходится на каждую из величин; найти величины центральных углов, соответствующих каждой части;построить в данной окружности центральные углы, соответствующие каждой части.

Целесообразно предложить учащимся выполнить задания на построение круговых диаграмм по таблицам данных. Важно обратить внимание младших школьников на возможность взаимозаменяемости различных видов диаграмм. На вопрос учителя «Можно ли, глядя на столбчатую диаграмму, построить по ней линейную?» учащиеся без труда должны ответить «да», поскольку надо всего заменить столбики линиями соответствующей высоты. Значит, используя столбчатую диаграмму, можно построить линейную, и наоборот. Аналогично, из столбчатой или линейной диаграммы можно построить круговую, и наоборот. Для закрепления навыков нужно предложить школьникам задания, требующие построить диаграмму другого вида по имеющейся.

Для анализа динамики явленийудобны линейные статистические графики: на одном чертеже наносят несколько таких графиков и производят их сравнение. По графикам легко видеть не только то, насколько возрос тот или иной показатель, но и как это изменение связано со временем, за которое данное изменение произошло. Поэтому такие графики по праву можно считать содержательным компонентом формирования первоначальных представлений о случайных явлениях и процессах.

Задание. На рисунке 5 дан график движения велосипедиста. Пользуясь графиком, ответьте на вопросы.

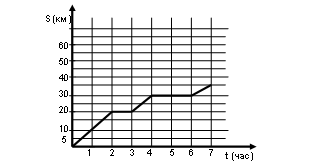
Рис. 5.

Сколько километров проехал велосипедист: за первый час движения; за третий час движения; через два часа после выезда; через 5 часов после выезда? Сколько времени затратил велосипедист на весь путь? За сколько часов он проехал 10 км, 20 км,35 км? Сколько раз велосипедист отдыхал? Сколько времени велосипедист отдыхал? Вычислите, с какой скоростью ехал велосипедист до остановки. Вычислите, с какой скоростью ехал велосипедист после второй остановки.

Ценность заданий стохастического характера определяется не только тем аппаратом, который используется при их решении, но и возможностями продемонстрировать процесс применения математики для решения практических проблем. Стохастические задачи, знакомящие младших школьников со сферой случайных событий и формирующие у них первоначальные статистические представления, способствуют познанию окружающего мира средствами математики. Статистическая составляющая дает возможность сравнивать совокупности данных по степени их вариации, помогая пониманию изменчивости, скрывающейся за средними показателями. Количественная оценка степени вариации потребуется выпускнику школы для простейшего сравнения производственных показателей, правильному осмыслению происходящих в окружающей жизни событий.

Анализ статистических данных постепенно убеждает учащихся, что собранный материал рассматривается не ради него самого, а лишь как некоторая пробная группа, представляющая только один из возможных вариантов исследования. На основании результатов наблюдений или измерений они учатся делать выводы относительно более широкого круга явлений. Так они начинают познавать основные идеи и понятия выборочного метода и учатся в простейших случаях пользоваться им на практике.

Литература:

1.                  Проценко Е. А., Трофименко Ю. В. Методические аспекты обучения младших школьников стохастике. Молодой ученый. 2013. № 11. С. 633–637.

2.             Проценко Е. А., Трофименко Ю. В. Формирование профессиональной компетентности будущих учителей начальной школы при обучении стохастике. Вестник Таганрогского государственного педагогического института. 2013. № 1. С. 094–100.

3.                  Проценко, Е. А. Концептуальная модель формирования профессиональной компетентности будущих учителей начальной школы при обучении стохастике//Вопросы гуманитарных наук. -2008. -№ 3 (36). -С. 285–292.

4.                  Проценко, Е. А. Теоретические и методические основы изучения комбинаторики в начальной школе / Е. А. Проценко, Г. А. Семенова. -Таганрог: Изд-во Таганрог. гос. пед. ин-та, 2008. -128 с.

5.                  Проценко, Е. А. Использование информационных технологий как средства организации самостоятельной работы студентов//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. -2006. -№ S16. -С. 77–81.

6.                  Проценко, Е. А. Применение компьютерных средств обучения в процессе преподавания комбинаторики//Вестник Московского городского педагогического университета. -2006. -№ 6. -С. 167–170.

7.                  Проценко Е. А., Трофименко Ю. В. Методические аспекты обучения младших школьников комбинаторике. Молодой ученый. 2014. № 67. С. 633–637.

8.             Селютин В. Д. Научные основы методической готовности учителя математики к обучению школьников стохастике: Дис.... д-ра пед. наук. М., 2002.

9.                  Каблуков Н. А. Статистика: Теория и методы статистики. Основные моменты в истории ее развития 5-е изд.,стереотип. -М.: Центр.стат.упр., 1922.