Вопрос моделирования системы частотных характеристик барабанов не раскрыт полностью и может найти применение в разных областях, как имитационных, так и реальных. Исследование могут найти применение в музыкальной индустрии, упростив при этом точную настройку ударной установки под определенный запрос музыканта.
Ударная установка является системой, состоящей из подсистем имеющих множественную параметрическую базу. Один барабан, входящий в УУ, может производить звук с определённой функцией спектральной плотности зависящей от множества параметров, таких как сила удара, упругость материала, наличие резонансной мембраны, сила натяжения мембраны, которая в свою очередь определяется углом поворота крепёжных винтов обода барабана, и т. д.
Для снятия значений был выбран микрофон с широким частотным диапазоном, так как результирующий сигнал будет менее всего подвержен помехам. Приложение для работы с математической моделью позволяет упростить подход к математическим расчетам, автоматизируя процесс расчета.
Имеются два основных вида настройки барабанов: EVEN (равномерная) и ODD (неравномерная, разрозненная). EVEN настройка подходит для закрытых барабанов и является основой для последующего выполнения настройки ODD.
Мембрану необходимо натянуть равномерно. Каждый регулировочный болт должен притягивать мембрану к корпусу барабана с одинаковой силой. Первым делом закручиваются все имеющиеся болты пальцами до упора. Затем ключом закручивается на пол-оборота (на 90 градусов) ближайший болт, потом диаметрально противоположный болт и повторяются действия пока все болты не будут отрегулированы результате этих действий мембрана должна быть натянута равномерно, ноты должны быть одинаковыми.
Настройка рабочего барабана слегка отличается от настройки тома, т. к. ударная и резонансная мембраны рабочего барабана имеют разные толщины. Низкая настройка ударной мембраны дает глубокий, но статичный звук. Высокая настройка ударной мембраны дает звук сухой, живой и яркий. Низко настроенная резонансная мембрана рабочего барабана дает звук с основным тоном, доминирующим над звуком пружины, и соответственно, чем выше настраиваемая резонансная мембрана, тем более резким становится звук рабочего барабана. Также большое значение имеет толщина мембран. Тонкие мембраны имеют подчеркнутую атаку и долгое затухание, а звук более толстых и двойных мембран отличается быстрым затуханием.
В качестве студии звукозаписи выбираем Adobe Audition 3.0, в качестве программных средств MathCAD 14, в качестве аппаратных средств микшерный пульт Mackie CR 1604 VLZ с микрофоном кругового охвата.
После записи звука, в программе Adobe Audition 3.0 получаем вид сигнала на тайм линии. Выделяем пустую (не содержащую полезной информации) область сигнала для снятия показаний шума (Рисунок 1):
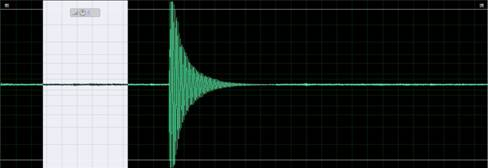
Рис. 1. Тайм линия с записанным звуком и шумом
После применения исключения шума из сигнала, можно выделить только область с полезной информацией (Рисунок 2), после чего файл сохраняется и осуществляется поворот всех винтов на 90о, после чего замеры повторяются.
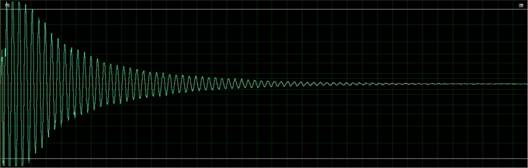
Рис. 2. Полезная информация
После получения полезного сигнала проводится частотный анализ, для этого программное средство переводится в соответствующий режим. После чего в анализатор передаются параметр по количеству точек БПФ: 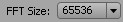 И на тайм панели выделяется вся область сигнала. В анализаторе запускается анализ (Scan Selection). Полученный результат является спектральной плотностью полученной программно.
И на тайм панели выделяется вся область сигнала. В анализаторе запускается анализ (Scan Selection). Полученный результат является спектральной плотностью полученной программно.
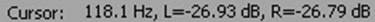
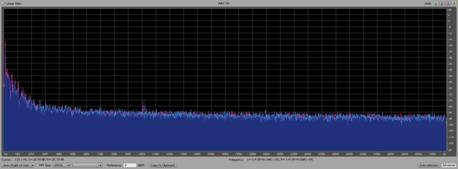
Полученные программно значения частот приведены в таблице 1:
Таблица 1
|
R, o |
Бас барабан, Гц |
Малый том, Гц |
Средний том, Гц |
Напольный том, Гц |
Рабочий барабан, Гц |
|
0 |
80 |
60 |
61 |
42 |
101 |
|
90 |
– |
84 |
85 |
63 |
144 |
|
180 |
60 |
112 |
115 |
78 |
157 |
|
270 |
– |
129 |
138 |
88 |
183 |
|
360 |
70 |
149 |
153 |
97 |
– |
|
450 |
– |
– |
– |
104 |
– |
|
540 |
80 |
– |
– |
– |
– |
Сигнал рассматривается и анализируется в программе MathCad 14. В данной программе используются функции:
READWAV (file) — чтение звукового файла в матрицу.
funcObj(F, tStart, nums, hag) — функция возвращающая массив времени и точек сигнала в эти моменты времени. В качестве параметров передаются массив точек сигнала, номер точки сигнала, с которой следует начать, номер точки сигнала на которой следует закончить и единица времени.
Cspline(vx, vy) — вычисляет массив вторых производных vs для сплайна, используемого для интерполяции данных из vx и vy.
Interp(vs, vx, vy, x) — возвращает интерполируемое значение y, соответствующее аргументу x. Вектор vs вычисляется на основе векторов данных vx и vy.
FuncToFFT(q, Lm, Fnc) — функция возвращающая массив частот и соответствующие им дискретные значения БПФ. В качестве параметров передаются степень двойки, для вычисления количества точек, множитель — интервал частот, интерполирующая функция основного сигнала.
FindMaxFreq(InMs, Lm) — функция возвращающая определённую частоту, соответствующую максимуму спектральной плотности. В качестве параметров передаётся массив точек ДПФ по времени и множитель — интервал частот.
Математическое описание характеристик и дискретных преобразований Фурье
Описание малого (рабочего) барабана при 0 градусов угла поворота крепёжных винтов:
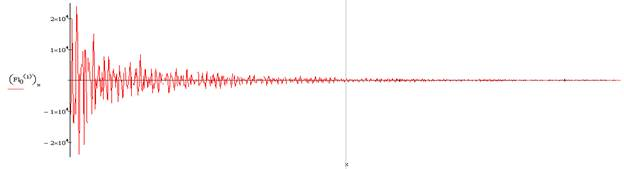
Количество точек в сигнале 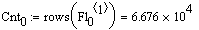
Массив точек, составленный по времени и сигналу 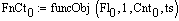
Коэффициенты интерполяции сплайнами 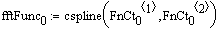
Интерполяционная функция 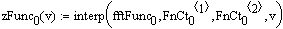
Коэффициент произведения 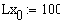
Массив результата БПФ 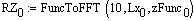
Частота колебаний при 0 градусов 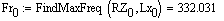 Гц
Гц
Описание малого (рабочего) барабана при 90 градусов угла поворота крепёжных винтов:
Количество точек в сигнале 
Массив точек, составленный по времени и сигналу 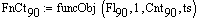
Коэффициенты интерполяции сплайнами 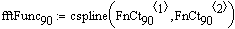
Интерполяционная функция 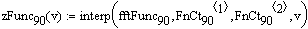
Коэффициент произведения 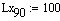
Массив результата БПФ 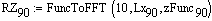
Частота колебаний при 90 градусов  Гц
Гц
Описание малого (рабочего) барабана при 180 градусов угла поворота крепёжных винтов:
Количество точек в сигнале 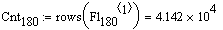
Массив точек, составленный по времени и сигналу 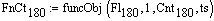
Коэффициенты интерполяции сплайнами 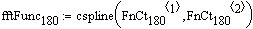
Интерполяционная функция 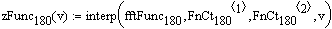
Коэффициент произведения 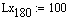
Массив результата БПФ 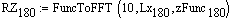
Частота колебаний при 180 градусов 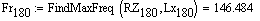 Гц
Гц
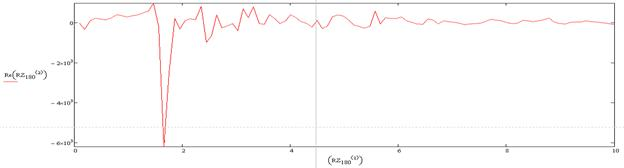
Описание малого (рабочего) барабана при 270 градусов угла поворота крепёжных винтов:
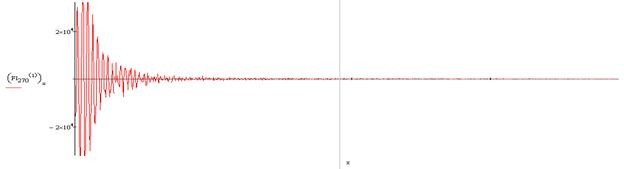
Количество точек в сигнале 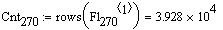
Массив точек, составленный по времени и сигналу 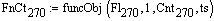
Коэффициенты интерполяции сплайнами 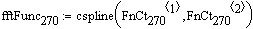
Интерполяционная функция 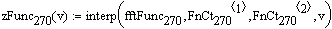
Коэффициент произведения 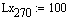
Массив результата БПФ 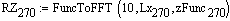
Частота колебаний при 270 градусов 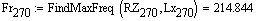 Гц
Гц
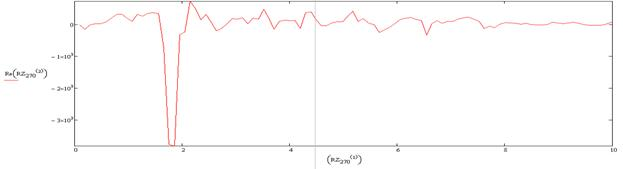
Анализ полученных результатов:
Массив углов замера Массив результирующих частот
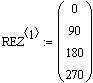
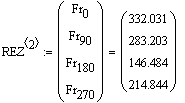
Массив сплайновых коэффициентов 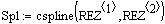
Интерполяционная функция 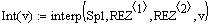
 ,
, 
Аналогичные математические описания проводились для бас барабана, малого среднего и напольного тома.
Сравнение полученных результатов
1) Программно полученный результат:
|
R, o |
Бас барабан, Гц |
Малый том, Гц |
Средний том, Гц |
Напольный том, Гц |
Рабочий барабан, Гц |
|
0 |
80 |
60 |
61 |
42 |
101 |
|
90 |
– |
84 |
85 |
63 |
144 |
|
180 |
60 |
112 |
115 |
78 |
157 |
|
270 |
– |
129 |
138 |
88 |
183 |
|
360 |
70 |
149 |
153 |
97 |
– |
|
450 |
– |
– |
– |
104 |
– |
|
540 |
80 |
– |
– |
– |
– |
2) Математически полученный результат:
|
R, o |
Бас барабан, Гц |
Малый том, Гц |
Средний том, Гц |
Напольный том, Гц |
Рабочий барабан, Гц |
|
0 |
87 |
97 |
87 |
253 |
332 |
|
90 |
– |
136 |
97 |
78 |
283 |
|
180 |
107 |
68 |
126 |
107 |
146 |
|
270 |
– |
97 |
146 |
107 |
214 |
|
360 |
87 |
97 |
166 |
117 |
– |
|
450 |
– |
– |
– |
117 |
– |
|
540 |
97 |
– |
– |
– |
– |
Разность измерений по каждому из барабанов можно отразить на графике погрешностей расчета:
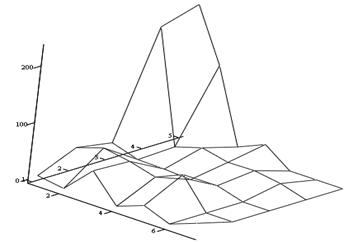
В результате получены и изучены данные, которые, могут найти применение в разработке приложений и инструкций для музыкантов в определённой сфере. Получены основные погрешности измерений, что в дальнейшем поможет найти источники несоответствий в измерениях подобного рода и получена интерполяционная функция, описывающая в определённых диапазонах поведение объекта в зависимости от частоты, что можно считать упрощённой моделью данного объекта.
Литература:
1. Купинский К. М. Школа игры на ударных инструментах / К. М. Купинский. — М.: Московская Типография № 6, 1981. — 206 с.
2. Радзишевский, А. Ю. Основы аналогового и цифрового звука / А. Ю. Радзишевский. — М.: Вильямс, 2006. — 288 с.
3. Тихонов А. Г. Статистический анализ и синтез радиотехнических устройств и систем / В. И. Тихонов, В. Н. Харисов — М.: Радио и связь, 2004. — 608 с.

