Известно, что использование моделирования позволяет организовать учебную деятельность на более сознательном продуктивном уровне. Моделирование в обучении имеет три аспекта:
- цель обучения,
- содержание процесса обучения, способ познания,
- учебное действие, являющееся составной частью деятельности (средство обучения).
В учебной практике применяется следующая схема моделирования реальной ситуации:
1) формализация — перевод условия задачи на математический язык;
2) решение проблемы как математической задачи;
3) интерпретация — перевод математического решения обратно на язык, на котором была сформулирована исходная проблема.
Эта схема описывает процесс: объект 
модель объект или: модель объектмодель. В реальности процесс моделирования более сложен.
По нашему мнению, особое внимание следует уделить последнему этапу — интерпретации, так как он связан с формированием умений анализировать, сравнивать и обобщать новые знания.
Моделирование позволяет привлекать к курсу математики смежные дисциплины, тем самым, показывая их взаимосвязь, и являясь мотивацией их изучения. При решении задач посредством моделирования студенты учатся переводу жизненных проблемных ситуаций в абстрактные модели и наоборот.
Рассмотрим применение математических моделей в матричной алгебре. Чем и покажем значение математического моделирования в мотивации изучения смежных дисциплин.
Математической моделью многих экономических задач являются матрицы. Информация, записанная в матричной форме компактна, наглядна, легко обрабатываема. Студенты свободно оперируют данными, записанными в таблицах, поэтому удобно вводить понятие матрицы на конкретном примере, показывая соответствие между таблицей и матрицей.
Допустим, обувная фабрика выпускает продукцию трех видов (сапоги, туфли и кроссовки) и поставляет её ежемесячно в течение зимы в город А в количестве 150, 50, 50 пар для каждого вида соответственно и в город В в количестве 200, 70 и 60 пар. Исходные данные удобно записывать в таблицу.
|
Город |
Поставка обуви (количество пар) |
||
|
сапоги |
туфли |
кроссовки |
|
|
А |
150 |
50 |
50 |
|
В |
200 |
70 |
60 |
Если необходимо найти количество туфель, поставленных в город А, достаточно взять число в клетке таблицы на пересечении первой строки и второго столбца, что составляет 50 пар. Если убрать в таблице названия строк и столбцов, а оставшуюся часть записать в виде 
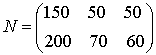, то получим пример матрицы.
Запись матрицы в общем виде (1) не вызывает трудностей, следует только обратить внимание на то, что любой элемент матрицы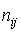 
находится на пересеченииi-й строки и j-го столбца.
, 
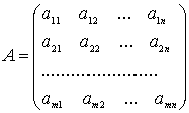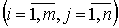(1)
Операции над матрицами также удобно изучать на примерах.
Пусть требуется определить поставки обуви за зимний период. Например, возьмем поставки сапог в город А. Ясно, что поставки будут в 3 раза больше, чем за один месяц, то есть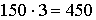 
, аналогично и для других элементов, что означает
.
Но поставки различных видов обуви в течение года различны. Пусть Z — матрица зимних поставок за один месяц, V — матрица поставок весной за один месяц.
, 
.
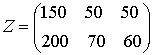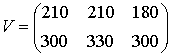Пусть необходимо найти общий объем поставок за весенне-зимний период. Очевидно, что за зиму поставлено в город А 450 пар сапог и за весну 630 пар. За весь период город А получит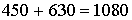 
пар сапог. Аналогично для остальных элементов.
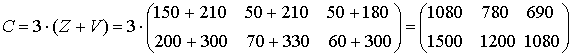
Таким образом, на этапе интерпретации получаем запись операции умножения матрицы на число (2) и сложение (вычитание) матриц (3) в общем виде:
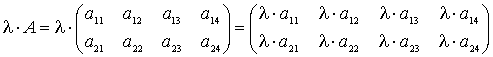, (2)
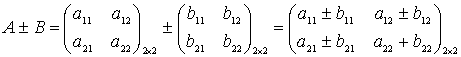. (3)
Следует обратить внимание на то, что операция сложения (вычитания) матриц вводится только для матриц одинаковой размерности.
Определенную трудность вызывает операция умножения, но и её легко разобрать на примере. Предположим, необходимо найти прибыль фабрики от поставок. Полученная матрица С показывает объем поставок всех трех видов обуви за весенне-зимний период в города А и В. Пусть фабрика получает за пару обуви каждого вида 30,15,10 у.е. соответственно. Тогда вектор-столбец прибыли можно записать в виде: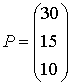 
.
Очевидно, что прибыль от продажи продукции в город А составит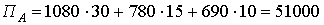 
у.е. Таким образом, перемножаются элементы, стоящие на первом, втором, третьем местах и затем результаты складываются.
.
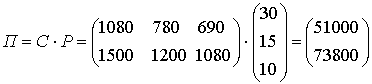Или в общем виде:
.
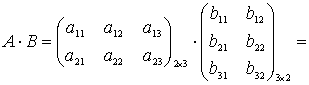
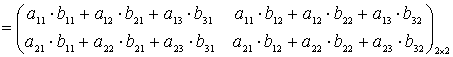Внимание студентов необходимо обратить на то, что произведение АВ существует только когда первый множитель А имеет число столбцов, равное числу строк второго множителя В. Из существования произведения АВ не следует существование произведения ВА. В случае его существования, как правило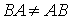 
.
Матричная алгебра применима и к решению систем линейных уравнений. На фабрике для изготовления обуви используется три вида сырья: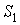 
, 
, 
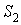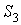. Нормы расхода сырья 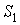на одну пару каждого вида обуви 4, 3, 4 у.е. соответственно, сырья 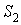— 2, 1, 1 у.е. и сырья 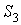— 1, 2, 3 у.е. При этом за день расходуется 2500 у.е. сырья 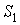, 900 у.е. — 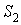и 1400 у.е — 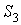. Требуется найти ежедневный объем выпуска каждого вида обуви. Предположим, что фабрика выпускает 
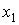пар сапог, 
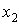— туфлей и 
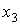— кроссовок. Тогда легко можно составить систему:
.
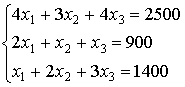Введем матрицу норм расходов сырья — А, матрицу выпуска — Х и матрицу запасов ресурсов — В, тогда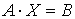 
, где
, 
, 
.
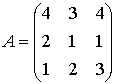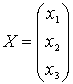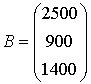Перемножая матрицы А и Х, а затем приравнивая соответствующие элементы правой и левой частей уравнения, получим систему, записанную выше. В матричном виде система линейных уравнений записывается кратко и образно, только не следует путать эту запись с обычным уравнением первой степени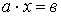 
. Решение матричного уравнения имеет вид: 
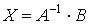. Найдем обратную матрицу 
:
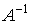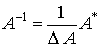, где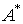 
— присоединенная матрица.
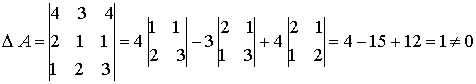
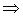матрица А невырожденная и обратная матрица существует. Найдем присоединенную матрицу 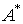, для этого запишем транспонированную матрицу А и каждый её элемент заменим алгебраическим дополнением.
.
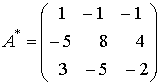Обратная матрица равна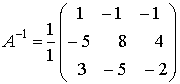 
.
Решая данное матричное уравнение, получаем
.
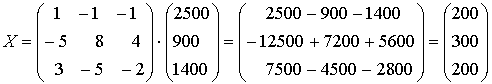Это значит, что фабрика в день выпускает 200 пар сапог, 300 пар туфлей и 200 пар кроссовок.
Таким образом, элементы матричной алгебры могут быть удачно введены с помощью экономических задач. При этом математическая теория увязывается с экономическими знаниями, что в дальнейшем дает возможность решать более сложные экономические задачи. Применение моделирования способствует решению нескольких методических задач:
- усилению мотивационной составляющей обучения математики, смежных экономических дисциплин;
- развитию умственных способностей студентов, необходимых им в дальнейшей профессиональной деятельности.
Литература:
1. Возняк Г. М. Прикладные задачи в мотивации обучения // Математика в школе № 2, 1990, С.9–11.
2. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера — М.: ЮНИТИ, 2003, 471 с.
3. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах // Молодой ученый № 12 (59), 2013, С.3–6.
4. Куимова Е. И., Куимова К. А., Ячинова С. Н. Формирование мотивационной составляющей обучения на примере изучения дифференциальных уравнений // Молодой ученый № 2 (61), 2014, С.775–777.
5. Родионов М. А. Мотивация учения математике и пути её формирования: Монография. — Саранск: Издательство МГПИ им. М. Е. Евсевьева, 2001, 252 с.
