Введение
В геотехническом строительстве взаимодействие грунтовых массивов с конструктивными элементами имеет ключевое значение при оценке устойчивости сооружений. Под действием природных и техногенных нагрузок давление грунта вызывает изгиб и деформации пластин, а также формирование напряжённого состояния в конструкциях. Подобные явления наблюдаются в подпорных стенах, панелях откосов, фундаментных плитах и лабораторных моделях. Анализ деформаций позволяет получить достоверную информацию о совместной работе системы «грунт–сооружение» [1,4,5]. Классические методы определения давления грунта, основанные на теориях Кулона [2] и Ранкина [3], широко применяются в инженерной практике, однако во многих случаях они упрощённо отражают реальное распределение напряжений. В механике конструкций прогиб пластин определяется на основе дифференциальных уравнений с учётом граничных условий и характера нагрузок, после чего по функции прогиба оцениваются напряжения. Вместе с тем такие подходы не всегда учитывают нелинейные свойства грунта. Современные исследования показывают, что применение экспоненциальных зависимостей для описания прогиба пластин позволяет повысить точность оценки напряжённого состояния грунта при действии собственного веса и дополнительной нагрузки [13, 14]. В связи с этим анализ прогиба пластин и восстановление по нему распределения напряжений является актуальным и перспективным направлением исследований.
Цель и задачи исследования. Целью настоящей работы является теоретическое и экспериментальное исследование прогиба пластины под действием собственного веса грунта и дополнительной пригрузки, а также определение напряжений на основе функции прогиба с сопоставлением полученных результатов с классическими моделями механики грунтов. Для достижения поставленной цели в работе выполнены расчёт деформаций пластины на основе классического уравнения изгиба, разработка аналитической экспоненциальной зависимости, определение напряжённого состояния путём дифференцирования функции прогиба и сравнение результатов с традиционной зависимостью «давление–глубина». Оценена теоретическая и практическая значимость предложенного подхода и обоснована его применимость при решении современных геотехнических задач, включая расчёт устойчивости откосов, подпорных стен и пластинчатых конструкций.
Экспериментальные исследования и анализ результатов. Для оценки устойчивости откосов проведены модельные испытания в лабораторном плоском грунтовом лотке со стальной пластиной, жёстко защемлённой в основании и свободной в верхней части. Такая схема моделирует работу подпорной стенки, воспринимающей давление грунта со стороны откоса. В ходе испытаний тыльная сторона пластины послойно заполнялась мелким песком и щебнем. Давление грунта формировалось за счёт его удельного веса γ и дополнительной поверхностной пригрузки q 0 под действием которых верхняя часть пластины испытывала горизонтальный прогиб.В экспериментах использовалась стальная пластина высотой 1,25 м, шириной 0,26 м и толщиной 5 мм. Модуль упругости стали составлял 2,1×10 5 МПа, момент инерции сечения определялся расчётным путём. Прогиб пластины измерялся линейными датчиками перемещений (LVDT) с разрешением 0,01 мм; все приборы предварительно калибровались, а измерения выполнялись не менее трёх раз. Оценка прогиба осуществлялась экспериментальным методом на основе прямых измерений горизонтальных перемещений пластины.
С учётом жёсткого защемления в нижней части пластина рассматривалась как консольная балка. Для консольной балки, нагруженной линейно изменяющейся (треугольной) распределённой нагрузкой, профиль прогиба определялся с использованием классического аналитического решения, полученного в рамках сопротивления материалов для треугольного распределения нагрузки на консоль.
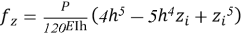
Здесь P обозначает линейно изменяющуюся (треугольную) распределённую нагрузку, действующую на консоль вследствие собственного веса грунта (кПа); EI — изгибную жёсткость консоли (кН·м²); h — высоту консольного элемента (м); zᵢ — отметку (или глубину) рассматриваемой точки вдоль консоли (м).
При действии на грунт дополнительной поверхностной пригрузки прогиб пластины определялся с учётом трапецеидально распределённой нагрузки и рассчитывался соответствующим образом.
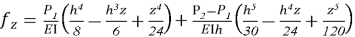
Здесь P₁ обозначает давление пригрузки, приложенной к поверхности грунта (кПа), а P₂ — суммарное давление, обусловленное действием собственного веса грунта и дополнительной пригрузки (кПа).
Приведённые уравнения используются для определения линейно изменяющихся нагрузок, обусловленных собственным весом грунта и дополнительной пригрузкой. На их основе выполнены численные расчёты и получена функция прогиба, сопоставление которой с экспериментальными данными представлено на рисунке 1.

Рис. 1. Сопоставление расчётных и экспериментальных прогибов пластины: (a) щебень; (b) песок. 1 – аналитический (линейный) прогиб; 2 – экспериментальный прогиб
Из графика видно, что экспериментально полученный прогиб пластины существенно меньше теоретически рассчитанного прогиба консольного листа. С учётом данного обстоятельства дифференциальное уравнение изгиба вдоль нейтральной оси консоли записывается в следующем виде:
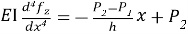
Отсюда распределённые давления определяются как
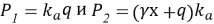
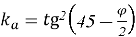
φ — угол внутреннего трения грунта (в градусах). Краткое замечание о общем решении,
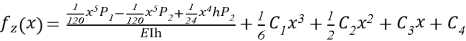
Интеграционные постоянные в данном уравнении определяются из граничных условий для консольной балки с жёстким защемлением в одном конце и вычисляются при x=0 и x=h соответственно.
f
z
(0)=0;
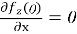

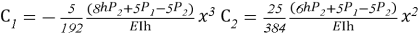
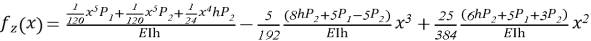
С использованием уравнения (5) была построена функция прогиба консольной балки. Для сопоставления прогиба, полученного по уравнению (5), с результатами, вычисленными по уравнениям (1) и (2), обе зависимости представлены на рисунке 2.
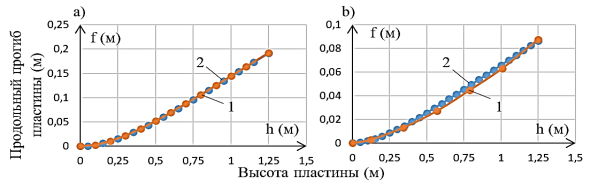
Рис. 2. График продольного прогиба пластины: (а) прогиб пластины, определённый дифференциальным и традиционным методами и (b) продольный прогиб, определённый по экспоненциальной модели и по экспериментальным данным. 1 — экспериментальный продольный прогиб пластины; 2 — продольный прогиб, полученный по экспоненциальному уравнению
Данное уравнение описывает прогиб консольной балки (подпорной стенки) при действии линейно изменяющихся нагрузок. С использованием уравнения (5) получена функция прогиба, которая, как видно из рисунка 2,а, совпадает с теоретически рассчитанным результатом. В связи с этим далее рассматривается решение задачи прогиба консольной балки при экспоненциально изменяющейся нагрузке, при этом криволинейное распределение нагрузки принимается в экспоненциальной форме с условием равенства её площади площади соответствующей трапецеидальной нагрузки.
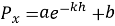
Для граничных условий при
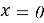
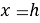
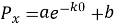
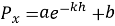
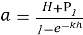
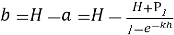
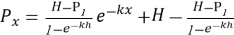
Из данного выражения выполняется интегрирование функции Px, после чего полученный результат приравнивается площади трапецеидальной нагрузки.
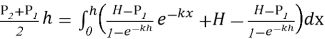
Из интегрального решения (6) определяется неизвестный параметр H. В данном уравнении величина H характеризует значение давления при x=h.
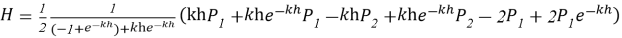
Формулируем дифференциальное уравнение изгиба вдоль нейтральной оси балки:
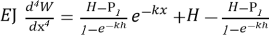
Получаем общее решение:
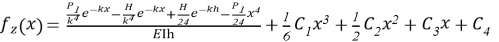
Интеграционные постоянные в данном уравнении определяются соответственно при
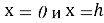
f
z
(0)=0;
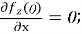
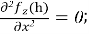
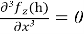
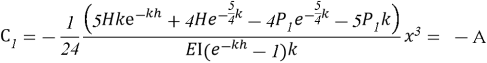
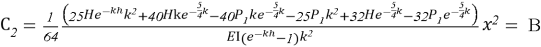
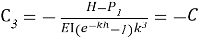
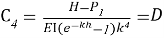
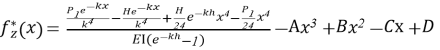
С использованием указанного дифференциального уравнения на рисунке 2б построена кривая прогиба балки с изгибной жёсткостью EI при равномерно распределённых нагрузках, соответствующих трапецеидальному и экспоненциальному профилям.
На основе ранее полученного выражения (10) были определены значения напряжений в грунте на заданных высотах пластины и выполнено их сопоставление с результатами, полученными по традиционной теории Кулона — Мора. В механике грунтов пластина рассматривается как подпорная стенка, при этом давление от собственного веса грунта имеет треугольное распределение, а при наличии дополнительной пригрузки на откосе — трапецеидальное. Среди классических подходов к решению данной задачи наибольшее распространение получили линейные методы Ранкина [1] и Кулона [2]. Предполагая, что откос за подпорной стенкой находится в состоянии предельного равновесия, можно считать, что при равномерно распределённой нагрузке главные напряжения действуют в горизонтальной плоскости, проходящей через любую точку за стенкой.

Определим горизонтальное давление грунта, действующее на подпорную стенку:
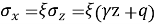
Равнодействующие силы формируют активное давление грунта по отношению к подпорной стенке.
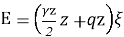
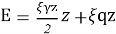
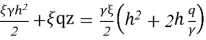
В этом случае для несвязных грунтов-таких как песок и щебень-при C=0 и φ≠0 соотношение между главными напряжениями записывается следующим образом:
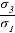
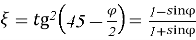
На основании уравнений (15) и (16)

Полученные данные позволяют определить линейные распределения нагрузок на подпорную стенку, обусловленные собственным весом грунта и действием дополнительной нагрузки. В соответствии с теорией линейного распределения нагрузок давление, действующее на подпорную стенку, убывает с увеличением высоты (или, соответственно, возрастает с глубиной).
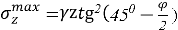
Здесь



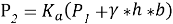
В данной формуле Р 1 - представляет собой величину дополнительной (пригрузочной) нагрузки, передаваемой на грунт; при отсутствии пригрузки принимается Р 1 =0.
С использованием четвёртой производной экспоненциального уравнения и соотношений Кулона — Мора были определены значения напряжений в грунте по высоте пластины, на основе которых построена эпюра результирующего воздействия на пластину. График указанной эпюры напряжений представлен на рисунке 3.
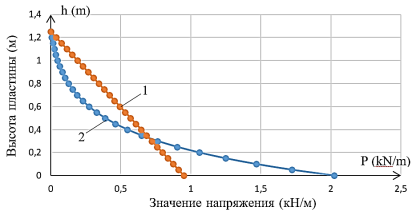
Рис. 3. Сравнение эпюр напряжений грунта: 1 – по теории Кулона — Мора (линейная); 2 – по экспоненциальной модели (параболическая)
На рисунке 3 показано, что эпюра напряжений, рассчитанная по теории Кулона — Мора, имеет линейный характер, тогда как эпюра, полученная на основе четвёртой производной экспоненциальной зависимости, является криволинейной (параболической). Это приводит к уменьшению изгибающего момента при параболическом распределении давления по сравнению с традиционным расчётом, поскольку равнодействующая активного давления Ea располагается ближе к основанию стенки, а не на высоте h/3. Указанное обстоятельство свидетельствует о том, что экспоненциальная модель более адекватно отражает реальное напряжённое состояние при оценке устойчивости откосов и подпорных стен.
Обсуждение. Предложенная экспоненциальная модель верифицирована в условиях статического нагружения и лабораторных исследований в малом масштабе и показала хорошее согласование с экспериментальными данными. Вместе с тем модель не учитывает времязависимое и динамическое поведение грунта. В дальнейшем целесообразно расширить данный подход на условия динамического и сейсмического воздействия с применением численного моделирования в программных комплексах PLAXIS 3D, ABAQUS и MIDAS GTS, а также выполнить крупномасштабные натурные испытания для оценки практической применимости модели.
Заключение.
Проведённые исследования показали, что прогиб и напряжённое состояние пластины под действием собственного веса грунта и дополнительной пригрузки более точно описываются экспоненциальной моделью по сравнению с традиционными подходами. Сопоставление экспериментальных и теоретических результатов свидетельствует о том, что напряжения, определённые на основе экспоненциальной зависимости, лучше соответствуют реальному поведению системы, чем линейное распределение по теории Кулона — Мора. Полученные результаты подтверждают возможность применения экспоненциальной модели при оценке устойчивости откосов и подпорных стен, а также при анализе напряжённо-деформированного состояния системы «сооружение–грунт». Предложенный подход может повысить точность расчётов и экономическую эффективность инженерных решений.
Вместе с тем исследование выполнено для условий статического нагружения. В дальнейшем целесообразно рассмотреть применение экспоненциальной модели при динамических и сейсмических воздействиях, а также для различных типов грунтов с использованием численного моделирования и натурных испытаний.
Литература:
- Xasanov A. Z. Xasanov Z. A. Stability of Natural Slopes and Determination of the Pressure of Incoherent Soils on Fences” Springer, 2024.
- Coulomb, C. A. (1776). Essai sur une application des règles de maximis et minimis à quelques problèmes de statique relatifs à l’architecture. Paris.
- Rankine, W. J. M. (1857). On the stability of loose earth. Philosophical Transactions of the Royal Society of London, 147, 9–27. https://doi.org/10.1098/rstl.1857.0003
- Terzaghi, K. (1943). Theoretical Soil Mechanics. John Wiley & Sons.
- Bowles, J. E. (1996). Foundation Analysis and Design (5th ed.). McGraw-Hill.
- Craig, R. F. (2012). Craig’s Soil Mechanics (8th ed.). CRC Press. https://doi.org/10.1201/b12804
- Timoshenko, S., & Woinowsky-Krieger, S. (1959). Theory of Plates and Shells. McGraw-Hill.
- Choudhury, D., & Nimbalkar, S. (2006). Seismic passive earth pressure coefficients using pseudodynamic method. Journal of Geotechnical and Geoenvironmental Engineering, 132(12), 1541–1548. https://doi.org/10.1061/(ASCE)1090–0241(2006)132:12(1541)
- Chen, G., Xu, B., & Sun, H. (2019). Numerical analysis of retaining wall under combined static and dynamic loading. Computers and Geotechnics, 112, 220–231. https://doi.org/10.1016/j.compgeo.2019.04.018
- Li, X., & Wang, Y. (2020). Analytical solutions for deflection of retaining walls subjected to soil pressure. Soil Mechanics and Foundation Engineering, 57(2), 123–130. https://doi.org/10.1007/s11204–020–09531–1
- Xu, L., & Zhou, Y. (2023). Exponential distribution models for soil pressure on retaining walls. International Journal of Geomechanics, 23(4), 04023045. https://doi.org/10.1061/(ASCE)GM.1943–5622.0002621
- Bhattacharya, S., & Bolton, M. D. (2021). Experimental study on soil–structure interaction of retaining elements under lateral loads. Géotechnique, 71(3), 210–225. https://doi.org/10.1680/jgeot.19.P.293
- Kramer, S. L. (2014). Geotechnical Earthquake Engineering. Pearson Education.
- Zienkiewicz, O. C., Pastor, M., & Chan, A. H. C. (2020). Computational Geomechanics with Special Reference to Earthquake Engineering. CRC Press. https://doi.org/10.1201/9780429343441
- Khosravi, A., & Taiebat, H. (2022). Advanced constitutive models for seismic slope stability assessment. Soil Dynamics and Earthquake Engineering, 156, 107230. https://doi.org/10.1016/j.soildyn.2022.107230
- Zhang, J., & Ling, H. I. (2021). Stress–strain response of granular soils under combined loading conditions. Journal of Geotechnical and Geoenvironmental Engineering, 147(7), 04021056. https://doi.org/10.1061/(ASCE)GT.1943–5606.0002517
- Hassan, A. M., & El Naggar, H. (2020). Numerical modeling of soil–structure interaction in retaining systems. Soil Mechanics and Foundation Engineering, 57(6), 421–430. https://doi.org/10.1007/s11204–020–09549–5
- Wang, G., & Gao, L. (2021). Application of nonlinear soil models in slope stability analysis. Engineering Geology, 288, 106145. https://doi.org/10.1016/j.enggeo.2021.106145
- Zhou, H., & Li, N. (2022). Analytical method for lateral earth pressure on retaining walls considering soil arching effect. International Journal of Geomechanics, 22(10), 04022156. https://doi.org/10.1061/(ASCE)GM.1943–5622.0002345
- Bhattacharya, S., Bolton, M. D., & Madabhushi, S. P. G. (2020). Seismic behaviour of retaining walls: Experimental and numerical insights. Géotechnique Letters, 10(2), 205–213. https://doi.org/10.1680/jgele.20.00044
- International Organization for Standardization. (2019). ISO 23469:2019—Bases for design of structures: Seismic actions for geotechnical design. ISO.
- Ministry of Construction of the Republic of Uzbekistan. (2020). KMK 2.01.03–19: Construction considering seismic actions. Tashkent: Ministry of Construction. [In Uzbek]

