Обработка результатов экспериментальных исследований влияния деформационной анизотропии на величину модуля сдвига грунтовых образцов



Главной проблемой современного строительства является надежное прогнозирование напряженно-деформированного состояния, поэтому необходимо учитывать реальные свойства грунтовых оснований, что позволит получить наиболее надежные и экономичные варианты фундаментов при обеспечении достаточной безопасности в процессе их эксплуатации. Экспериментальные исследования влияния деформационной анизотропии грунтов на величину сопротивления сдвигу образцов, отобранных с различных глубин по взаимно перпендикулярным направлениям, были выполнены в приборе одноплоскостного среза. Кроме этого, были поставлены задачи выявить влияние деформационной анизотропии на модуль сдвига G и на угол наибольшего отклонения max. Лабораторные испытания для определения величины сопротивления сдвигу проводились методом одноплоскостного среза согласно ГОСТ 12248–2012 «Грунты. Методы лабораторного определения характеристик прочности и деформируемости» прибором ПСГ-2М.

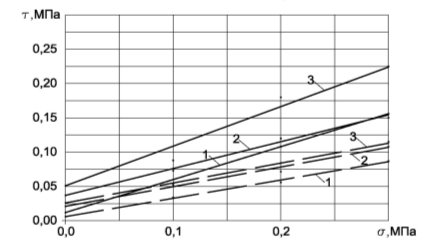
Рис. 1. Зависимость сопротивления сдвигу τ, МПа от давления σ, МПа на глубине 2,0 м: 1 — супесь твердая; 2 — суглинок тугопластичный; 3 — глина полутвердая;

Испытанные образцы в вертикальном направлении

Испытанные образцы в горизонтальном направлении

Испытывались образцы разных видов грунта (супеси, суглинки и глины), отобранные на глубинах 2,0; 4,0; 6,0; 9,0 м. По результатам, полученным лабораторными испытаниями образцов, были построены графики зависимости сопротивления сдвигу τ, МПа от давления σ, МПа на разных глубинах. В качестве примера на рисунке 1 представлены результаты образцов трех видов грунта, отобранных на глубине 2,0 м в двух взаимно перпендикулярных направлениях. Анализ результатов показал, что величина сопротивления сдвигу постепенно возрастает до определенной глубины, но затем начинает снижаться. Это связано с тем, что с увеличением глубины деформации в грунтовых основаниях начинают затухать.

Чтобы выявить влияние деформационной анизотропии грунтов на величину модуля сдвига были исследованы образцы, отобранные вдавливанием колец в грунт, как в вертикальном, так и в горизонтальном направлениях. Модули сдвига G были определены по зависимости:

G = /, (1)

где  — сопротивление сдвигу;  — деформация сдвига

При обработке данных были получены зависимости изменения величины модуля сдвига от величины сдвиговых деформаций, из чего можно сделать вывод, что величина модуля сдвига образца, отобранного в вертикальном направлении, превышает по значению образец, отобранный в горизонтальном направлении. Лабораторные испытания для определения модуля деформации проводились согласно ГОСТ 12248–2012 «Грунты. Методы лабораторного определения характеристик прочности и деформируемости» автоматическим компрессионным релаксометром АКР-2.

Испытывались образцы разных видов грунта (супеси, суглинки и глины), отобранные на глубинах 2,0; 4,0; 6,0; 9,0 м. По результатам, полученным в лабораторных испытаниях, составлена (таблица 1) результатов расчета коэффициента анизотропии грунтов, α. Для каждого вида грунта было рассчитано среднее значение коэффициента анизотропии α. Наряду с вышеперечисленными исследованиями была рассмотрена область пластических деформаций — потенциальная зона разрушения грунта.

Влияние показателя деформационной анизотропии α на угол наибольшего отклонения max. Исследование, позволяющее оценить степень приближения напряженного состояния основания к предельному.

Таблица 1

Результаты расчета коэффициента анизотропии грунтов, α

Наименование грунтов	Глубина отбора пробы, м	Значения модуля деформации по данным компрессионных испытаний, МПа		Коэффициент анизотропии, α
		образцов, вырезанных перпендикулярно (вертикально) плоскости изотропии, Еверт.	образцов вырезанных параллельно (горизонтально) плоскости изотропии, Егор.	частные значения	средние значения
Супесь твердая	2,0	10,1	10,3	0,98	1,06
	4,0	12,5	11,6	1,08
	6,0	11,1	10,3	1,08
	9,0	13,5	12,0	1,12
Суглинок тугопластичный	2,0	6,3	5,3	1,21	1,17
	4,0	4,3	3,7	1,16
	6,0	16,9	14,2	1,19
	9,0	16,0	14,6	1,10
Глина полутвердая	2,0	6,5	5,4	1,20	1,23
	4,0	5,9	4,8	1,22
	6,0	8,3	6,6	1,25
	9,0	9,2	7,4	1,24

Для этого в каждой характерной зоне вычислялись величины главных напряжений: определялся max — угол наибольшего отклонения полного давления от нормали к площадке, на которой оно действует:

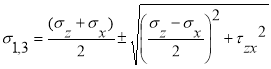, (2)

sinmax = (1 — 3)/(1+3 +2с*сtg ), (3)

Напряжения σ1 и σ3 вычислены по известным зависимостям теории напряжений при осредненных (для каждой из зон I-III) значениях напряжений σz, σx и τzx.

В случае несвязного грунта удельное сцепление в грунте с = 0. Зависимость отношения θmaxα / θmax от показателя анизотропии α при ρ = 0,1 и 0,5 МПа. Как было установлено, практически неизменным при изменении α ( = Еz/Ex, где Еz и Ex — модули деформации в вертикальном и горизонтальном направлениях) значениям σz (в зонах I... III) соответствуют увеличивающиеся (при α < 1) или уменьшающиеся (при α > 1), по сравнению с решением изотропной среды, значения σx и τzx. Это обстоятельство усиливает или снижает тенденцию к появлению сдвигов в этих зонах. Так, расчетом установлено, что при значениях α = 1; 2 и 0,5 (νzx = νyx = 0,30) среднее для зоны I значение угла наибольшего отклонения θmax = 63º, 79º и 48º соответственно. Это означает, что при прочих равных условиях, показателю α = 2 будет соответствовать уменьшенное значение расчетного сопротивления грунта основания R, а показателю α = 0,5 — увеличенное, по сравнению с расчетным сопротивлением, установленным для изотропной полуплоскости.

Таблица 2

Пример вычисления угла наибольшего отклонения (для зоны 1;  = 0,3)

Ez = Ex  = 1	Ez > Ex  = 2	Ez < Ex  = 0.5
z = 0,161 МПа x = 0,037 МПа zx = 0,063 МПа	z = 0,161 МПа x = 0,017 МПа zx = 0,050 МПа	z = 0,161 МПа x = 0, 078 МПа zx = 0,080 МПа
А.(z+x)/2= 0,099 (z-x)/2= 0,062 ((z-x)/2)2.= 0,003844 2zx = 0,003969	0,0890 0,0720 0,005184 0,00250	0,1195 0,0415 0,001521 0,0064
Б. = = 0,08839	0,087658	0,089
1 =А+Б = 0,18739 3 = А-Б = 0,01061	1 = 0,17666 3 = 0,001342	1 = 0,2085 3 = 0,0305
(1 -3)/(1+3)= 0,17678/0,1980=0,8928 sin max = 0,8928 max = 63,13	0,175318/0,178002 0,985 sin max = 0,985 max = 79	0,178/0,239 0,745 sin max = 0,745 max = 48,12
эталон — расчетное сопротивление — R, при p = const — b	основание слабее, чем при =1,R1 < R, при b =const –b1 > b	основание прочнее, чем при =1,R2 >R, при р=const –b2 < b
В пределе: сила предельного сопротивления основания Fu [1]	Если  — одноосное сжатие Fu1< Fu	Если  — компрессия Fu2 > Fu

В зоне II значениям α = 1; 2 и 0,5 соответствуют величины θmax =30º, 41º и 11º; в зоне III — θmax = 52º, 60º и 39º. Как видно, в каждой из зон влияние изменения α на величину θmax качественно одинаково. Однако, при любом значении α, угол θmax в зоне I больше, чем в других зонах, в зоне II — он минимален. Эти данные хорошо согласуются с экспериментальными результатами, свидетельствующими о развитии областей сдвигов в зоне I и появлении уплотненного ядра в зоне II, где напряженное состояние далеко от предельного. Примеры вычисления угла наибольшего отклонения θmax для зон I — III приведены в таблицах 2–4.

Таблица 3

Пример вычисления угла наибольшего отклонения (для зоны II;  = 0,3)

Ez = Ex  = 1	Ez > Ex  = 2	Ez < Ex  = 0,5
z = 0,310 МПа x = 0,110 МПа zx = 0,002 МПа	z = 0,310 МПа x = 0,064 МПа zx = 0,004 МПа	z = 0,310 МПа x = 0,210 МПа zx = 0,003 МПа
А.(z+x)/2= 0,21 (z-x)/2= 0,10 ((z- x)/2)2 = 0,01  2zx = 0,000004	0,187 0,123 0,01513 0,000016	0,260 0,050 0,0025 0,000009
Б. = = 0,10	0,123	0,05
1 = 0,31 3 = 0,11	1 = 0,31 3 = 0,064	1 = 0,31 3 = 0,21
(1 -3)/(1+3)=0,51 sin max = 0,5 max = 30	0,66 sin max = 0,66 max = 41,18	0,19 sin max = 0,19 max = 11
Эталон R b	слабее, R1 < R b1 > b	прочнее, R2 > R b2 < b
В пределе: Fu	одноосное сжатие Fu1 < Fu	компрессия Fu2 > Fu

Таблица 4

Пример вычисления угла наибольшего отклонения (для зоны III;  = 0,3)

Ez = Ex  = 1	Ez > Ex  = 2	Ez < Ex  = 0,5
z = 0,311 МПа x = 0,036 МПа zx = 0,003 МПа	z = 0,315 МПа x = 0,022 МПа zx = 0,001 МПа	z = 0,303 МПа x = 0,068 МПа zx = 0,010 МПа
А.(z+x) = 0,347 (z-x) = 0,275	0,337 0,293	0,371 0,235
sin max = 0,79 max = 52,12	sin max = 0,87 max = 60,5	sin max = 0,64 max = 39,4
эталон R	слабее, R1	прочнее, R2>R
в пределе — Fu	одноосное сжатие — Fu1 < Fu	компрессия — Fu2 > Fu

По всем трем зонам I — III результаты качественно одинаковы:

Эталон, R	Слабее, R1	прочнее, R2>R
Fu	Fu1	Fu2>Fu
b	b1>b	b2

Соотношение между b, b1 и b2 определяется соотношением полных (природных плюс дополнительных) главных напряжений, а не только соотношений исследованных напряжений от нагрузки, которую можно считать дополнительной (к природной). Осадки фундамента зависят не только от  = Ez / Ex, но и от величины Ez (в большей степени, чем от ). Полученные расчетом компоненты напряжений σz, σx и τzx достаточны для полной оценки напряженного состояния полуплоскости и выявления тенденции к упрочнению или разрушению анизотропной среды в каждой из рассмотренных зон I — III при изменении показателя анизотропии α.

Выводы. Учет деформационной анизотропии грунта в зонах I — III приводит к изменению размеров зон сдвигов и величины расчетного сопротивления грунта R, следствием чего является необходимость проведения корректировки размеров фундаментов по сравнению с размерами, установленными без ее учета. При возрастании показателя анизотропии α в каждой из рассмотренных зон I — III происходит нарастание признаков, соответствующих появлению условий предельного напряженного состояния, что необходимо учитывать в расчетах грунтовых оснований, что, в свою очередь, позволит повысить обоснованность, точность и надежность принимаемых решений.

Литература:

1. Свод правил СП 22.1333.2011. Основания зданий и сооружений. Актуализированная редакция СНиП 2.02.01–83*. — М.: Министерство регионального развития, 2011. — 160с.
2. ГОСТ 12248–2012 «Грунты. Методы лабораторного определения характеристик прочности и деформируемости»
3. Коробова О. А., Максименко Л. А. Методы усовершенствования расчета осадок грунтовых оснований //Интерэкспо Гео-Сибирь: Сб. материалов XI Междунар. науч. конф. (13–25 апреля 2015 г.), г. Новосибирск: СГУГиТ, 2015. — Т.1. — № 1, — С.194–199.
4. Коробова О. А., Максименко Л. А. Результаты исследования численными методами влияния мощности анизотропных линейно-деформируемых слоев на их осадки //Интерэкспо Гео-Сибирь: Сб. материалов XII Междунар. науч. конф. (18–22 апреля 2016 г.), г. Новосибирск: СГУГиТ, 2016. — Т.2. — С.125–13.
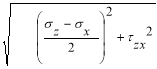
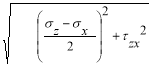