В статье впервые рассматривается применение коэффициента сложности рельефа для выбора оптимальных проектных поверхностей в инженерно-проектных задачах вертикальной планировки.
Ключевые слова: рельеф, проектная поверхность, степень сложности рельефа.
Степень сложности рельефа является важнейшим фактором в принятии решения реализации различного рода инженерных задач и в то же время наименьше изученным. Следует отметить, что степень сложности или степень расчлененности рельефа имеет словесное описание, как рельеф равнинной или холмистой местности, сильно расчлененная поверхность, спокойный рельеф и т. д. и не имеет числовых характеристик, что очевидно, представляет основную трудность использования их на практике.
В трудах [1] даётся описание определению степени сложности геометрической модели ТП, где «суммарные абсолютные внутренние и внешние кривизны вершин определяют степень сложности модели». Там же дается определение, что «простейшая поверхность — плоскость — независимо от количества рассматриваемых вершин обладает степенью сложности, равной «0». В инженерной практике методология определения степени сложности или степени расчлененности рельефа является мало изученным. В трудах [2] имеется подход к решению данной задачи методами теории вероятностей и математической статистики, основанная на данные извлекаемые из топографического плана местности. Работа основана на отношения сгущения изолиний в дм2 и учитывает признаки линий водоразделов, тальвегов боровок, подошв и т. д. Данный подход на наш взгляд является не применим к цифровым моделям рельефа (ЦМР), так как современная ЦМР основана на регулярной или нерегулярной сети данных. Следовательно, степень сложности рельефа непосредственно связана с этими данными и может быть определена взаимоотношениями этих данных.
Рассмотрим поверхность, с минимальным количеством точек, где три точки в пространстве однозначно определят плоскость [3,4,5], для которой степень сложности равна «0». Четыре точки в пространстве могут определять либо плоскость, либо косую плоскость, но не могут определить замкнутую выпуклость или вогнутость. Пересечение двух или трех плоскостей заданных на прямоугольной регулярной сети образуют усеченную, не замкнутую вершину. Следовательно, для прямоугольной регулярной сети справедливо рассмотрение четырех взаимно пересекающихся плоскостей, которые определят в частном случае, как плоскость, так и характер выпуклости или вогнутости рассматриваемой поверхности (Рис.1).
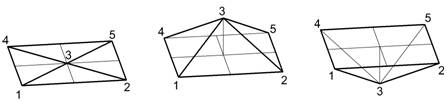
Рис. 1. Взаимное пересечение четырех плоскостей на прямоугольной сети данных
На прямоугольной регулярной сети, рассматриваемые четыре плоскости, задаются девятью узлами регулярной сети (3×3) и образуют квартал из четырех ячеек (квадрантов).
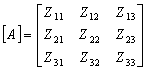 (1.1)
(1.1)
Установим некоторое взаимоотношение между девятью членами матрицы методом конечных разностей:
1. Суммируем абсолютные значения разницы элементов строк и дифференцируем:
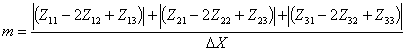 (1.2)
(1.2)
где ΔX — шаг прямоугольной регулярной сети вдоль строк.
2. Суммируем абсолютные значения разницы элементов столбцов и дифференцируем:
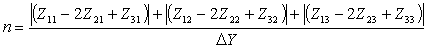 (1.3)
(1.3)
где ΔY — шаг прямоугольной регулярной сети вдоль столбцов.
3. Суммируем абсолютные значение разницы элементов диагонали и так же дифференцируем:
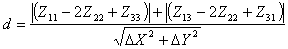 (1.4)
(1.4)
Уравнения (1.2–1.4) суммируем и получим некоторое значение — ξ для квартала поверхности:
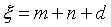 (1.5)
(1.5)
Уравнение (1.5) удовлетворяет определению степени сложности плоскости ξ=0 и выдаёт различные значения, если рассматриваемая поверхность (квартал) не плоскость.
Степень сложности нерегулярной (топографической) поверхности можно определить также, рассматривая ТП как совокупность граничащих регулярных поверхностей, и сумма степени сложности кварталов дает некоторое представление о степени сложности ТП в целом. Следовательно, степень сложности всего участка поверхности будет:
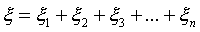 (1.6)
(1.6)
Если регулярная сеть по строкам и столбцам не делится без остатка на три, следует установит четыре системы отсчета кварталов и определить степень сложности поверхности в целом:
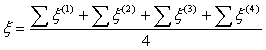 (1.7)
(1.7)
где ξ(1), ξ(2), ξ(3), ξ(4) — сложность кварталов первой, второй, третей и четвертой системы отсчета соответственно.
На основе вышеизложенных уравнений нами разработана программа «Сложность рельефа» в среде программирования Delphi. В данном приложении можно рассматривать степень сложности кварталов по каждой системе отсчета (Рис.2).
Во вкладке «Картограмма» можно наглядно рассмотреть поверхность в плановом виде с требуемым уровнем горизонталей и выявленными сложностями участков (Рис.3). При этом можно варьировать численными значениями «dh» и «Сложности от:___до___».
а) 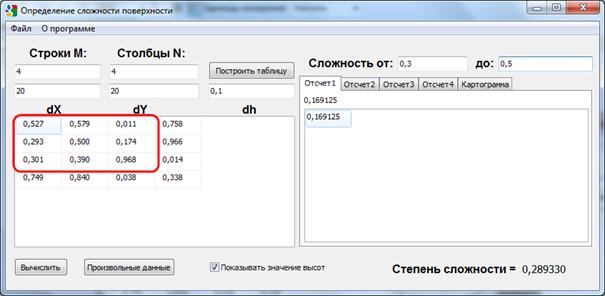
b) 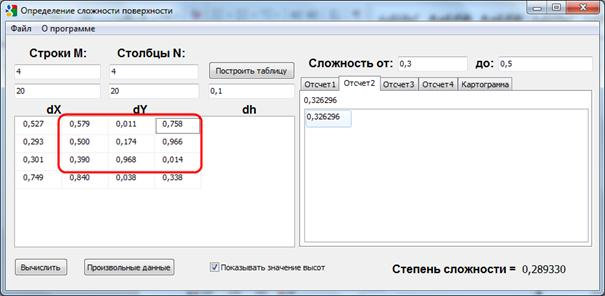
c) 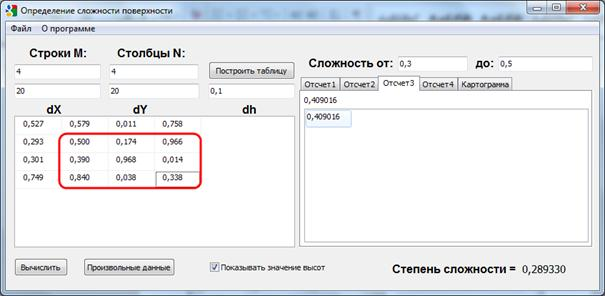
d) 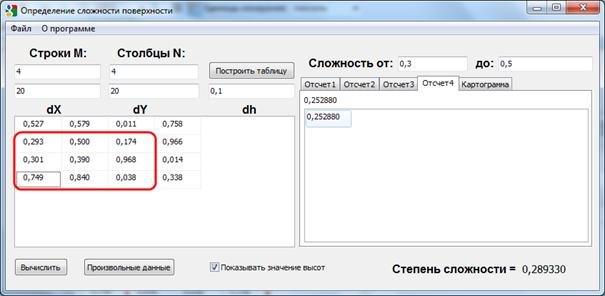
Рис. 2. Сложность рельфа по кварталам.
а) 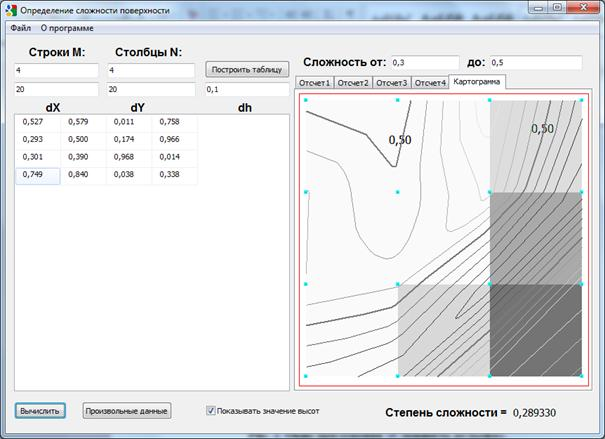
b) 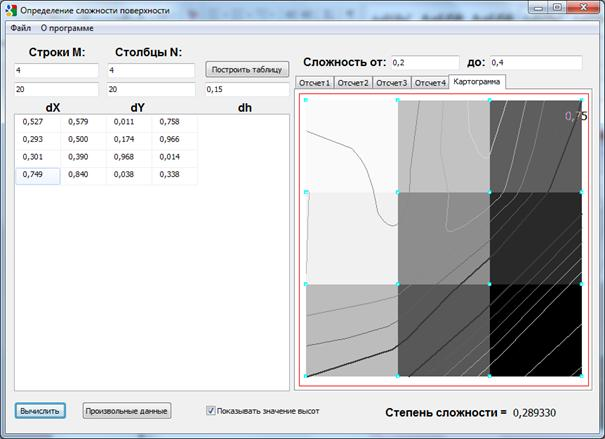
Рис. 3. Картограмма сложности рельефа.
Численные значения сложности проектной поверхности дают возможность выбора реализации проекта, решать различные инженерные задачи, связанные с проектированием проектной поверхности, возможностью подсчета энергоресурсов, ввести некоторые коэффициенты по степени сложности для реализации проекта и т. д.
Предлагаем к сотрудничеству в данной области.
Отзывы по статье направить на e-mail: xb75@mail.ru
Литература:
1. Кучкарова Д. Ф. Теория топографических поверхностей и ее приложения. Дисс. на соискание ученой степени д. т.н. Бухара, 2001. — 314 с.
2. Хейфец Б. С., Хромченко А. В. Применение теории информации для оценки степени расчлененности рельефа местности // Известия ВУЗов. Геодезия и Аэрофотосъемка. — М.: 1978. — № 4. — С.13–23.
3. Крылов Н. Н., Иконникова Г. С., Николаев В. Л., Лаврухина Н. М. Начертательная геометрия. Учеб. для ВУЗов. — М.: Высшая школа, 1990. — С.79–103.
4. Фролов С. А. Начертательная геометрия. — М.: Машиностроение, 1978. — С.30–92.
5. Климухин А. Г. Начертательная геометрия. Учеб. для ВУЗов. — М.: Стройиздат, 1973. — С.50–92.

