В работе рассматриваются некоторые алгоритмы нестрого сопоставления строк как ключевой части алгоритмов нестрогого сопоставления записей баз данных, содержащих персональные данные, применительно к задаче исключения дублирования персональных данных.
В современных поисковых системах применяется поиск по ключевым словам (терминам), все методы которого можно разделить на три группы: поиск на точное соответствие, поиск с учетом изменяемости слова и нестрогий поиск. В данной работе мы рассматриваем нестрогий поиск.
Нестрогий поиск является методом поиска строк, которые соответствуют шаблону приблизительно, а неточно, что позволяет находить строки с ошибками.
Рассмотрим следующие алгоритмы нестрогого поиска:
- хеширование по сигнатуре;
- БК-дерево.
Алгоритм хеширование по сигнатуре (ХС) сначала был описан Бойцовым Л.М [1, 2,3] и до сих пор остается наиболее распространенным методом поиска, допускающим неточное задание терминов запроса. Это простой и очень эффективный алгоритм для работы в больших коллекциях строк.
Пусть задан непустой алфавит ![]() и известны вероятности появления различных символов алфавита. Пусть также на множестве символов
и известны вероятности появления различных символов алфавита. Пусть также на множестве символов ![]() задана функция
задана функция ![]() , отображающая буквы в числа от 1 до m. Эта функция, как несложно видеть, задает разбиение алфавита на m подмножеств.
, отображающая буквы в числа от 1 до m. Эта функция, как несложно видеть, задает разбиение алфавита на m подмножеств.
Определение. Сигнатурой ![]() слова
слова ![]() будем называть вектор размерности m, k-ый элемент которого равняется единице, если в слове
будем называть вектор размерности m, k-ый элемент которого равняется единице, если в слове ![]() есть символ
есть символ ![]() такой, что
такой, что![]() , и нулю в противном случае. Номером сигнатуры слова будем называть число
, и нулю в противном случае. Номером сигнатуры слова будем называть число ![]() . [2]
. [2]
![]() является хеш-функцией, отображающей множество слов в отрезок целых чисел от 0 до
является хеш-функцией, отображающей множество слов в отрезок целых чисел от 0 до ![]() , что позволяет организовать словарь в виде хеш-таблицы.
, что позволяет организовать словарь в виде хеш-таблицы.
Пусть слово ![]() получено из
получено из ![]() в результате одной операции редактирования: замены, добавления (удаления) или перестановки символов. Битовые векторы
в результате одной операции редактирования: замены, добавления (удаления) или перестановки символов. Битовые векторы ![]() и
и ![]() отличаются не более чем в одном разряде в случае операции добавления (удаления), и не более чем двух разрядах — в случае замены. Несложно также видеть, что, если при замене символов изменяются два элемента сигнатуры, то общее количество единиц остается неизменным, а произвольные перестановки, вообще, не влияют на сигнатуру.
отличаются не более чем в одном разряде в случае операции добавления (удаления), и не более чем двух разрядах — в случае замены. Несложно также видеть, что, если при замене символов изменяются два элемента сигнатуры, то общее количество единиц остается неизменным, а произвольные перестановки, вообще, не влияют на сигнатуру.
Метод хеширования по сигнатуре обладает следующими достоинствами:
- позволяет осуществлять с высокой скоростью поиск на точное равенство и поиск, допускающий одну-две «ошибки» в задании поискового запроса;
- ХС эффективно, как в случае «прямых» чтений с диска, так и из кэша;
- ХС использует компактный индекс. При правильном выборе параметров объем индекса не более чем на 10–20 % превышает размер файла, содержащего список терминов;
- отличается простотой реализации.
ХС присущ и один довольно существенный недостаток: он медленно работает, если индекс фрагментирован: то есть в том случае, если списки слов с одинаковыми сигнатурами разбросаны по несмежным секторам на диске. В настоящее время это не является большой проблемой, потому что, с одной стороны, размеры памяти компьютера часто позволяют загрузить словарь целиком, а с другой стороны, дефрагментация словаря, как правило, осуществляется в течение нескольких минут.
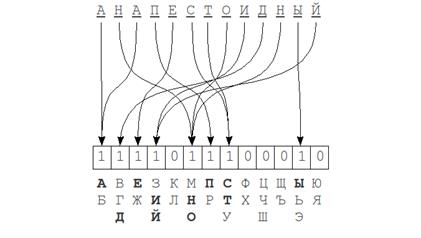
Процесс вычисления хеша: каждому биту хеша сопоставляется группа символов из алфавита. Бит 1 на позиции i в хеше означает, что в исходном слове присутствует символ из i-ой группы алфавита. Порядок букв в слове абсолютно никакого значения не имеет.
|
Хеш |
Список слов |
|
0000000000000 |
– |
|
• • • | |
|
1111011100001 |
АВТОПРЕДПРИЯТИЕ, БЕЗОТРАДНАЯ, БЕРЕРИНАРИЯ, • • • |
|
1111011100010 |
ПРЕВРАТНЫЙ, БЕЗРАССУДНЫЙ, АНАПЕСТОИДНЫЙ, • • • |
|
1111011100011 |
СОРИЕНТИРОВАТЬСЯ, БЕСПРЕПЯТСТВЕННЫЙ, • • • |
|
1111111111111 |
ЛЕГКОИСЧЕРПЫВАЮЩИХСЯ, ВЫСОКОРАЗРЕШАЮЩИХ, • • • |
Удаление одного символа либо не изменит значения хеша (если в слове еще остались символы из той же группы алфавита), либо же соответствующий этой группе бит изменится в 0. При вставке, аналогичным образом либо один бит встанет в 1, либо никаких изменений не будет. При замене символов хеш может либо вовсе остаться неизменным, либо же изменится в 1 или 2 позициях. При перестановках никаких изменений и вовсе не происходит, потому что порядок символов при построении хеша, как и было замечено ранее, не учитывается. Таким образом, для полного покрытия k ошибок нужно изменять не менее 2k бит в хеше. Время работы, в среднем, при k «неполных» (вставки, удаления и транспозиции, а также малая часть замен) ошибках:![]() .
.
Далее рассмотрим алгоритм BK-деревья [4, 5]. Деревья Баркхарда-Келлера являются метрическими деревьями, алгоритмы построения таких деревьев основаны на свойстве метрики отвечать неравенству треугольника:
![]()
Это свойство позволяет метрикам образовывать метрические пространства произвольной размерности. Такие метрические пространства не обязательно являются евклидовыми, так, например, метрики Левенштейна и Дамерау-Левенштейна образуют неевклидовы пространства. На основании этих свойств можно построить структуру данных, осуществляющую поиск в таком метрическом пространстве, которой и являются деревья Баркхарда-Келлера.
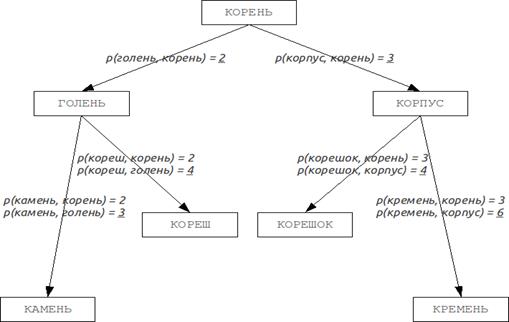
Улучшения:
Можно использовать возможность некоторых метрик вычислять расстояние с ограничением, устанавливая верхний предел, равный сумме максимального расстояния к потомкам вершины и результирующего расстояния, что позволит немного ускорить процесс:
![]()
Описанные выше алгоритмы были реализованы для сравнения скорости их работы. Реализаця выполнена на плтформе.NET Framework 3.5 и языке С#. Тестирование осуществлялось на компьютере с Intel Core i7 (2.93GHz), 6Gb ОЗУ, ОС –Windows 7 SP1.
Время работы алгоритмов:
|
Кол-во записей |
Кол-во потоков |
Время работы алгоритмов (с) | ||
|
Хеширование |
БК–дерево |
Полный–перебор | ||
|
1000 |
1 |
0,019 |
0,13 |
9,6 |
|
2 |
0,016 |
0,09 |
4,96 | |
|
5000 |
1 |
0,45 |
1,06 |
248,22 |
|
2 |
0,33 |
0,57 |
124,58 | |
|
10000 |
2 |
0,56 |
1,34 |
494,24 |
|
4 |
0,4 |
0,86 |
289,15 | |
В таблице результатов показано время работы алгоритмов в сравнении с алгоритмом полного перебора. Заметим, что реализованные алгоритмы работают во много раз быстрее чем полный перебор всех элементов.
Чтобы оценить эффективность работы реализованных алгоритмов, мы провели тесты на большом количестве строк (до миллиона).(с 1–10 тыс. приведено выше).
|
Кол-во строк (тыс.) |
Кол-во потоков |
Время работы (с) | |
|
Хеширование |
БК–дерево | ||
|
50 |
2 |
11,56 |
10,33 |
|
4 |
7,21 |
6,2 | |
|
100 |
2 |
45,7 |
25,13 |
|
4 |
27,86 |
14,67 | |
|
200 |
4 |
106,86 |
61,43 |
|
6 |
97,16 |
36,01 | |
|
500 |
4 |
48,17 |
114,24 |
|
6 |
44,64 |
99,67 | |
|
1000 |
4 |
185,08 |
252,29 |
|
6 |
168,5 |
222,47 | |
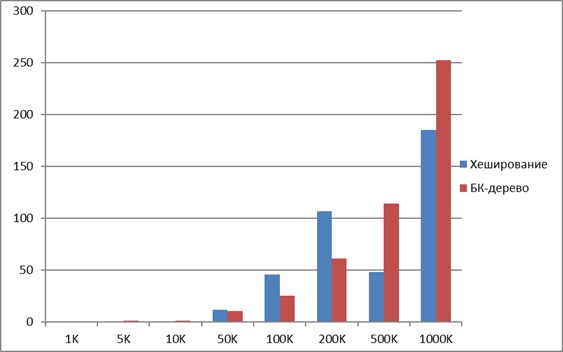
График приведен ниже. Заметим, что с меньшим количеством строк (до двухсот тысяч), БК–дерево работает быстрее чем хеширование. Но с увеличением количества строк хеширование оказывается эффективнее, т.к количество операций автоматически уменьшается на 1 для каждой сравнительной строки.
Проведенные исследования дают возможность сделать вывод, что для большой базы данных оба алгоритма, рассмотренные высшее, работают достаточно быстро и эффективно. Они дают возможность нахождения больших количеств дубликатов с большой вероятностью за допустимое время. Применение этих алгоритмы на практике позволит сократить время поиска и уменьшить время отклика программного обеспечения.
Литература:
1. Бойцов Л. М. Классификация и экспериментальное исследование современных алгоритмов нечеткого словарного поиска [текст] // Электронные библиотеки: перспективные методы и технологии, электронные коллекции: RCDL2004: тр. 6-й Всеросс. науч. конф. URL: http://www.rcdl.ru/papers/2004/paper27. pdf (дата обращения: 10.01.10).
2. Бойцов Л. М. Поиск по сходству в документальных базах данных: хеширование по сигнатуре оптимальное соотношение скорости поиска, простоты реализации и объема индексного файла. [текст]. // Программист. — 2001. — N 1. http://itman.narod.ru/articles/articles_fz_search.html#p8
4. http://en.wikipedia.org/wiki/BK-tree. [Электронный ресурс].
5. http://hamberg.no/erlend/posts/2012–01–17-BK-trees.html. [Электронный ресурс].

