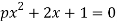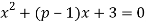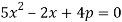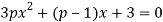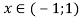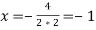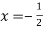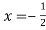Особенности системы задач на исследование расположения корней квадратного трёхчлена при обучении учащихся основной школы решению задач с параметром



В статье автор раскрывает особенности построения системы задач на исследование расположения корней квадратного трехчлена, способствующих формированию у учащихся основной школы умения решать задачи с параметром.

Актуальность вопроса формирования у учащихся умения решать задачи с параметром очевидна. Задачи с параметром являются составляющей ЕГЭ математики профильного уровня, некоторых олимпиадных задач, сам же параметр является основой модели многих реальных процессов. Ценность задач с параметром состоит в исследовании вариативности решения, его обобщении, что, безусловно, оказывает влияние на формирование предметных способов действий на качественно новом уровне и универсальных учебных действий учащихся в целом.

Знакомство учащихся с параметром начинается в курсе алгебры основной школы. Впоследствии, расширяется круг задач с постепенным ростом уровня сложности, уделяется внимание вариативным, нестандартным методам решения задач с параметром.

Основой решения многих задач с параметром является квадратный трёхчлен. В курсе алгебры основной школы он определяется как самостоятельная дидактическая единица, изучаются его свойства и применение в решении задач на: 1) поиск значения параметра, при котором уравнение имеет определённое количество корней; 2) доказательство существования такого параметра, при котором квадратное уравнение имеет только один корень или не имеет корней. В то же время, анализ учебников алгебры констатировал недостаточное количество задач на исследование квадратного трехчлена.

Вместе с тем, исследование учебно-методической литературы также позволило выявить следующие противоречия между: 1) ограниченностью программы школьного курса, что не позволяет в полном объеме рассмотреть решение квадратных уравнений, содержащих параметр, и частотой применения данной темы в материалах ОГЭ, ЕГЭ, вступительных испытаниях в различные учебные заведения; 2) обширностью теоретических знаний о квадратном трёхчлене и недостаточностью методических рекомендаций к обучению решению квадратных уравнений с параметрами.

В теории и методике обучения математике выделяются два подхода к изучению задач с параметрами:

1) постепенное введение понятия параметра и связанных с ним задач. В курсе алгебры присутствует ряд задач с параметром, которые традиционно отмечаются в темах учебника как задания повышенного уровня сложности. Данный подход предполагает решение учащимися заданий с параметром на протяжении всего изучения темы, либо проведение урока решения задач с параметром на одном из этапов изучения учащимися темы;

2) «погружение» в тему. Такой подход предполагает разработку программы курса по выбору, учебного модуля по исследуемой теме, начиная от введения понятия параметра и заканчивая изучением сложных комплексных задач. Существенными плюсами такой организации обучения является то, что разработанный курс, модуль, можно реализовать и в рамках первого подхода, а также расширить его для более сложных тем, например, решения заданий с параметром из второй части ЕГЭ по математике профильного уровня.

Выбор второго подхода, с одной стороны, обеспечит системное обучение решению задач на протяжении определенного временного промежутка, с другой стороны, курс, модуль будет изучен отдельной группой учащихся, интересующихся математикой. Тем не менее, исследование показывает преимущественный выбор учителями именно этого подхода.

Раскроем особенности задач на исследование квадратного трехчлена, способствующих более эффективному обучению учащихся основной школы решению задач с параметром.

Система упражнений, согласно исследованиям ученых-методистов [1, 6], должна отвечать принципам системности, полноты, вариативности, цикличности, непрерывного повторения, единственного различия. С позиции полноты целесообразно рассмотреть все варианты задач с параметром. В литературе представлены следующие классификации задач с параметром:

1) в зависимости расположения параметра в квадратном трехчлене. В этом случае решение квадратного уравнения будет строиться в соответствии с приведенными в таблице 1 указаниями:

Таблица 1

№	Место расположения параметра	Пример	Указания к решению
1	Коэффициент при старшей степени		1) Найти значение параметра, которое приводит к получению линейной функции. Решить полученный случай. 2) Решить квадратное уравнение, найти значение параметра согласно заданному условию.
2	Коэффициент при первой степени		Решить квадратное уравнение, найти значение параметра согласно заданному условию.
3	Свободный член		Решить квадратное уравнение, найти значение параметра согласно заданному условию.
4	В нескольких коэффициентах		1) Найти значения параметра, приводящие к понижению степени уравнения. Решить полученные случаи. 2) Решить квадратное уравнение, найти значение параметра согласно заданному условию.

2) в зависимости от формулировки самого задания: решение уравнений и неравенств в зависимости от значений параметра; нахождение значений параметра, для которых уравнение имеет заданное количество решений; нахождение значений параметра, для которых множество решений уравнений или неравенств обладает заданной характеристикой.

Как было сказано выше, имеющаяся система упражнений является недостаточной и должна, на наш взгляд, быть дополненной специальным образом сконструированными заданиями. Приведем примеры таких заданий.

Решение уравнений по алгоритму

1) Определите, при каком значении параметра уравнение имеет два различных корня, следуя алгоритму:

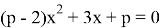
1. Записать выражение для дискриминанта через параметр.
2. Наложить на выражение ограничение, в зависимости от требования задачи.
3. Решить полученное уравнение или неравенство.
4. Записать ответ.

2) Заполните таблицу и определите, при каких значениях параметра a корни уравнения принадлежат интервалу (-1; 1).

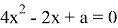
Шаг	Решение
1. Определить, при каких значениях параметра a уравнение имеет действительные корни.
2. Выразить корни уравнения через параметр для случая «D>0». Для случая D=0 подсчитать корень и проверить его принадлежность к интервалу.
4. Наложить условие на полученные корни.
5. Решить полученные на шаге 4 двойные неравенства.
4. Объединить полученные решения. Записать ответ.

Особенностью таких заданий является их расширенная формулировка, содержащая алгоритм как основу поэтапного выполнения учащимися математических действий. Принципы расширения формулировки заданий подробно описаны в исследовании Н. И. Трояновской [7]. Данные задания целесообразно предлагать учащимся на содержательном этапе урока изучения нового, когда алгоритмы решения только были «открыты» учащимися.

Практика выполнения подобных заданий способствует более прочному формированию умения выполнять задания с параметром.

Решение с пропусками

Заполните пропуски в решении квадратного уравнения с параметром :

1. При _________ получаем линейное уравнение ________, корнем которого является x=1.

2. При , получаем квадратное уравнение, дискриминант которого равен D=_____________________________________________.

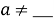
3. При D__0 параметр a____ и уравнение имеет 2 корня:

,

___________.

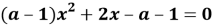
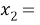
4. При D__0 параметр a ___ и уравнение имеет 1 корень:

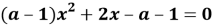
x=__________.

5. При D__0 уравнение не имеет корней.

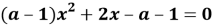
Ответ:______________________________________________________.

Указанное задание целесообразно применять на этапе рефлексии, для закрепления в памяти учащихся шагов изученных алгоритмов. Подобные задания становятся своего рода путеводителями в решении заданий с параметром и позволяют учащимся провести полное исследование корней уравнения в зависимости от контрольного значения параметра.

Поиск ошибки

После экзамена девятиклассники Маша и Саша решили обсудить решение предложенного ОГЭ задания:

Найдите все значения параметра a, при которых уравнение

имеет один корень? Найдите соответствующий (-щие) корень (корни).

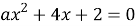
Между ребятами разгорелся жаркий спор, о том, чьё же решение всё-таки верное. Рассмотрите их работы и определите, кто не получит баллы за это задание и почему?

Критерий	Балл
Рассмотрен частный случай, приводящий к понижению степени уравнения и приведено полное решение уравнения. Указаны ответы (2 ответа) для всех значений параметра	2
Не рассмотрен частный случай приводящий к понижению степени уравнения. Приведено общее решение уравнения. Указан один ответ.	1
Не приведено решение. Или решение полностью неверное	0

Решение Маши:

1)D=16-8a 2) Уравнение имеет один корень, если D=0 16-8a=0 a=2 3) При a=2, Ответ: a=2, x= -1.

Решение Саши:

1) При а=0 уравнение принимает вид: 4x+2=0, тога 2)Пусть a 0, тогда найдём дискриминант квадратного уравнения: D=16-8a 3) Уравнение имеет один корень, если D=0 16-8a=0 a=2 4) При a=2, Ответ: при a=0, , при a=2, x= -1

Задание можно предлагать на этапе рефлексии уроков различного типа. Рассмотренное упражнение способствует формированию действий самоконтроля и взаимоконтроля у школьников, а также проработке ошибкоопасных мест в решении квадратных уравнений с параметром. С методикой построения заданий на поиск ошибки можно подробно ознакомиться в работе Н. И. Трояновской [7].

Диалоговые задания

При каких значениях параметра a уравнение имеет один корень?

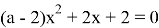
Письменно ответьте на вопросы:

1. При каких значениях параметра a данное квадратное уравнение обращается в линейное?____________________________________________
2. Запишите, чему равен дискриминант уравнения через параметр a: _______________________________________________________________
3. Чему равен дискриминант при получении только одного корня?___________________________________________________________
4. Запишите полученное условие для дискриминанта: _________________________________________________________________
5. Чему должен быть равен параметр a для выполнения полученного условия? _____________________________________________
6. Можем ли подставить полученное значение параметра в уравнение и решить его____________________________________________
7. Какой корень уравнения получится при найденном a? ________________________________________________________________
8. Сколько ответов у нас получилось? Запишите полученные ответы: _________________________________________________________

Диалоговые задания способствуют самостоятельному «открытию» учащимися алгоритмов действий, являются средством сопровождения ученика в освоении алгоритма решения задач с параметром. С методикой конструирования диалоговых заданий также можно подробно ознакомиться в исследовании Е. С. Квитко [3].

Задания на поиск особых значений параметра

При каких значениях параметра p следующие квадратные уравнения преобразуются в линейные? Решите полученные уравнения.

a)

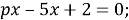
б)

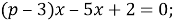
в)

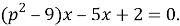
Такие задания помогают ученикам осознавать то, что некоторые значения параметра приводят к понижению степени уравнения и ведут к приобретению посторонних корней. Это задание способствует поиску учащимися ошибкоопасных мест в решении задач с параметром и провоцирует на продумывание действий во избежание ошибок.

Практикоориентированные задания

Перевозка тонны груза из пункта А в пункт В по железной дороге обходится на 10 рублей дороже, чем водным путём. Сколько тонн груза можно перевезти от А до В по железной дороге на сумму a рублей, если водным путём на эту же сумму можно перевезти на 8 тонн больше, чем по железной дороге?

Задания подобного типа позволяют ученикам осознавать связи темы с реальными жизненными ситуациями, способствуют формированию умения создавать математическую модель для конкретной задачной ситуации, развивают у учащихся познавательные универсальные учебные действия (обобщение, абстрагирование, анализ и синтез), определяют практическую значимость параметра — обобщение класса похожих практических ситуаций.

Обучение решению задач с параметром осуществляется более эффективно через «погружение» в тему. При этом система задач должна отвечать принципам системности, полноты, вариативности, цикличности, непрерывного повторения, единственного различия и содержать задания с учетом расположения параметра в квадратном трехчлене и вариативности формулировки самого задания (решение уравнений и неравенств в зависимости от значений параметра; нахождение значений параметра, для которых уравнение имеет заданное количество решений; нахождение значений параметра, для которых множество решений уравнений или неравенств обладает заданной характеристикой).

Вместе с тем эта система должна быть дополнена специальным образом сконструированными заданиями: решение уравнений по алгоритму, решение уравнений с пропусками, на поиск ошибок, поиск особых значений параметра, диалоговыми и практико-ориентированными заданиями.

В этом случае, как показало опытно-экспериментальное исследование, освоение алгоритмов решения квадратных уравнений с параметром происходит на качественно новом уровне.

Литература:

1. Иванова Т. А., Перевощикова Е. Н., Кузнецова Л. И., Григорьева Т. П. Теория и технология обучения математике в средней школе: Учеб. пособие для студентов математических специальностей педагогических вузов/ Под ред. Т. А. Ивановой. 2-е изд., испр. и доп. — Н. Новгород: НГПУ, 2009. 355 с.
2. Квитко Е. С. Методика обучения математике в 5–6 классах, ориентированная на формирование универсальных учебных действий: дисс. канд. пед. наук — Москва, 2014. — 174 с.
3. Колягин Ю. М., Ткачева М. В., Федорова Н. Е., Шабунин М. И. Алгебра. 8класс: учеб. для общеобразоват. организаций/ Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. — М.: Просвещение, 2017–336с.: ил.
4. Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений/ 16-e издание, дополненное — М.: Мнемозина, 2016.
5. Мугаллимова С. Р. Учим решать уравнения и неравенства с параметром// Научно-методический электронный журнал «Концепт». — 2016. — № 7 (июль). — 0,5 п.л. — URL: http://e-koncept.ru/2016/16140.htm.
6. Саранцев Г. И. Упражнения в обучении математике / Г. И. Саранцев. — 2-е изд., дораб. — М.: Просвещение, 2005. — 254с.
7. Трояновская Н. И. Технология формирования действий контроля и оценки учащихся 5–6 классов в обучении математике: дисс. канд. пед. наук–Нижний Новгород, 2015. –228 с.
8. Усманова И. И., Виталова С. Л. Обучение решению задач на исследование расположения корней квадратного трёхчлена [Текст]/ И. И. Усманова, С. Л. Виталова// Международный журнал экспериментального образования. — 2014. — № 7 (часть 1) — С. 84–86.