В статье рассматриваются различные особенности сеточных уравнений; различные методы решения сеточных уравнений.
Ключевые слова: сеточные уравнения, разностные уравнения, численные методы, линейная алгебра, вариационные методы, оптимальное решение.
Использование различных численных методов (разностных, переменно-разностных, проекционно-разностных методов, в том числе метода конечных элементов) приводит к системе линейных алгебраических уравнений специального вида — разностных уравнений [1]. Эта система имеет следующие особенности:
1) имеет более высокий порядок, чем количество узлов сетки;
2) система не является условной (отношение максимального значения матрицы системы к минимальному велико; например, для разности оператора Лапласа это отношение обратно пропорционально квадрату степени сетки);
3) матрица системы разреженная — каждая ее строка имеет несколько ненулевых элементов, не зависящих от числа узлов;
4) ненулевые элементы матрицы располагаются в специальном месте — лента становится матрицей.
Большое количество физических и технических задач приводят к дифференциальным уравнениям частных производных (уравнениям математической физики). Различные физические природные процессы описываются уравнениями эллиптической формы.
Точные решения краевых задач для эллиптических уравнений могут быть получены лишь в частных случаях. Поэтому эти задачи в большинстве случаев решаются приближенно. Одним из наиболее универсальных и эффективных методов, широко используемых в настоящее время для приближенного решения уравнений математической физики, является метод конечных разностей или метод сеток.
Область непрерывного изменения аргументов (например, отрезок, прямоугольник и т. д.) заменяется отдельными точками (узлами), называемыми ячейками. Вместо непрерывного аргумента мы рассматриваем функции отдельных аргументов, определенные в узлах сетки и называемые функциями сетки. Производные и граничные условия, введенные в дифференциальное уравнение, заменяются разностными производными; в этом случае краевая задача для дифференциального уравнения заменяется системой линейных или нелинейных алгебраических уравнений (петлевых или разностных уравнений). Такие системы часто называют разностными схемами.
Пусть
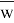
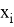
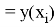
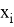
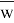
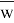
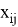
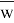
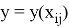
Посмотрим на сетку в двумерной области:
Пусть
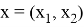
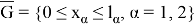
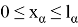
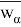
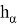
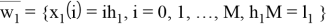
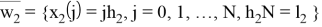
Набор узлов
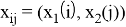
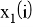
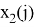
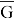
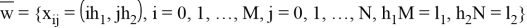
Сетка
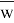
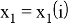
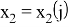
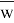
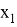
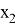
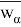
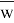
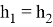
Точки
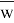
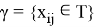
Для описания структуры сетки
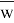
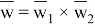
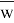
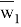
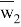
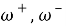
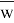
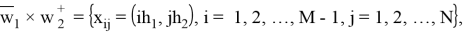
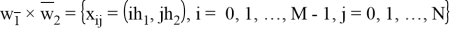
Давайте посмотрим на концепцию сеточной функции. Пусть
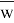
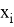
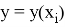
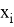
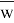
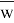
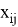
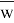
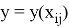
При сходимости сеточного интегрального и интегро-дифференциального уравнений мы получаем систему уравнений с заданной функцией-сетки (сеточной функции). Такие уравнения еще называют сеточными уравнениями и имеют следующий вид:
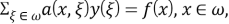
Здесь суммирование производится по всем узлам ячейки, то есть по множеству дискретных точек. Матрица сеточного уравнения
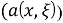
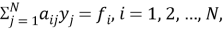
здесь i, j — номера узлов сетки, а N — общее количество узлов. Противоположная линия мышления очевидна. Таким образом, линейное сеточное уравнение представляет собой систему линейных алгебраических уравнений, и наоборот, любую линейную систему алгебраических уравнений можно рассматривать как линейное уравнение, связывающее сеточную функцию, заданную числом узлов, равным порядку системы. Вариационные методы (Ритц, Галеркин и др.) численного решения дифференциальных уравнений обычно приводят к системам с заполненными матрицами [2].
Понятно, что решение сетки, и особенно разностных уравнений, представляет собой задачу линейной алгебры.
Существует множество методов решения задач линейной алгебры, ведется непрерывная работа по их совершенствованию, пересматриваются и разрабатываются новые методы. Следовательно, значительное количество существующих методов имеют право на существование и имеют области применения. Поэтому для решения той или иной задачи в вычислительной технике возникает проблема выбора одного метода из множества приемлемых методов решения этой задачи. Этот метод должен обладать лучшими особенностями, такими как минимальное время решения задачи на компьютере (или минимальное количество арифметических и логических операций при нахождении решения) (или, как говорят, он должен быть оптимальный метод), вычислительная устойчивость, т. е. ошибки округления, относительная стабильность и т. д.
Любой вычислительный алгоритм для компьютера требует, чтобы решение заданной задачи осуществлялось с определенной ε > 0 точностью за конечное число ходов Q(ε). Этому требованию удовлетворяет бесконечное множество алгоритмов, которые должны найти хотя бы алгоритм Q(ε) для любого ε > 0. Такой алгоритм называется эффективным. Разумеется, поиск «оптимального» или «лучшего» метода осуществляется среди множества известных методов, а сам термин «оптимальный алгоритм» имеет ограниченное и условное значение.
Цель теории численных методов — найти лучшие алгоритмы для данного класса задач и создать иерархию методов. Само понятие зависит от цели расчетов.
Задача выбора оптимального метода имеет две возможные постановки:
-
решение некоторой системы уравнений с матрицей
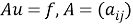
- требуется решить несколько версий одной и той же задачи, например, решить уравнение Au = f с разными f правыми частями.
Вместо пересчета каждого варианта (например, обратной матрицы) вы можете уменьшить среднее количество прогонов Q (ε) для каждого варианта, если сохраните некоторые значения.
Понятно, что это зависит от способности компьютера хранить в своей памяти дополнительную информацию, которая, в свою очередь, зависит от типа компьютера и расположения системы уравнений.
Литература:
- Самарский А. А., Карамзин Ю. Н. Разностные уравнения. — Москва: Знание, 1978.
- Пименов В. Г., Ложников А. Б. численные методы. — Екатеринбург, Издательство Уральского университета, 2014.







