Достоверный расчет несущих конструкций является основой при их оптимизации. Одним из путей уменьшения трудоемкости, материалоемкости и стоимости дощатоклееных рам является выбор их оптимальных параметров — уклона ригеля и шага. Целесообразность проведения такого исследования очевидна, так как будет способствовать расширению применения этих, конструкций в строительстве.
Вышеуказанный комплекс взаимосвязанных вопросов определил основную цель работы, которая заключается в экспериментально-теоретическом исследовании напряженно-деформированного состояния рам типа ДГРП с целью совершенствования расчета на прочность и выбор оптимальных параметров рам, применительно к габаритным размерам зданий.
Для разрешения изложенных выше и сопряженных с ними задач в настоящей работе поставлены следующие цели исследования:
- теоретически исследовать напряженно-деформированное состояние рам
- выполнить сравнительный анализ одно и трех шарнирных рам.
- смоделировать и сравнить полученные результаты с результатами ранее проведенного экспериментального исследования в диссертации Табунова С. Ю.«Расчет и выбор оптимальных параметров РАМ с прямолинейным ригелем и гнутоклееными стойками для сельскохозяйственных зданий» [1]
- провести оценку поученных результатов и дать рекомендации по проектированию и расчету клееных рам.
Выбор формы и размеров исследуемой рамы
Методикой предусматривалось расчет различных рам методом конечных элементов основные размеры рам приняты из условия предварительных расчетов рам: высота сечения рам назначается в пределах 1/12... 1/30 пролета рам. Высота поперечного сечения ригеля рам в коньковом узле принимается не менее 0,3 h, а в опорном сечении — не менее 0,4 h.
Прямолинейные элементы рам изготавливаются из слоев толщиной после острожки 32 мм. Толщина слоев в гнутоклееных рамах зависит от внутреннего радиуса кривизны в карнизном узле и назначается в пределах 16...24 мм (см. табл. 8 СНиП [8]).Радиус гнутого узла принимается в пределах 2м — 4м.
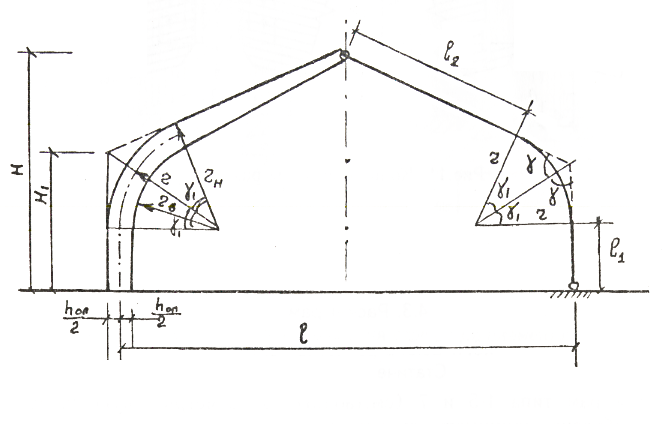
Основные параметры гнутоклееной рамы показаны на рис. 1.
Рис. 1 Деревянная гнутоклееная рама
Расчет выполнен с помощью проектно-вычислительного комплекса SCAD. Комплекс реализует конечно-элементное моделирование статических и динамических расчетных схем, проверку устойчивости, выбор невыгодных сочетаний усилий, подбор арматуры железобетонных конструкций, проверку несущей способности стальных конструкций. В представленной ниже пояснительной записке описаны лишь фактически использованные при расчетах названного объекта возможности комплекса SCAD.
В основу расчета положен метод конечных элементов с использованием в качестве основных неизвестных перемещений и поворотов узлов расчетной схемы. В связи с этим идеализация конструкции выполнена в форме, приспособленной к использованию этого метода, а именно: система представлена в виде набора тел стандартного типа (стержней, пластин, оболочек и т. д.), называемых конечными элементами и присоединенных к узлам (рис 2)
Тип конечного элемента определяется его геометрической формой, правилами, определяющими зависимость между перемещениями узлов конечного элемента и узлов системы, физическим законом, определяющим зависимость между внутренними усилиями и внутренними перемещениями, и набором параметров (жесткостей), входящих в описание этого закона и др.
Рис. 2 Конечный элемент
Узел в расчетной схеме метода перемещений представляется в виде абсолютно жесткого тела исчезающее малых размеров. Положение узла в пространстве при деформациях системы определяется координатами центра и углами поворота трех осей, жестко связанных с узлом. Узел представлен как объект, обладающий шестью степенями свободы — тремя линейными смещениями и тремя углами поворота.
Все узлы и элементы расчетной схемы нумеруются. Номера, присвоенные им, следует трактовать только, как имена, которые позволяют делать необходимые ссылки.
Конечные элементы оболочек, геометрическая форма которых на малом участке элемента является плоской (она образуют многогранник, вписанный в действительную криволинейную форму срединной поверхности оболочки). Для этих элементов, в соответствии с идеологией метода конечных элементов, истинная форма перемещений внутри элемента приближенно представлена упрощенными зависимостями. Описание их напряженного состояния связано с местной системой координат, у которой оси X1 и Y1 расположены в плоскости элемента и ось Х1 направлена от первого узла ко второму, а ось Z1 ортогональна поверхности элемента.
Треугольный элемент типа 42, не является совместным и моделирует поле нормальных перемещений внутри элемента полиномом 4 степени, а поле тангенциальных перемещений полиномом первой степени. Располагается в пространстве произвольным образом.
Четырехугольный элемент типа 44, который имеет четыре узловые точки, не является совместным и моделирует поле нормальных перемещений внутри элемента полиномом 3 степени, а поле тангенциальных перемещений неполным полиномом 2 степени. Располагается в пространстве произвольным образом.
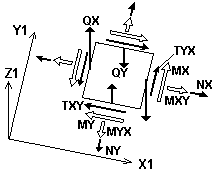
В конечных элементах оболочки вычисляются следующие усилия (рисунок 3):
нормальные напряжения NX, NY;
сдвигающее напряжений TXY;
моменты MX, MY и MXY;
перерезывающие силы QX и QY;
Рис.3 Конечный элемент
На рис.3 показаны положительные значения напряжений, перерезывающих сил и векторов моментов, действующие по граням элементарного прямоугольника, вырезанного в окрестности центра тяжести КЭ оболочки.
Основная система метода перемещений выбирается путем наложения в каждом узле всех связей, запрещающих любые узловые перемещения. Условия равенства нулю усилий в этих связях представляют собой разрешающие уравнения равновесия, а смещения указанных связей — основные неизвестные метода перемещений.
В общем случае в пространственных конструкциях в узле могут присутствовать все шесть перемещений:
1 — линейное перемещение вдоль оси X;
2 — линейное перемещение вдоль оси Y;
3 — линейное перемещение вдоль оси Z;
4 — угол поворота с вектором вдоль оси X (поворот вокруг оси X);
5 — угол поворота с вектором вдоль оси Y (поворот вокруг оси Y);
6 — угол поворота с вектором вдоль оси Z (поворот вокруг оси Z).
Нумерация перемещений в узле (степеней свободы), представленная выше, используется далее всюду без специальных оговорок, а также используются соответственно обозначения X, Y, Z, UX, UY и UZ для обозначения величин соответствующих линейных перемещений и углов поворота.
В соответствии с идеологией метода конечных элементов, истинная форма поля перемещений внутри элемента (за исключением элементов стержневого типа) приближенно представлена различными упрощенными зависимостями. При этом погрешность в определении напряжений и деформаций имеет порядок (h/L)k, где h — максимальный шаг сетки; L — характерный размер области. Скорость уменьшения ошибки приближенного результата (скорость сходимости) определяется показателем степени k, который имеет разное значение для перемещений и различных компонент внутренних усилий (напряжений).
Системы координат
Для задания данных о расчетной схеме могут быть использованы различные системы координат, которые в дальнейшем преобразуются в декартовы. В дальнейшем для описания расчетной схемы используются следующие декартовы системы координат:
Глобальная правосторонняя система координат XYZ, связанная с расчетной схемой
Локальные правосторонние системы координат, связанные с каждым конечным элементом.
Выбор типа расчетной схемы
Расчетная схема определена как система с признаком 5. Это означает, что рассматривается система общего вида, деформации которой и ее основные неизвестные представлены линейными перемещениями узловых точек вдоль осей X, Y, Z и поворотами вокруг этих осей.
Гнутоклееная деревянная рама представлена как трех шарнирная и одна шарнирная. Заданные правильные граничные условия, и приложена расчетная нагрузка. рассмотрены три комбинации загружений:
- Собственный вес(0.05 Т/м) + погонная нагрузка от покрытия (0.68 Т/м)+ снег на всю длину(0.54 Т/м)
- Собственный вес(0.05 Т/м) + погонная нагрузка от покрытия(0.68 Т/м) + снег слева(0.54 Т/м)
- Собственный вес(0.05 Т/м) + погонная нагрузка от покрытия (0.68 Т/м)+ снег справа(0.54 Т/м)
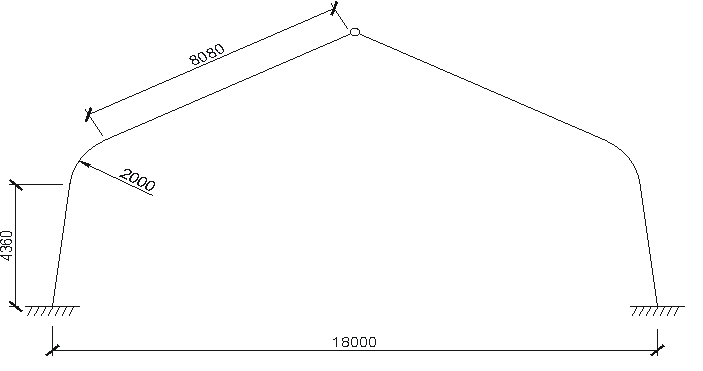
Рис. 4. Геометрические размеры рамы
При анализе результатов расчёта, было выяснено, что введение «лишних» связей, т. е. статической неопределимости в статическую работу рам, приводит к перераспределению усилий с наиболее напряженного участка (гнутой карнизной части) рамы в менее напряженные места. Учитывая то, что карнизная гнутая часть является наиболее ответственной, с точки зрения безопасности работы рамы, подобное явление благоприятно, поскольку позволяет при проектировании рамы уменьшить рабочее сечения в опасных участках и более надежно выполнить напряженный участок гнутой рамы.
Сравнивая величины максимальных изгибающих моментов, возникающих в одношарнирной и трехшарнирной рамах, можно отметить снижение расчетных усилий в наиболее опасном и напряженном сечении почти на 6 % Естественно что такое снижение максимального изгибающего момента в раме может привести к уменьшению высоты рабочего сечения почти на 50 %
Перераспределение изгибающего момента с карнизного узла на определенную часть стоек рамы, с другой стороны, может привести к увеличению высоты сечения стоек рамы в определенных участках. Однако следует заметить, что на этих участках отсутствует кривизна (что лучше для работы деревянного клееного элемента) и выравнивание высоты сечения рамы по длине ее снимет технологические трудности при выполнении переменности высоты сечения по длине рамы.
Считаем, что изменение статической схемы рамы, т. е. переход на рамы одношарнирные может дать в целом технико-экономический эффект как в расходе клееной древесины так и в трудозатрат при их изготовлении.
Литература:
- Расчет и выбор оптимальных параметров РАМ с прямолинейным ригелем и гнутоклееными стойками для сельскохозяйственных зданий: диссертация... кандидата технических наук Табунова С. Ю.: 05.23.01 61 85–5/236 Ленинград, 1984
- СНиП II-25–80, «Деревянные конструкции». М., Стройиздат, 1980г.