Задача прогнозирования свойств оксидных расплавов актуальна для самых разных областей науки и технологии, например, для геофизики (магматические расплавы), некоторых процессов выращивания монокристаллов, разработки энергетических агрегатов - топок с жидким шлакоудалением. Однако возможность прогнозирования физико-химических свойств оксидных расплавов (шлаков) особенно важна для технологий металлургической отрасли.
Одним из наиболее значимых свойств шлаков является вязкость, поскольку в основе многих металлургических процессов лежат явления, зависящие от характера тепло- и массопереноса в шлаковой фазе. В производственных условиях шлаки, как правило, гетерогенны, расплав содержит в себе то или иное количестве твердых частиц, оказывающих сильное влияние на вязкость. Поэтому на практике необходимую вязкость шлака получают, фактически, регулируя степень его гетерогенности. При этом используют эмпирические зависимости, отражающие только качественную сторону процесса и частные условия. Объективные трудности в описании свойств гетерогенных шлаков затрудняют разработку и применение научно обоснованных количественных зависимостей. Очевидно, это снижает возможности управляющих воздействий и эффективность технологий.
Средний химический состав гетерогенных шлаков не в полной мере характеризует их свойства. Для разработки адекватных моделей свойств необходимо иметь метод расчета распределения компонентов по фазам и количества фаз, отражающий природу гетерогенных шлаков. Подобный метод позволит оценивать их эффективную вязкость по данным о среднем химическом составе и температуре, используя зависимости, предложенные А. Эйнштейном и Я. Френкелем для вязкости суспензий [1, с. 488].
Возможность применения уравнения Эйнштейна (1) и его модификаций к шлакам обсуждалась в исследовании [2, с. 516]:
где, η – вязкость суспензии, ηо – вязкость жидкой фазы суспензии, ε – объёмная доля твёрдых частиц.
Авторы данного исследования проверили возможность использования диаграммы состояния CaO – SiO2 – FeOn для оценки эффективной вязкости гетерогенных шлаков этой системы путём определения количества твёрдых частиц и состава жидкой фазы из геометрических построений. Известный состав жидкой фазы позволял определять её вязкость ηо по моделям вязкости для гомогенных шлаков и рассчитать эффективную вязкость по уравнению (1) или его модификациям. Сопоставляя опытные значения вязкости гетерогенного шлака с расчётными, проверяли адекватность этих уравнений. Было отмечено удовлетворительное соответствие опытных данных и результатов расчётов по уравнению:
Возможность использования диаграмм состояния для расчётов эффективной вязкости определяется тем, что диаграмма состояния, по сути, является диаграммой растворимости [3, с. 246]. Поэтому диаграмму состояния можно рассматривать как «графически изображенную модель насыщения» для двух-, трёх- или, максимум, четырёхкомпонентной системы. Возможность расчета состава жидкой фазы и количества твердых частиц по диаграммам определяется тем, что известно положение линии ликвидус в координатах «состав – температура».
Очевидно, что диаграмма состояния в качестве «графически изображенной модели насыщения» менее практична, чем чисто многомерная аналитическая модель, которая позволила бы рассчитывать количество и состав фаз при равновесии с многокомпонентным расплавом при разных температурах. Методика определения количества фаз и их составов в аналитической модели может быть аналогична известной методике расчёта по диаграммам состояния, являясь её обобщением на случай многокомпонентных систем [4, с. 19].
В данной работе для оценки равновесного состава твердых и жидких фаз в шлаках предлагается использовать современный вариант полимерной модели строения шлаков [5, с. 10]. Полимерная теория строения шлака является дальнейшим развитием ионной теории. Её особенностью является учет наличия в расплаве не только простейших ионов, но также и крупных комплексных анионов, которые могут объединяться друг с другом, т.е. полимеризоваться. Причиной образования комплексных анионов является существенное различие ионных потенциалов катионов шлака, оценивающихся отношением заряда катиона к его размеру. Это различие приводит к тому, что наиболее «сильные» катионы, прежде всего, кремния, формируют вокруг себя стабильное окружение из анионов кислорода. Сила связи внутри этих комплексов больше, чем между этими анионами и окружающими катионами, что и позволяет выделять комплексы как отдельные структурные единицы расплава. Кроме того, в отличие от солевых систем простейшие анионы оксидных расплавов имеют заряд «-2», поэтому он может образовывать две связи с ближайшими катионами. Например, одну связь с катионом кремния, а другую - с катионом кальция или же обе связи с катионами кремния. В результате в зависимости от состава шлака, например, от содержания катионов кальция, возможно различное развитие процессов объединения кремнекислородных анионов (полимеризации). Исходя из учета этих процессов в полимерной модели строения оксидных расплавов рассчитывается ряд свойств шлаков и активности их компонентов.
Рассмотрим разработанный нами алгоритм
прогнозирования состава и количества фаз на примере, отражающем
аналогию алгоритма с методикой расчётов по диаграммам состояния
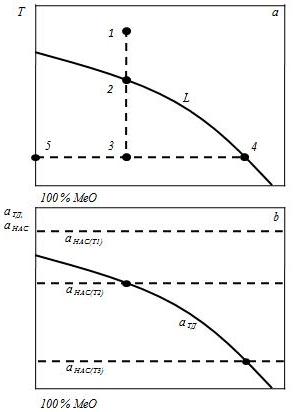
(рис.1). В точке 1, расположенной выше линии ликвидус L,
исходный расплав имеет соответствующие температуру и содержание
оксида MeO. Степень приближения расплава к
насыщению МеО в полимерной модели оценивается по соотношению двух
параметров: термодинамической активности МеО в расплаве
![]() ,
являющейся функцией состава расплава, и активности насыщения МеО
,
являющейся функцией состава расплава, и активности насыщения МеО
![]() ,
являющейся функцией температуры Т [5, с. 27].
,
являющейся функцией температуры Т [5, с. 27].
В точке 1, с соответствующей температурой Т1, справедливо неравенство, свидетельствующее о ненасыщенности расплава MeO (рис. 1а и 1b):
При понижении температуры от точки 1 до точки 2 (не включая саму
точку 2, лежащую на линии ликвидус L)
происходит снижение
![]() ,
однако
,
однако
![]() всё ещё превышает
всё ещё превышает
![]() .
В точке 2 активность насыщения MeO,
определяемая температурой Т2, достигает термодинамической
активности МеО в расплаве, что свидетельствует о насыщении расплава
МеО [5, с. 27]:
.
В точке 2 активность насыщения MeO,
определяемая температурой Т2, достигает термодинамической
активности МеО в расплаве, что свидетельствует о насыщении расплава
МеО [5, с. 27]:
Если и при дальнейшем снижении температуры от точки 2 до точки 3
считать, что состав исходного расплава не изменяется (не снижается
содержание МеО), то
![]() становится выше, чем, например,
становится выше, чем, например,
![]() .
Это говорит о том, что гомогенный расплав с исходным содержанием МеО
при температурах ниже ликвидуса существовать не может. Поэтому при
понижении температуры ниже ликвидуса начинается выделение МеО из
гомогенного расплава в таких количествах, чтобы при каждой
температуре соблюдалось равенство
.
Это говорит о том, что гомогенный расплав с исходным содержанием МеО
при температурах ниже ликвидуса существовать не может. Поэтому при
понижении температуры ниже ликвидуса начинается выделение МеО из
гомогенного расплава в таких количествах, чтобы при каждой
температуре соблюдалось равенство
![]() и
и
![]() ,
т.е. при понижении температуры от точки 2 до точки 3 изменение
состава гомогенного расплава происходит по линии 2-4 (рис.1а).
,
т.е. при понижении температуры от точки 2 до точки 3 изменение
состава гомогенного расплава происходит по линии 2-4 (рис.1а).
Рис. 1. Принципиальная схема расчёта количества твёрдых частиц в гетерогенном шлаке и состава его жидкой фазы, иллюстрирующая аналогию с методикой расчётов по диаграммам состояния:
а – участок гипотетической диаграммы состояния бинарного расплава в координатах «состав» - «температура»;
b – соотношение
термодинамической активности
![]() и активности насыщения оксида MeO
и активности насыщения оксида MeO
![]() в том же расплаве при изменениях температуры и состава расплава
в том же расплаве при изменениях температуры и состава расплава
Если рассматривать данный пример в виде части
диаграммы состояния (рис.1а), то массовую долю кристаллов МеО
и состав жидкой фазы шлака можно определить из графических построений
(линия 5-3-4) – эта возможность обусловлена известным
положением линии ликвидуса на диаграмме. Однако наличие графически
представленной линии ликвидус в координатах «состав -
температура» не обязательно, поскольку линия ликвидус
описывается равенством
![]() и
и
![]() ,
фактически задающих эти же координаты. Поэтому положение линии
ликвидус в координатах «состав - температура» может
определяться расчётом (рис.1b). Это
позволяет обобщить представленный выше алгоритм для многокомпонентных
шлаков, для которых не существует графически представленных диаграмм
состояния – графически изображённые поверхности ликвидус
равноценно заменяются уравнениями полимерной модели.
,
фактически задающих эти же координаты. Поэтому положение линии
ликвидус в координатах «состав - температура» может
определяться расчётом (рис.1b). Это
позволяет обобщить представленный выше алгоритм для многокомпонентных
шлаков, для которых не существует графически представленных диаграмм
состояния – графически изображённые поверхности ликвидус
равноценно заменяются уравнениями полимерной модели.
Таким образом, методика определения количества нерастворённых кристаллов и состава жидкой фазы гетерогенного шлака состоит в следующем:
- определение минимальной температуры, при которой для всех компонентов шлака термодинамические активности не превышают активностей насыщения (определяется температура ликвидус);
- уменьшение содержания тех компонентов в
расплаве, для которых по мере снижения температуры ниже ликвидуса
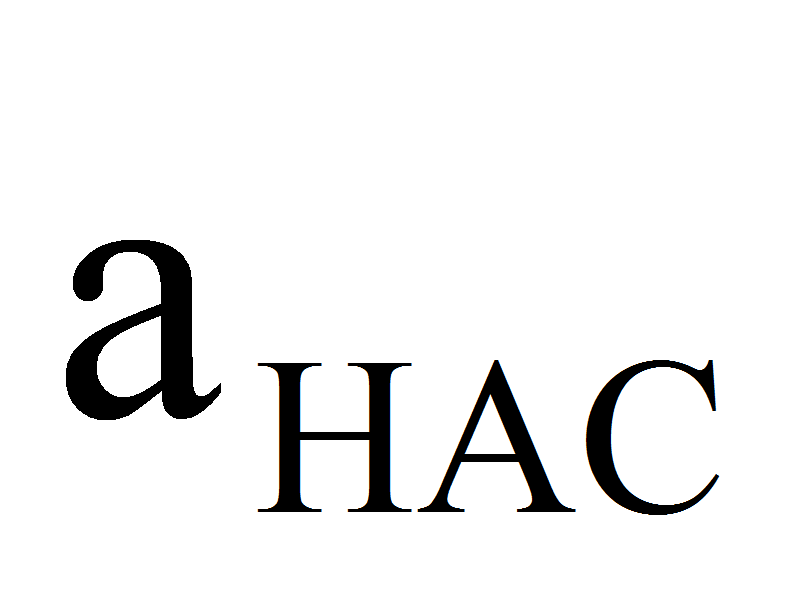 сравнивается с
сравнивается с
 ;
уменьшение содержания этих компонентов в расплаве производится таким
образом, чтобы при каждой температуре
;
уменьшение содержания этих компонентов в расплаве производится таким
образом, чтобы при каждой температуре
 была равна
была равна
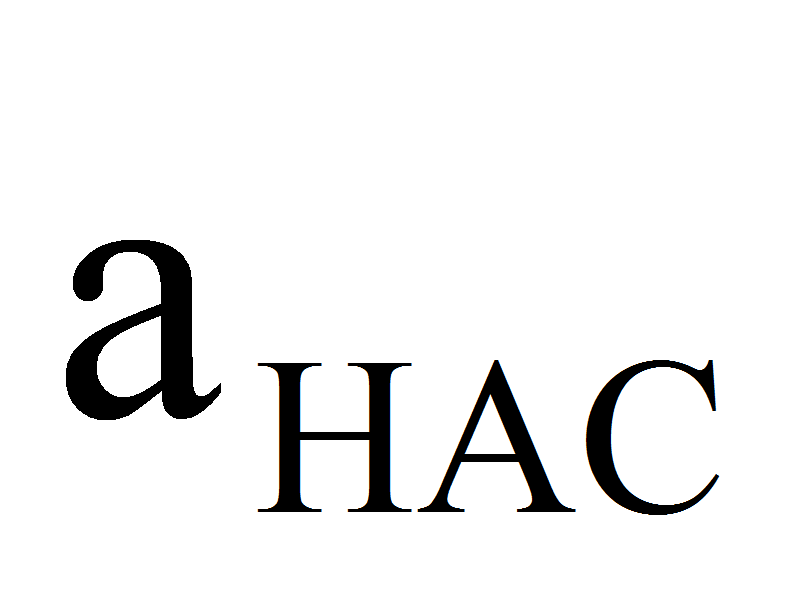 (рассчитывается состав жидкой фазы гетерогенного шлака);
(рассчитывается состав жидкой фазы гетерогенного шлака);
- определение массовой доли нерастворённых кристаллов по балансу компонентов исходного расплава при температуре ликвидус и состава жидкой фазы при его гетерогенизации.
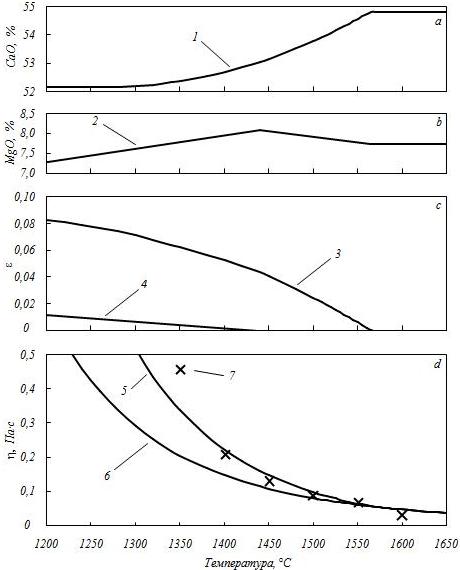
Известный состав жидкой фазы позволяет определить её вязкость η0 по моделям для гомогенных систем. Для пересчёта массовой доли твёрдой фазы в объёмную долю следует иметь данные о плотности твёрдых частиц и жидкой фазы шлака [2, с. 518]. Используя формулы вида (1) и (2) при имеющихся значениях вязкости жидкой фазы η0 и объёмной доли нерастворённых кристаллов ε, можно определять эффективную вязкость шлака η. Сопоставление опытных данных и результатов расчёта вязкости по представленной методике приведено на рисунке 2 для типичного шлака внепечной обработки стали (масс. %): СаО = 55,8 %; SiO2 = 23,6 %; MgO = 7,7 %; FeO = 1,5 %; A2O3 = 11,4 %.
Согласно расчетам по полимерной модели при снижении температуры ниже ликвидуса (1565°С) начинается уменьшение количества CaO в расплаве (рис.2а), что приводит к появлению в шлаке соответствующего количества кристаллов CaO (рис.2с). По мере снижения содержания CaO в жидкой фазе шлака происходит соответствующее повышение содержания остальных компонентов в жидкой фазе шлака, в том числе MgO (рис.2b). При температуре 1440°С жидкая фаза насыщается MgO, дальнейшее снижение температуры приводит к снижению содержания MgO в жидкой фазе (рис.2b) и появлению соответствующего количества кристаллов MgO (рис.2с). Поэтому при снижении температуры ниже ликвидуса вязкость шлака растёт быстрее, чем можно судить по расчетам, не учитывающим гетерогенизацию (рис.2d).
Необходимо отметить, что обоснованно использовать результаты расчётов по представленной методике для описания свойств реальных шлаков, можно только при сохранении ньютоновского характера их вязкого течения, т.е. при ε до 0,1 – 0,25 [2, с. 516]. Кроме того, выделившиеся кристаллы CaO и MgO могут поглощать оксиды железа и марганца из жидкой фазы шлака с образованием твердых растворов типа (Ca∙Fe∙Mn)O и (Mg∙Fe∙Mn)O, что должно оказывать влияние на результаты экспериментов по измерению вязкости [6, с. 26]. Чем больше в шлаке частиц CaO и MgO и чем дольше они существуют, тем больше эти частицы должны поглощать оксидов железа и марганца из жидкой фазы шлака, повышая вязкость жидкой фазы шлака и увеличиваясь в размерах.
Рис. 2. Температурные зависимости опытных значений вязкости η и промежуточных результатов её расчёта:
а – содержание СаО в жидкой фазе шлака (1);
b – содержание MgО в жидкой фазе шлака (2);
c – объёмная доля ε твёрдых частиц CaO в шлаке (3) и MgО (4);
d – значения вязкости, рассчитанные по полимерной модели с учётом гетерогенизации (5); значения вязкости, рассчитанные по полимерной модели без учёта гетерогенизации (6); опытные значения вязкости (7)
Результаты исследований позволяют считать, что разработанный подход к оценке вязкости гетерогенных шлаков допустимо использовать при решении ряда практических задач.
Литература:
- Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука, 1975. 487 с.
- Ito K., Fruehan R.J. // Metallurgical transactions. 1989. Vol. 20B. Pp. 515-521.
- Явойский В.И., Кряковский Ю.В., Григорьев В.П. и др. Металлургия стали: Учебник для вузов. М.: Металлургия,1983. 584 с.
- Воскобойников В.Г., Дунаев Н.Е., Михалевич А.Г. и др. Свойства жидких доменных шлаков. М.: Металлургия, 1975. 184 с.
- Новиков В.К., Невидимов В.Н. Полимерная природа расплавленных шлаков. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 62 с.
- Штенгельмейер С.В., Богатенков В.Ф. // Изв. вуз. Чёрная металлургия. 1958. № 11. С. 23-28.