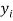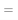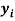Предложен и обоснован новый метод выявления зависимостей электроотрицательности (ЭО) атомов как функции от их расположения в периодах таблицы Д. И. Менделеева. Определен ряд закономерностей и представлены описывающие их математические выражения, позволяющие с высокой точностью рассчитать ЭО химического элемента, используя его местоположение в таблице Д. И. Менделеева. В основу данного метода положены общепринятые научные положения — факты, характеризующие основные свойства атомов. Разработанный метод базируется только на использовании наблюдаемых значений ЭО и их изменений в таблице. Изложенные в работе результаты позволили лишь частично, чисто формально, установить взаимозависимость между большей частью элементов таблицы. Кроме того, полученные результаты дали возможность еще раз убедиться в величии закона открытого Д. И. Менделеевым.
Ключевые слова : электроотрицательность (ЭО), шкала Оллреда-Рохова, опорные элементы, регрессионный анализ, метод наименьших квадратов,метрологические аспекты.
Настоящая работа формировалась и проводилась под влиянием феноменальных результатов исследования выдающегося математика и инженера Клода Эльвуда Шеннона, доказавшего, что принципиально возможно создавать надежные вычислительные системы из определенного множества ненадежных элементов, используя математические аппараты теории вероятности и исправления ошибок [1].
На протяжении длительного времени многими учеными разрабатывались шкалы электроотрицательности (ЭО), экспериментальные и расчетные значения которых имели существенные отличия. Общего понимания того, что физически надо подразумевать под понятием ЭО, в рамках данной проблемы на настоящий момент не существует [2]. Тем не менее, по мнению многих ведущих ученых такое свойство атома как ЭО является одним из самых важных в химии. Это объясняется тем, что именно между значениями ЭО и иными значениями свойств атомов существует сильная взаимосвязь. Кроме того, само свойство — ЭО обуславливает поведение атомов при их взаимодействиях.
Находясь под влиянием результатов работы Шеннона, основные усилия были сосредоточены на получении математических зависимостей и максимально точных значений величин в последовательностях ЭО химических элементов, используя для этого приблизительно измеренные или рассчитанные в ходе эксперимента значения.
Тогда:
- Ненадежным в разной степени элементам в теории Шеннона можно сопоставить приблизительные экспериментальные данные ЭО атомов;
- Математическим аппаратам теории Шеннона (теории вероятности и исправления ошибок) — упорядоченное в соответствии с законом Д. И. Менделеева множество экспериментальных значений ЭО химических элементов и математический аппарат обработки результатов измерений;
- Надежной вычислительной системе Шеннона — выявленную математическую зависимость значений ЭО атомов в таблице Д. И. Менделеева.
Актуальность исследования заключается в том, что экспериментальные последовательности ЭО еще недостаточно хорошо изучены. В связи с этим такие исследования очень перспективны, так как полученные в результате их обработки математические зависимости могут содержать уточненные значения ЭО атомов и обладать необычными свойствами, способными предсказывать характер изменения других свойств и параметров атомов (например, радиус).
Цель исследования — это разработка математических выражений (формул), которые количественно описывают зависимости в последовательностях эмпирических величин ЭО и которые способны отобразить значения их ЭО на соответствующие им места в упорядоченном множестве химических элементов в таблицы Д. И. Менделеева.
Задачи исследования : изучение метрологических аспектов математической обработки результатов эксперимента;выявление математических закономерностей в изучаемой эмпирической последовательности ЭО атомов; вычисление уточненных значений ЭО и отображение полученных значений на соответствующие им места в упорядоченном множестве химических элементов в периодическом законе Д. И. Менделеева (таблице Д. И. Менделеева); анализ и обобщение полученных результатов и выдача рекомендаций на дальнейшие исследования.
Объект исследования

Предмет исследования — изучаемая в ходе исследования эмпирическая последовательность значений ЭО (свойств) химических элементов (атомов).
Гипотеза исследования — эмпирическая последовательность значений ЭО химических элементов содержит закономерности, которые при посредстве периодического закона Д. И. Менделеева и математического аппарата обработки результатов экспериментов могут быть выявлены и формализованы в виде математических формул.
В работе использовались методы: теоретического анализа и обобщения при изучении научной литературы; абстрагирования при выборе предмета исследования; методы наблюдения, сравнения и фиксирования наиболее значимых изменений предмета изучения; методы формализации и обобщения.
Теоретическая значимость настоящей работы состоит в том, что количественное описание периодического закона Д. И. Менделеева открывает в отношении химической систематики безграничные возможности [4].
- Состояние и перспективы развития Закона периодичности
1.1. Качественная и количественная стадии описания
Закона периодичности
Методические исследования, целью которых является привлечение внимания учащихся средней школы к актуальной научной проблеме — эволюции химических элементов закона Д. И. Менделеева, достаточно широко представлены в научно-популярной литературе [3; 4; 5; 6].
После открытия периодического закона «Менделеев поставил перед наукой ещё более грандиозную задачу: объяснить взаимную связь между всеми элементами, между их физическими и химическими свойствами» [3 с. 4].
Уже в 1913–1914 гг. И. Ридбергом была предложена математическая модель периодической системы. Он считал, что при таком моделировании совершенно естественным будет использование эмпирических численных значений характеристик и свойств химических элементов. Какой-либо гипотезы о природе самой материи, по его мнению, не требовалось [4].
Интерес ведущих ученых всего мира к математическому описанию структуры таблицы Д. И. Менделеева сохранился и до настоящего времени. В нашей стране данное направление науки возглавили такие ученые как И. С. Дмитриев и Д. Н. Трифонов. Разработанные ими теории позволили еще лучше понять природу атомов. Однако проблема построения математической модели таблицы еще далека от своего решения как в нашей стране, так и за рубежом [4; 5].
По глубокому убеждению Д. Н. Трифонова закон периодичности и периодическая система элементов раскрывают саму суть строения и свойства материи. Дальнейшее развитие данного направления, по его мнению, содержит две основные стадии — качественную и количественную.
Для качественной стадии характерно использование эмпирических значений, которые характеризуют только свойства атомов. На данной стадии причины периодичности не определяются [5; 6].
Количественная стадия рассматривается Д. Н. Трифоновым как процесс выявления функциональной зависимости (взаимозависимостей), содержащихся в последовательностях эмпирических значений свойств химических элементов. С этой целью применяются соответствующие разделы математики.
Анализ изложенного выше показал, что качественное описание характеризует лишь особенности изучаемых свойств и предшествует их количественному описанию, для создания которого могут быть тем или иным способом выявлены и отобраны наиболее подходящие математические зависимости [6].
1.2. Основные направления создания модели периодичности
Изучение научной литературы и информационных материалов в интернете было направлено на поиск исследований, связанных с определением количественных зависимостей в таблице Д. И. Менделеева. При этом, основное внимание было сосредоточено на отыскании зависимости вида:
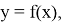
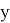
Часть ученых сходится во мнении, что свойства атомов не являются функцией их порядкового номера [5; 6]. Тем не менее, исследователи всего мира продолжают искать решение данной проблемы во многих различных направлениях. Первое базируется на дальнейшем развитии квантово-механических расчетов (какой-либо из физических моделей атома), второе использует теоретико-групповые подходы, посредством которых определяются закономерности в периодическом законе Д. И. Менделеева, в третьем применяется формально-математическое моделирование таблицы Д. И. Менделеева, содержащее приемлемую интерпретацию [4; 5; 6].
1.3. Научные методы, подходы и приемы, используемые Д. И. Менделеевым
Всестороннее изучение периодического закона Д. И. Менделеева невозможно себе представить без ознакомления с теми научными методами, подходами и приемами, которые использовал выдающийся исследователь. Наиболее полный анализ этих методов, был осуществлен Б. М. Кедровым в 1958 году [7]. К их числу относятся: методы индукции и дедукции, которыми Д. И. Менделеев временами пользовался одновременно, дополняя один метод другим; метод «восхождения», определяющий продвижение от низшего уровня познания к высшему; метод «обобщения», объединивший в себе варианты процедур и познавательных приемов обобщения; метод «сравнений», использующий процессы сопоставления объектов изучения и способствующий их систематизации [7].
Рассматривая перспективы развития химии как науки, Д. И. Менделеев по существу первым сформулировал проблему количественного описания открытого им периодического закона, определил, какие химические элементы должны находится в начале и в конце периода [7]. При предсказании еще неоткрытых элементов он использовал математический аппарат интерполяции [7].
Все разработанные Д. И. Менделеевым положения и факты, относящиеся непосредственно к периодическому закону, прошли проверку временем и приняты мировым научным сообществом. Их использование в рамках проводимой нами научно-исследовательской работы сочли оправданным.
1.4. Выбор математического аппарата для обработки эмпирических данных и установления зависимостей
Обработку изучаемых эмпирических последовательностей, как правило, осуществляют с помощью метода регрессионного анализа (или иначе метода наименьших квадратов). В нем заложена способность раскрывать аналитические зависимости между порядковыми номерами элементов (аргументом) и аппроксимирующей функцией по известным эмпирическим данным. При этом полагается, что наилучшей полученной аналитической зависимостью считается та, которая изначально основывается на особенностях изучаемого процесса. И самое главное: регрессионный метод способен учитывать взаимосвязь экспериментальных значений и тем самым осуществлять их сглаживание или «исправление» (выявлять зависимость) [8; 9].
Выбранные и используемые в работе варианты подбора аппроксимирующих функций, расчет их отклонений от последовательностей экспериментальных данных (точности) заимствованы из [9].
-
Исследование закономерностей изменения ЭО в
периодах таблицы
Д.
И.
Менделеева
- Закономерность в последовательности ЭО третьего периода
Следуя примеру Д. И. Менделеева, мы также приступили к исследованию таблицы с третьего периода, в котором великий ученый выделил и изучал простейшую «клеточку» — молекулу поваренной соли NaCl [7]. Этот период отличается от других монотонным возрастанием значений ЭО всех его атомов от Na до Cl включительно.
Для определения характера этих изменений был осуществлен предварительный расчет отношений значений ЭО последующего химического элемента к предыдущему с вычислением их среднего арифметического. Результат расчета представлен ниже:
(X(Mg):X(Na)+X(Al)X:(Mg)+X(Si):X(Al)+X(P):X(Si)+X(S):X(P)):5


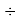

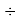

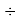

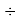

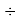
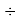






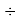


Полученные отношения мало отличаются между собой и практически равны среднему арифметическому.
Такой результат позволил выдвинуть гипотезу: последовательность значений ЭО в третьем периоде можно описать аналитической зависимостью, совпадающей с возрастающей геометрической прогрессией при величине знаменателя равным 1,2.
С целью подтверждения данной гипотезы была подобрана эмпирическая зависимость, которая позволила с высокой точностью рассчитать значения ЭО атома от его места положения в третьем периоде. Для этого был использован математический аппарат обработки эмпирических данных (регрессионный метод или метод наименьших квадратов), где в качестве аппроксимирующей была выбрана показательная функция.
Предварительно обработанные значения ЭО атомов из третьего периода таблицы Д. И. Менделеева приведены в таблице 1.
Таблица 1
Расчет значений аппроксимирующей функции для третьего периода
|
Элемент |
Na |
Mg |
Al |
Si |
P |
S |
|
Номер
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Табличная ЭО
|
1,01 |
1,23 |
1,47 |
1,74 |
2,1 |
2,6 |
|
Y
|
0,0095033 |
0,20701 |
0,38526 |
0,55388 |
0,74193 |
0,95551 |
|
Рассчитанная ЭО
|
1,0112455 |
1,217674 |
1,466242 |
1,765550 |
2,125958 |
2,559937 |
Расчет значений аппроксимирующей функции для третьего периода осуществляли с использованием приведенных ниже выражений:
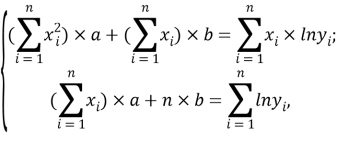
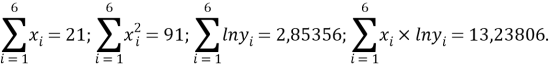
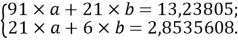
a

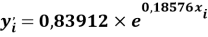
где знаменатель прогрессии равен: q

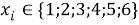
Для удобства дальнейшей работы с геометрическими прогрессиями их привели к следующему виду:
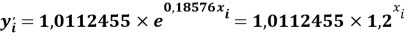
В отличии от представленного ранее выражения в последнем
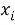
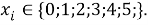
X(Na)
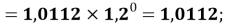
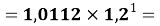
X(Al)
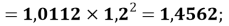

X(P)
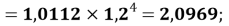
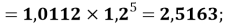
X(Cl)
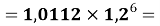
Для сопоставления рассчитанных значений ЭО Na по периоду и по группе определили аппроксимирующую функцию для всей первой группы таблицы.
Предварительно обработанные значения ЭО атомов из первой группы таблицы Д. И. Менделеева приведены в таблице 2.
Таблица 2
Расчет значений аппроксимирующей функции для первой группы
|
Элемент |
Cs |
Rb |
K |
- |
- |
Li |
- |
Na |
|
Номер
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Табличная ЭО
|
0,86 |
0,89 |
0,91 |
- |
- |
0,975 |
- |
1,01 |
|
Y
|
-0,151 |
-0,117 |
-0,094 |
- |
- |
- |
- |
- |
|
Рассчитанная ЭО
|
0,8617 |
0,8864 |
0,9118 |
- |
- |
0,9925 * |
1,0209 * |
1,0502 * |
*получены путем экстраполяции.
Расчет значений аппроксимирующей функции для первой группы осуществляли с использованием приведенных ниже выражений:

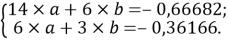
a
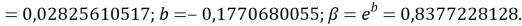
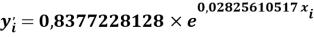
где знаменатель прогрессии равен:
q
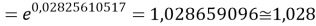
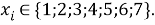
Учитывая, что значения знаменателя прогрессии и рассчитанное значение ЭО Na практически различаются на 0,04 (см. таблицы 1 и 2, их среднее арифметическое равно 1.03), выразили аппроксимирующую функцию через значение знаменателя прогрессии:
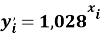
и приняли позицию ЭО X(Na) за начало отсчета. При этом:
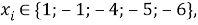
X(Na)
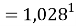
X(Li)
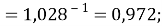
X(K)
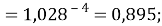
X(Rb)
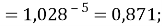
X(Cs)
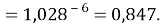
Сравнивая рассчитанные значения ЭО Na по периоду и по группе установили их отличие. Для определения «правильного» значения ЭО Na дополнительно произвели оценку погрешностей для аппроксимирующей функции при значениях ЭО натрия X(Na) равных 1,01, 1,02, 1,03 и 1,025.
Выбор более «правильного» значения ЭО осуществляли путем определения минимальной среднеквадратичной погрешности всей совокупности химических элементов в периоде за исключением ЭО хлора Cl (ЭО хлора существенно отличается в экспериментах Полинга и Оллреда и Рохова).
При значении ЭО натрия X(Na)=1,01 среднее квадратичное отклонение составило
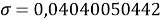
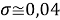
Таблица 3
Расчет среднего квадратичного отклонения для третьего периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
Na |
1,01 |
1,01 |
0,0 |
0,0 |
|
Mg |
1,23 |
1,212 |
0,018 |
0,000324 |
|
Al |
1,47 |
1,4544 |
0,0156 |
0,00024336 |
|
Si |
1.74 |
1,74528 |
0,00528 |
0,0000278784 |
|
P |
2,1 |
2,094336 |
0,005664 |
0,000032080896 |
|
S |
2,6 |
2,5132032 |
0,0867968 |
0,00753368449 |
При значении ЭО натрия X(Na)=1,02 среднее квадратичное отклонение составило
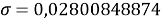
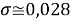
Таблица 4
Расчет среднего квадратичного отклонения для третьего периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
Na |
1,01 |
1,02 |
0,01 |
0,0001 |
|
Mg |
1,23 |
1,224 |
0,006 |
0,000036 |
|
Al |
1,47 |
1,4688 |
0,0012 |
0,0000144 |
|
Si |
1.74 |
1,76256 |
0,02256 |
0,0005089536 |
|
P |
2,1 |
2,115072 |
0,015072 |
0,000227165184 |
|
S |
2,6 |
2,5380864 |
0,0619136 |
0,003833293865 |
При значении ЭО натрия X(Na)=1,03 среднее квадратичное отклонение составило
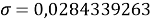
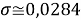
Таблица 5
Расчет среднего квадратичного отклонения для третьего периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
Na |
1,01 |
1,03 |
0,02 |
0,0004 |
|
Mg |
1,23 |
1,236 |
0,006 |
0,000036 |
|
Al |
1,47 |
1,4832 |
0,0132 |
0,00017424 |
|
Si |
1.74 |
1,77984 |
0,03984 |
0,0015872256 |
|
P |
2,1 |
2,135808 |
0,035808 |
0,001282212864 |
|
S |
2,6 |
2,5629696 |
0,0370304 |
0,001371250524 |
При значении ЭО натрия X(Na)=1,025 среднее квадратичное отклонение составило
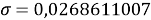
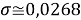
Таблица 6
Расчет среднего квадратичного отклонения для третьего периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
Na |
1,01 |
1,025 |
0,015 |
0,000225 |
|
Mg |
1,23 |
1,23 |
0,00 |
0,00 |
|
Al |
1,47 |
1,476 |
0,006 |
0,000036 |
|
Si |
1.74 |
1,7712 |
0,0312 |
0,00097344 |
|
P |
2,1 |
2,12544 |
0,02544 |
0,0006471936 |
|
S |
2,6 |
2,550528 |
0,049472 |
0,002447478784 |
Расчеты показали, что более «правильное» значение ЭО натрия равно X(Na)=1,025 при среднеквадратичном отклонении
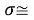
Следовательно, с позиций метрологии погрешность данных в таблице А.ښОллреда и Ю. Рохова составляет
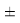
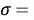

Изложенное выше позволяет считать, что значения ЭО химических элементов третьего периода образуют геометрическую прогрессию, так как «Правильность — степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или в отсутствии эталона измеряемой величины — степень близости среднего значения, полученного на основании серии результатов измерений, к принятому опорному значению» [11; 12; 13].
Приведенные выше результаты исследования подтверждают правильность выдвинутой гипотезы о том, что последовательность значений ЭО в третьем периоде правомерно описать аналитической функцией, совпадающей с возрастающей геометрической прогрессией при величине знаменателя равным 1,2.
Так как окончательное значение ЭО Na было выбрано равным 1,025, то приняли ему равным и знаменатель геометрической прогрессии для ЭО химических элементов в первой группе:
X(Na)
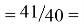
X(Li)
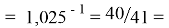
X(K)
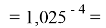
X(Rb)
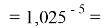
X(Cs)

Рассчитанные значения ЭО отличаются от приводимых в таблице не более, чем на 0,006.
Таким образом, ЭО элементов третьего периода имеют значения, совпадающие с геометрической прогрессией со знаменателем
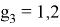
X(Na)

X(Mg)





X(Al)





X(Si)





X(P)





X(S)




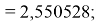
X(Cl)





X(Ar)

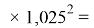
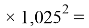
2.2. Закономерности в последовательностях ЭО четвертого, пятого и шестого периодов
При расчетах p-элементов четвертого, пятого и шестого периодов также была выдвинута гипотеза, что характер изменения ЭО атомов соответствует закону геометрической прогрессии . Первыми (опорными) членами этих прогрессий считали ЭО Ga, In и Tl.
Таблица 7
Расчет среднего квадратичного отклонения для четвертого периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
Ga |
1,82 |
1,81 |
0,01 |
0,0001 |
|
Ge |
2,02 |
2,0091 |
0,0109 |
0,00011881 |
|
As |
2,2 |
2,230101 |
0,030101 |
0,00090607020 |
|
Se |
2,48 |
2,47541211 |
0,00458789 |
0,00002104836 |
|
Br |
2,74 |
2,747707442 |
0,007707442 |
0,00005940466 |
Среднее квадратичное отклонение с учетом значащих цифр:
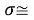
Таблица 8
Расчет среднего квадратичного отклонения для пятого периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
In |
1,49 |
1,47 |
0,02 |
0,0004 |
|
Sn |
1,72 |
1,6317 |
0,0883 |
0,00779689 |
|
Sb |
1,82 |
1,811187 |
0,0008813 |
0,0000007766 |
|
Te |
2,01 |
2,01041757 |
0,00041757 |
0,0000001743 |
|
I |
2,21 |
2,231563503 |
0,0215635027 |
0,0004649846 |
Среднее квадратичное отклонение (без включения в расчет значения ЭО олова Sn) с учетом значащих цифр:
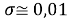
Таблица 9
Расчет среднего квадратичного отклонения для шестого периода
|
Химический элемент |
Табличные значения |
Расчетные значения |
Разность значений |
Квадрат разности |
|
Tl |
1,44 |
1,44 |
0,0 |
0,0 |
|
Pb |
1,55 |
1,5552 |
0,0052 |
0,000002704 |
|
Bi |
1,67 |
1,679616 |
0,009616 |
0,00000925251 |
|
Po |
1,76 |
1,81398528 |
0,05398528 |
0,00029144104 |
|
At |
1,96 |
1,959104102 |
0,0008958976 |
0.0000000802 |
Среднее квадратичное отклонение с учетом значащих цифр:
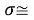
Опорные (первые) значения ЭО p-элементов для каждого из периодов не обязаны совпадать с представленными в таблице. Их значения выбирали с учетом минимального среднего квадратичного отклонения значений всех остальных ЭО p-элементов.
Результаты расчетов показали, что минимальное среднее квадратичное отклонение (погрешность) экспериментальных данных от значений для геометрической прогрессии во всех расчетах не превышает значений
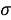
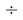
1,08=36



1,17=39



Использовались и другие коэффициенты, которые не кратны 0,03.
Величины ЭО щелочноземельных металлов в четвертом, пятом и шестом периодах определили с помощью выражений, в которых использовались коэффициенты равные 1,14 ; 1,11:
X(Ca)


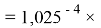

X(Sr)


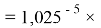

X(Ba)




При проведения сквозных расчетов ЭО в четвертом, пятом и шестом периодах использовались коэффициенты равные 1,11; 1,11; 1,14; 1,4836; 1,50447 и 1,75255 . (В связи с этим, рассчитанные ЭО незначительно отличаются от тех, которые ранее были приведены в таблицах 7, 8 и 9).
В четвертом и пятом периодах p-элементы имеют знаменатели геометрической прогрессии равные

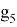
X(Ga)



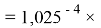


X(Ge)





X(As)





X(Se)





X(Br)





X(Kr)


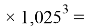
X(In)



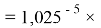


X(Sn)





X(Sb)





X(Te)





X(I)





X(Xe)


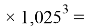
Для шестого периода, который содержит еще и f–элементы, знаменатель геометрической прогрессии для p-элементов равен
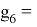
X(Tl)






X(Pb)





X(Bi)





X(Po)





X(At)





X(Rn)

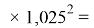
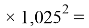
Сравнение рассчитанных значений ЭО с приведенными в таблице показало, что, кроме двух (для X(Sn) и X(Po)), все остальные значения ЭО отличаются от табличных не более чем на
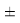
2.3. Закономерность в последовательности ЭО второго периода
Для нахождения аппроксимирующей функции второго периода была использована часть предложенных ранее рабочих коэффициентов: 1,14; 1,17; 1,2 и 1,23. Все они делятся на 3, взаимно просты и представляют собой последовательные члены участка арифметической прогрессии с разностью равной 0,03.
Принимая значение ЭО фтора равным по Оллреду и Рохову 4,1 и деля его последовательно два раза на 1,17 и по одному разу на 1,2 и 1,23 получили последовательность значений, совпадающую со значениями ЭО фтора F, кислорода O, азота N, углерода C и бора B:
4,1:1,17=3,5043; 3,5043:1,17=2,9951; 2,9951:1,2=2,4959; 2,4959:1,23=2,0292.
Принимая значение ЭО фтора равным по Полингу равным 4,0 и деля его последовательно на 1,14; 1,17; 1,2 и 1,23 также получили последовательность значений, совпадающую со значениями ЭО фтора F, кислорода O, азота N, углерода C и бора B:
4,0:1,14=3,5087; 3,5087:1,17=2,9989; 2,9989:1,2=2,4991; 2,4991:1,23=2,0318.
Так как большинство исследователей придерживается значения ЭО фтора равным 4,0, то была выбрана в качестве рабочей последовательность коэффициентов: 1,14; 1,17; 1,2 и 1,23.
Данные коэффициенты взаимно просты. Их разложение на простые множители представлено ниже:

Фрагмент этой арифметической прогрессии представим и в виде:
1,14








ЭТО ИНТЕРЕСНО!!!
Отношение коэффициентов, стоящих по обе стороны от углерода
C
, равно 1,23
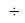

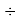

Значения ЭО элементов второго периода получены из элементов арифметической прогрессии, взаимно простого с ними числа 1,0598537
(10598537 — простое число) и числа 1,025:
X(Li)

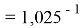
X(Be)





X(B)







X(C)



X(N)
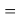


X(O)



X(F)



X(Ne)


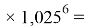
Элементы второго периода в своей основе содержат члены арифметической прогрессии: 1,14; 1,17; 1,2 и 1,23, число 1,0598537. Рассчитанные по ним значения ЭО отличаются от приводимых в таблице не более чем на
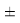
Анализ проведенных выше исследований позволил выдвинуть гипотезу: текущее значение ЭО атома равно произведению принадлежащего только ему коэффициента на предыдущие значения коэффициентов ЭО атомов и первого в периоде значения ЭО. Или иначе, в любом периоде существует только одна операция — умножение!
2.3. Закономерность в последовательности ЭО первого периода
Значения ЭО элементов первого периода также были получены из элементов арифметической прогрессии, взаимно простых с ними чисел 1,0598537, 1,0391677 (10598537 и 10391677 — простые числа) и числа 1,025:
X(H)
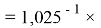






X(He)



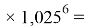
Используя приближенные значения чисел 1,0598537


Значение ЭО для водорода X(H) получено из ЭО для X(B) умножением на коэффициент 1,0391677:
X(H)
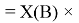

Элементы первого периода в своей основе содержат, также как и во втором периоде, члены арифметической прогрессии: 1,14; 1,17; 1,2 и 1,23, число 1,0598537 и дополнительно число 1,0391677. Рассчитанные по ним значения ЭО отличаются от приводимых в таблице не более чем на
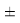
2.4. Закономерности в последовательностях ЭО d -элементов в четвертом, пятом и шестом периодах
Для нахождения аппроксимирующей функцииd-элементов четвертого периода использовались члены арифметической прогрессии: 1,11; 1,095; 1,08; 1,065; 1,05; 1,035; 1,02; 1,005; 0,99 с разностью 0,015. Для пятого периода также использовались члены арифметической прогрессии: 1,11; 1,0: 1,08; 1,065; 1,05; 1,035 с разностью 0,015. Вместо коэффициента 1,095 использовался коэффициент равный 1,00 из-за перескока электронов. Для шестого периода использовались члены арифметической прогрессии: 1,125; 1,095; 1,065; 1,035 с разностью 0,03.
Значения ЭО d-элементов четвертого периода рассчитывались следующим образом:
X(Sc)

X(Ti)



X(V)




X(Cr)
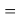



X(Mn)




X(Fe)




X(Co)




X(Ni)




X(Cu)




X(Zn)




Здесь 0,991 — поправочный коэффициент.
Значения ЭО d-элементов пятого периода рассчитывались следующим образом:
X(Y)

X(Zr)




X(Nb)



X(Mo)
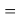



X(Tc)




X(Ru)




X(Rh)




X(Pd)

X(Ag)

X(Cd)

Здесь 0,991 –поправочный коэффициент.
Значения ЭО d-элементов шестого периода рассчитывались следующим образом:
X(La)

X(Hf)



X(Ta)



X(W)
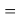


X(Re)



X(Os)



X(Ir)



X(Pt)

X(Au)

X(Hg)

Сравнение рассчитанных значений ЭО d-элементов четвертого, пятого и шестого периодов со значениями ЭО, приведенными в таблице, показало, что, кроме трех элементов, все остальные двадцать семь значений ЭО отличаются от табличных не более чем на

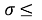
Данная гипотеза оказалась справедливой при вычислении ЭО в любом периоде таблицы.
2.5. Расчет электроотрицательности инертных газов
Отдельно были рассмотрены благородные газы, которые представляют самостоятельную группу химических элементов в таблице Д. И. Менделеева. Особенность расчета их ЭО состоит в том, что используемые коэффициенты равны
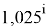
Наличие коэффициента
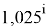
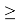
ЭО благородных газов рассчитывалась по схеме:
X(He)



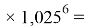
X(Ne)


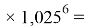
X(Ar)

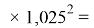
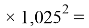
X(Kr)


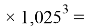
X(Xe)


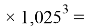
X(Rn)

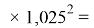
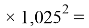
2.6. Оценка точности расчета ЭО атомов
А. Оллред и Ю. Рохов для приведения полученных ими данных в соответствие с данными шкалы Л. Полинга подобрали эмпирическое математическое выражение [13], которое в ряде случаев оказалось точнее:
X(i)

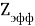
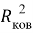
Даже при высокой точности вычисления значения эффективного заряда ядра атома результирующая точность расчета ЭО по приведенному выражению не может быть больше чем точность численного значения ковалентного радиуса. Именно поэтому А. Оллред и Ю. Рохов ограничили значения ЭО атомов в таблице вторым знаком после запятой.
Вместе с тем, в науке и технике существуют договоренности, которые, «когда погрешность числа не указана, то следует считать, что абсолютная погрешность его равна половине единицы разряда последней цифры» [10, с. 125] и «в числах, взятых из таблиц, содержатся только верные цифры, и погрешности их не превышают половины разряда последней цифры» [10, с. 127]. Следовательно, с позиций метрологии погрешность данных в таблице А. Оллреда и Ю. Рохова составляет
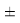

Анализ результатов расчетов, приведенных в таблицах, позволил считать, что А. Оллред и Ю. Рохов в своих вычислениях для «сглаживания» результатов расчета ЭО применяли регрессионный анализ или метод наименьших квадратов. Тем не менее, они не подбирали значения опорных ЭО p-элементов в периодах (в [9] это точка

Проведенные нами дополнительные вычисления позволили получить более точные результаты, скорректировав значения ЭО атомов в таблице на
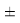
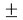
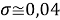
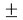

2.7. Формулы для расчета ЭО pd-элементов таблицы
Формула для вычисления ЭО sp-элементов третьего периода:
X(Na
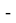
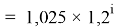
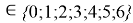
X(Na)



Формула для вычисления ЭО p-элементов второго периода:
X(B
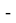


i
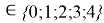
X(B)



В данной формуле коэффициенты представлены в виде: 1,23








Формула для вычисления ЭО p-элементов четвертого периода:
X(Ga
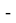

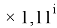
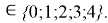
X(Ga)



Формула для вычисления ЭО p-элементов пятого периода:
X(I
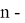

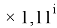
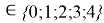
X(In)



Формула для вычисления ЭО p-элементов шестого периода:
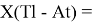
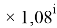
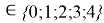
X(Tl)



Формула для вычисления ЭО d-элементов четвертого периода:


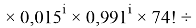
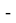
i
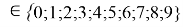
X(Sc)



В данной формуле коэффициенты представлены в виде:
1,11








1,05








Формула для вычисления ЭО d-элементов пятого периода:

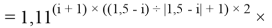
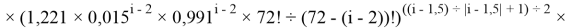

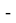

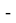
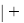
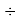

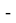

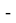
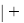
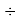


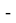

где i
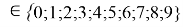
X(Y)



В данной формуле коэффициенты представлены в виде: 1,11










Карманный калькулятор факториалы более 69! не вычисляет!!!
Формула для вычисления ЭО d-элементов шестого периода:
X(i)
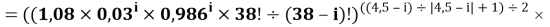
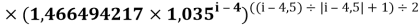

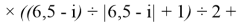
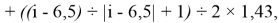
где i
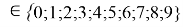
X(La)



В данной формуле коэффициенты представлены в виде:
1,125
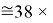

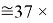


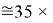

Это интересно. Изменения ЭО в последовательности d-элементов в шестом периоде рассчитываются по двум разным формулам.
Ниже приведены формулы расчета ЭО атомов с привязкой по месту их положения в таблице Д. И. Менделеева. Отличие этих формул от приведенных выше состоит в том, что для каждой группы химических элементов приводится свой показатель степени (переключатель) принимающий значения 0 или 1. Все формулы последовательно перемножаются. В вычислениях участвует только та формула, показатель степени которой равен 1 в зависимости от значения i. Все остальные формулы будут иметь значение равное 1 при показателе степени равном 0.
Общая формула имеет вид:
X(i)

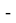

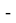

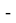

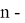
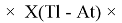
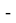

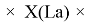
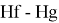
X(B
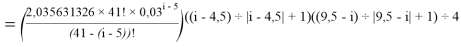
X(Na

X(Ga

X(I

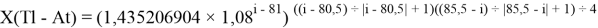
В с вязи с громоздкостью формы записи переключателя, формулы для d-элементов не представлены.
- Заключение
Материалом для проведенного нами исследования послужили труды выдающихся ученых. К их числу относятся Д. И. Менделеев, Л. Полинг, А. Оллред, Ю. Рохов, Б. М. Кедров, Д. Н. Трифонов, И. С. Дмитриев и другие. Всесторонний анализ их трудов позволил сделать следующие выводы:
В связи с большой трудоемкостью квантово-механических расчетов, недостаточной проработкой теоретико-групповых подходов и несовершенством формального математического моделирования проблема количественного описания периодического закона Д. И. Менделеева еще не решена. Ее решение открывает неограниченные возможности в отношении химической систематики и химии в целом.
Научные методы, подходы и приемы, которыми пользовался в своей деятельности Д. И. Менделеев, значимы и в настоящее время. Их применение в качестве инструмента исследования гарантирует успех в науке.
Регрессионный метод обработки экспериментальных данных является одним из самых давних. Тем не менее, он является очень плодотворным, так как позволяет не только выявлять математические зависимости в эмпирических последовательностях, но и осуществлять их сглаживание или «исправление» с приемлемой точностью.
По результатам проведенного исследования можно сделать следующие выводы:
Цель исследования достигнута. Гипотеза подтверждена. Впервые выявлены закономерности, на основании которых «выведены» математические формулы для spd-элементов, позволяющие количественно описывать зависимости в последовательностях эмпирических величин ЭО и способные отображать значения их ЭО на соответствующие им места в упорядоченном множестве химических элементов в таблице Д. И. Менделеева.
Выявлена взаимосвязь ЭО третьего периода и первой группы таблицы Д. И. Менделеева. Обе последовательности значений ЭО элементов совпадают с геометрическими прогрессиями. Значение знаменателя первой группы совпадает с ЭО X(Na). Данный феномен свидетельствует о наличии взаимосвязи значений ЭО атомов во всех периодах таблицы.
Все выявленные математические формулы в своем составе содержат специально подобранные коэффициенты 1,14; 1,17; 1,2 и 1,23. В формулах для расчета ЭО p-элементов в качестве знаменателя геометрической прогрессии использовался какой-либо один из этих коэффициентов.
В формулах для расчета ЭО p-элементов второго периода и d-элементов использовались упорядоченные наборы коэффициентов в виде фрагментов убывающих арифметических прогрессий.
Установлено, что каждое текущее значение ЭО атома равно произведению принадлежащего только ему значению коэффициента на предыдущие значения коэффициентов ЭО атомов и первого значения ЭО в периоде. В связи с этим, в любом периоде для вычисления ЭО химического элемента существует только одна операция — умножение!
Получены более точные значения ЭО атомов. В связи с отсутствием истинных (эталонных) значений ЭО оценить полученную в данной работе точность не представляется возможным. Однако, можно утверждать, что отклонение рассчитанных значений ЭО от приводимых в таблице уменьшилось с
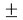
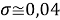
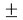
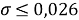
Остались невыявленными аналитические зависимости для щелочноземельных элементов, лантанидов, актинидов и благородных газов. В данном направлении исследование может быть продолжено.
Полученные формулы и зависимости «не претендуют на обобщение, но они подчеркивают удивительную гармоничность структуры периодической системы» [4, стр. 145]. Вместе с тем, в данной работе исследованы существенные фрагменты периодической системы и поэтому «можно говорить о количественной интерпретации периодической системы на основе чисто математических представлений» [4, стр.146].
Литература:
- Шеннон К. Э. Работы по теории информации и кибернетике. — М.: Издательство иностранной литературы, 1963. — 829 с.
- Еремин В. В., Борщевский А. Я. Основы общей и физической химии: Учебное пособие. Долгопрудный: Издательский Дом
- «Интеллект», 2018. — 848 с.
- Петрянов И. В., Трифонов Д. Н. Великий закон. — М.: Педагогика, 1984. — 128 с.
- Кораблева Т. П., Корольков Д. В. Теория периодической системы: Учебное пособие. — СПб.: Издательство С.-Петербургского университета, 2005.- 174 с.
- Дроздов О. М., Жохов А. Л., Томилина Л. И., Ведущая роль прикладной математики в совершенствовании курса химии средней школы на современном этапе. Издательский дом. — Кривой Рог — 2010. 300с.
- Глава 7 проблема математизации периодического закона. [Электронный ресурс] URL: https://uchebilka.ru/matematika/2315/index.html?page=39 Загл. с экрана.
- Кедров Б. М. День одного великого открытия, издательство Социально-экономической литературы, М, 1958. -560с.
- Румшиский Л. З. Математическая обработка результатов эксперимента. М., Наука, 1971, 192 с.
- Коломиец Л. В., Поникарова Н. Ю. Метод наименьших квадратов: методические указания — Самара., Издательство Самарского университета, 2017. — 32 с.
- Кондрашов А. П., Шестопалов Е. В. Основы физического эксперимента и математическая обработка результатов измерений. Учебник для техникумов. М., Атомиздат, 1977, 200 с.
- Мнимая точность [Электронный ресурс] URL:
- https://ru.wikipedia.org/wiki/. Загл. с экрана.
- Точность [Электронный ресурс] URL: https://ru.wikipedia.org/wiki/. Загл. с экрана.
- Черкасов А. Р., Галкин В. И., Зуева Е. М., Черкасов Р. А. Успехи химии, 67 (5) (1998). С. 423–441.