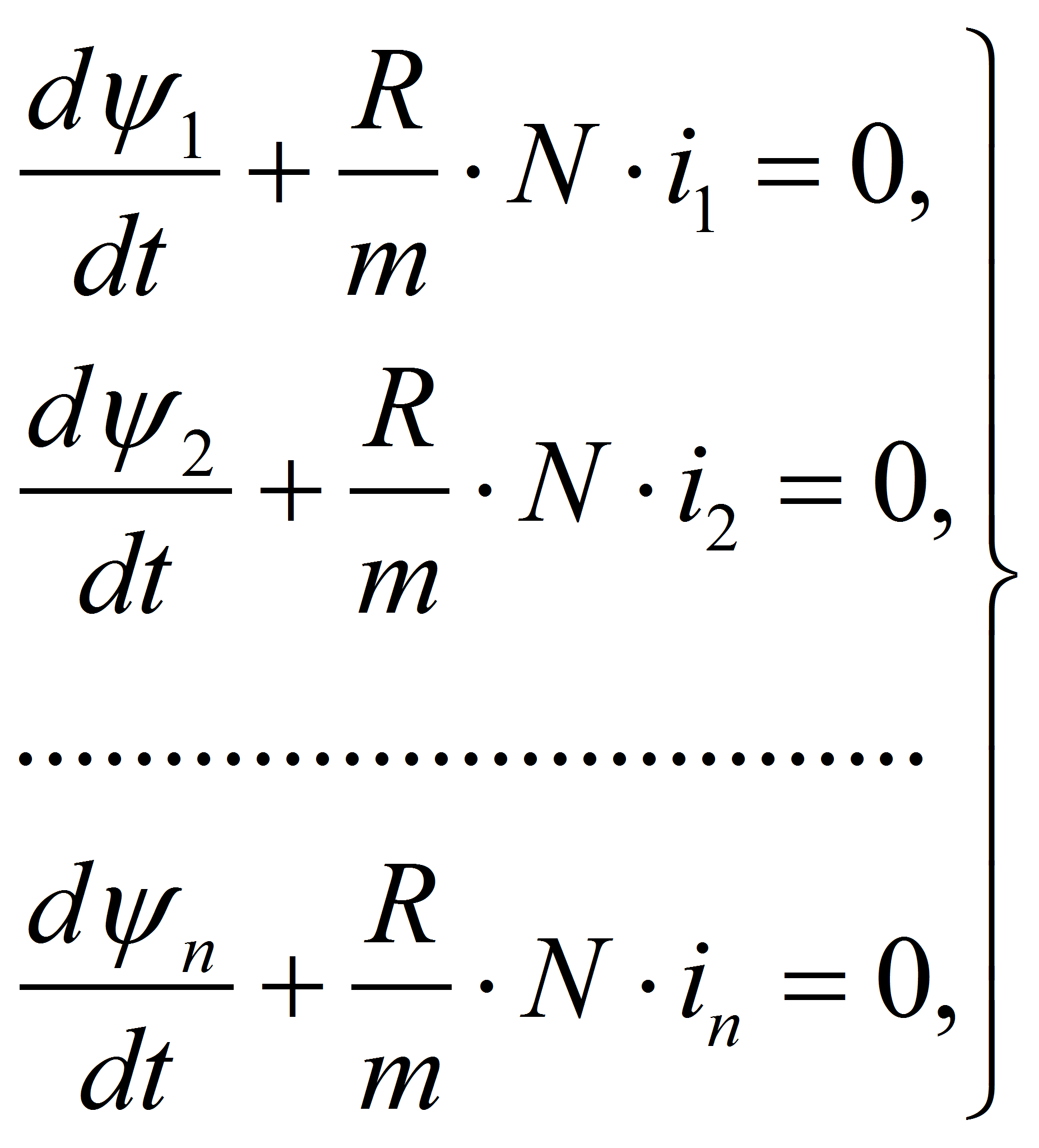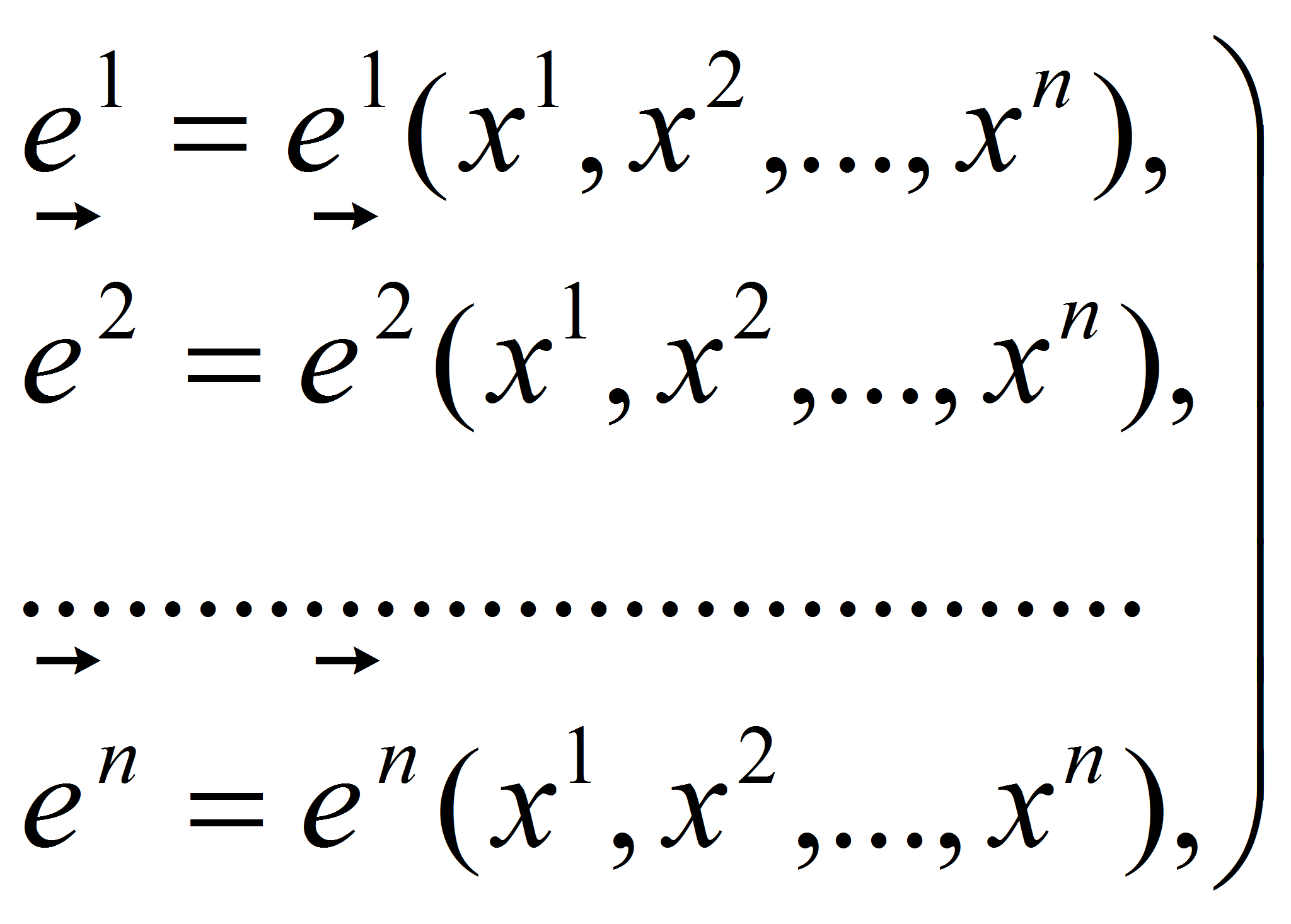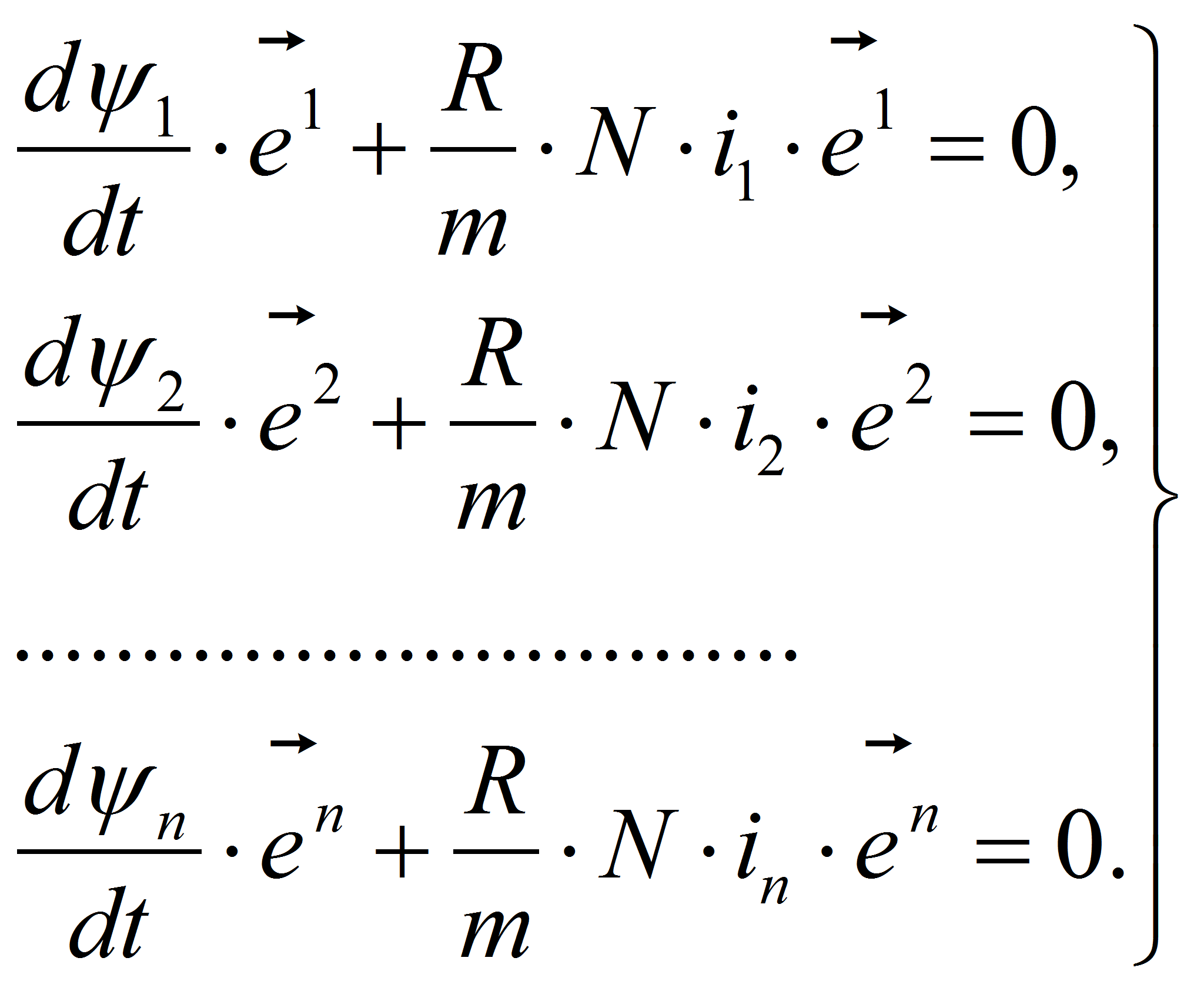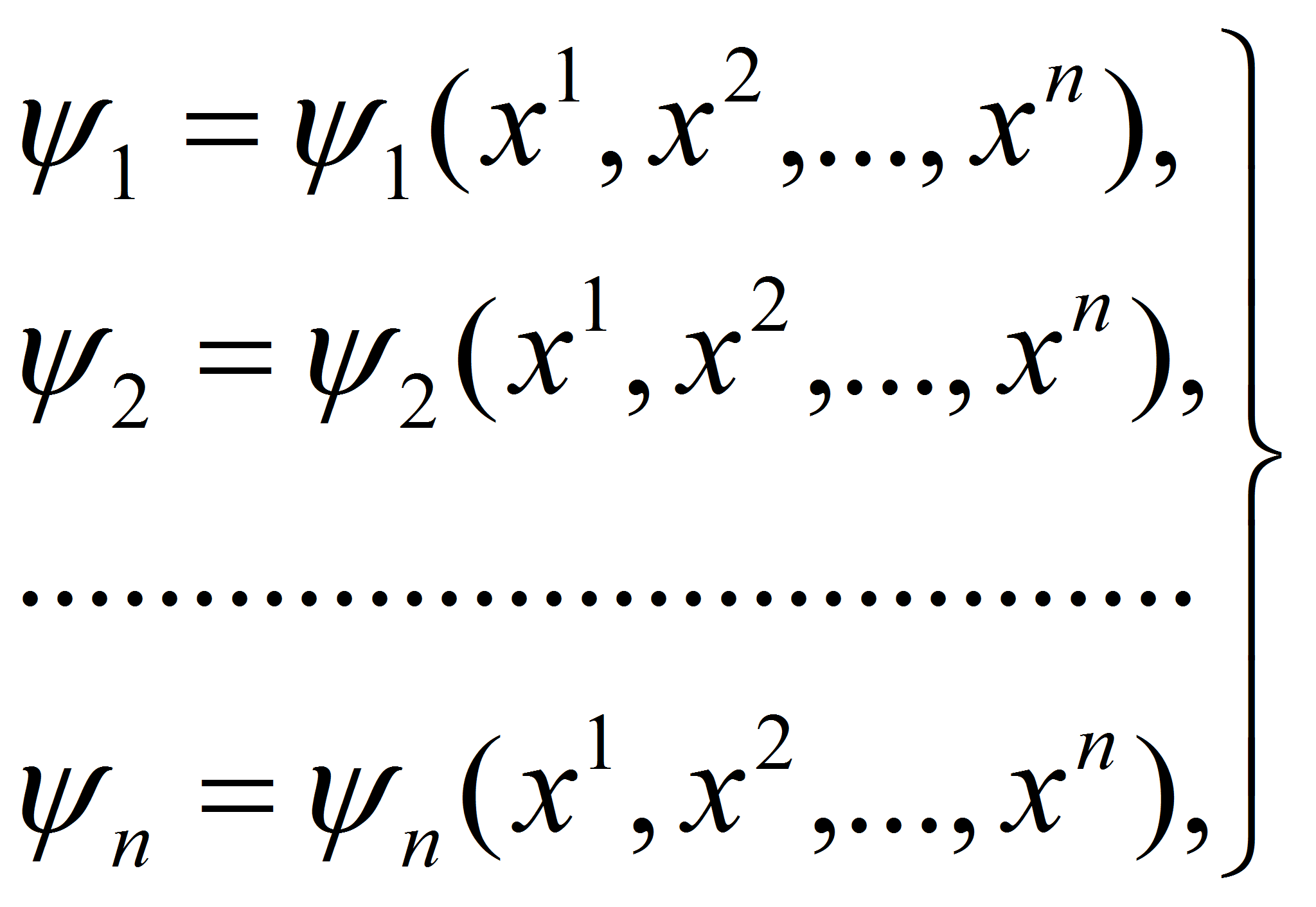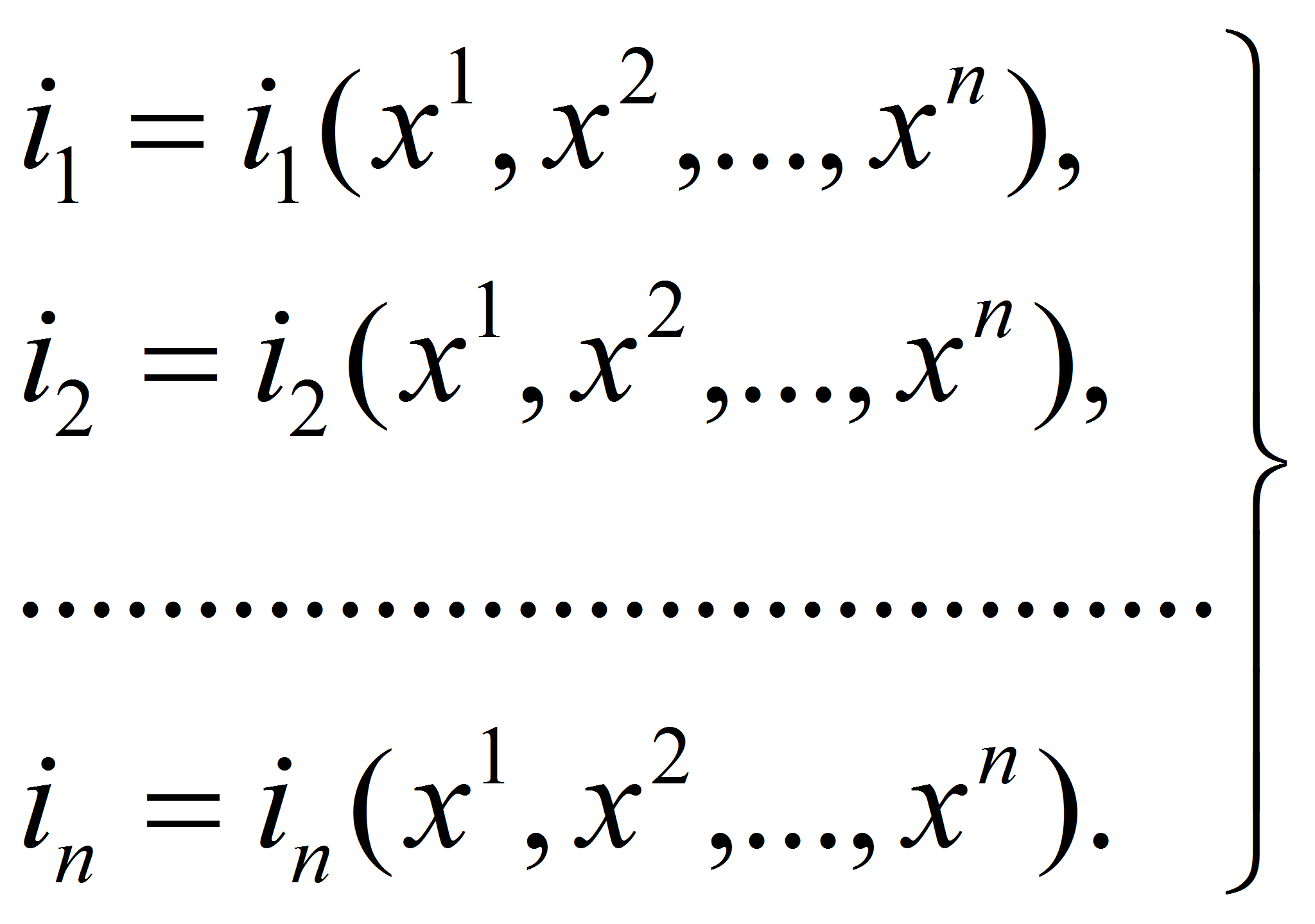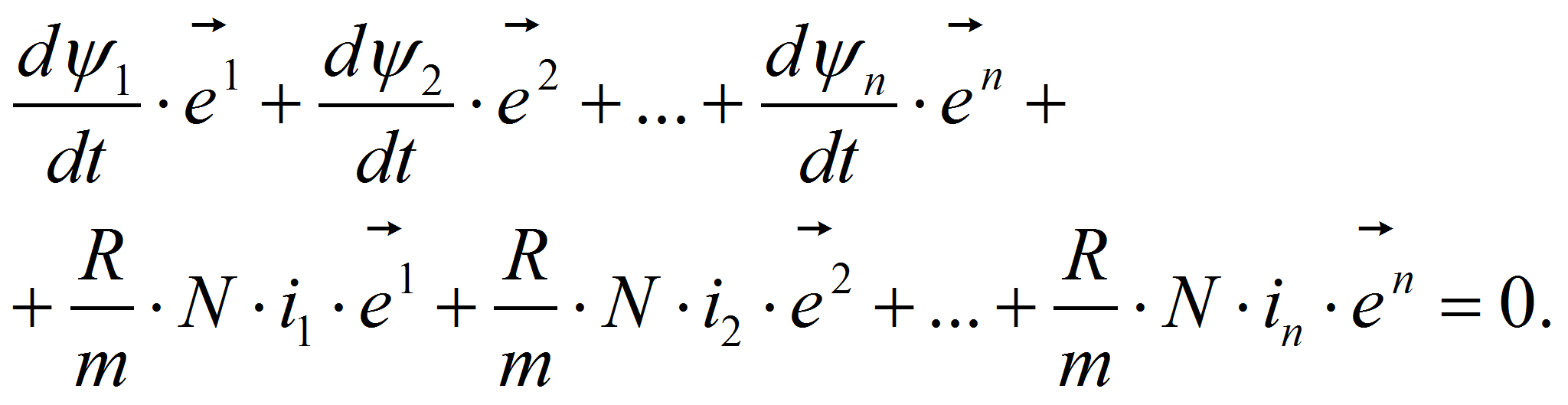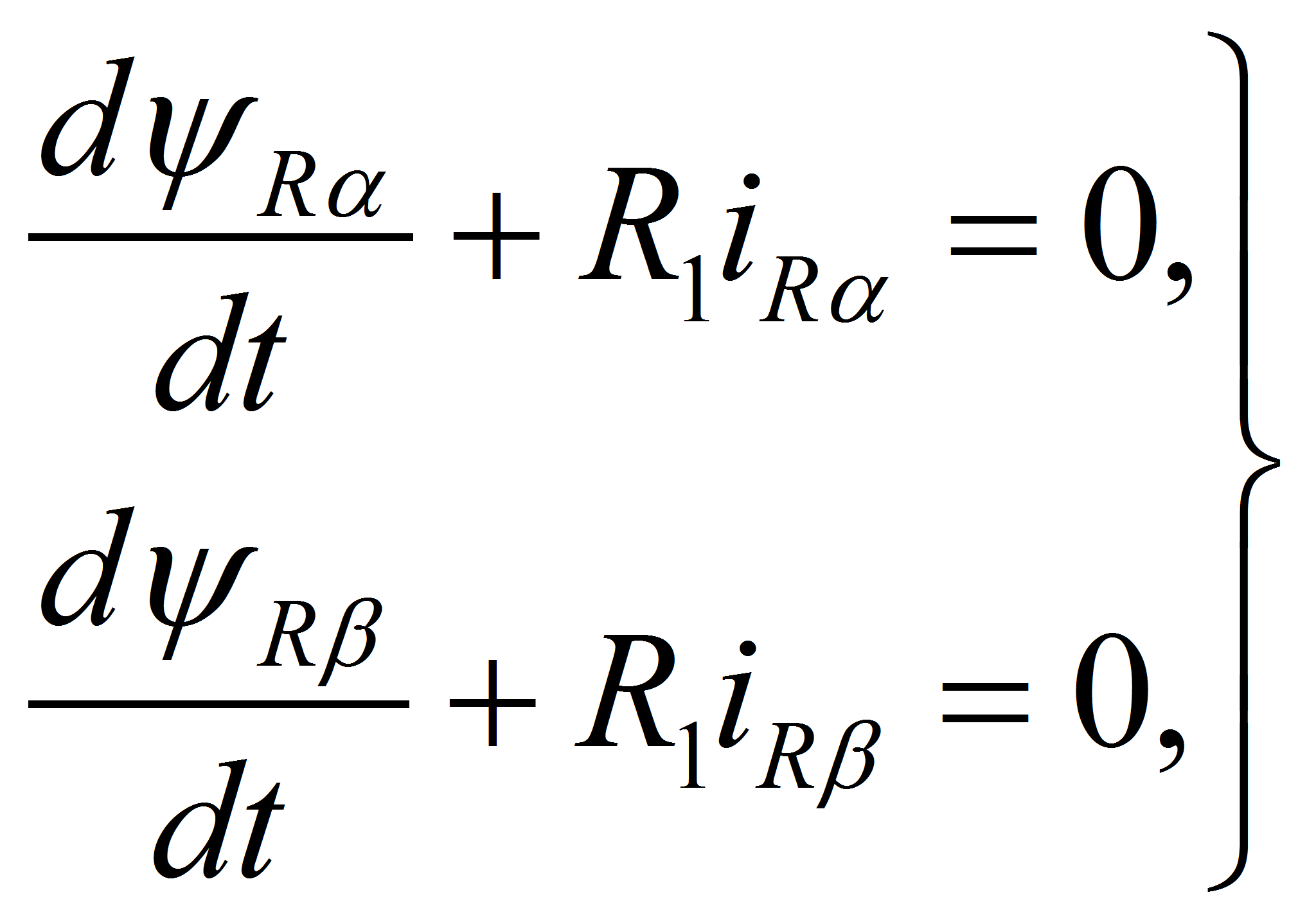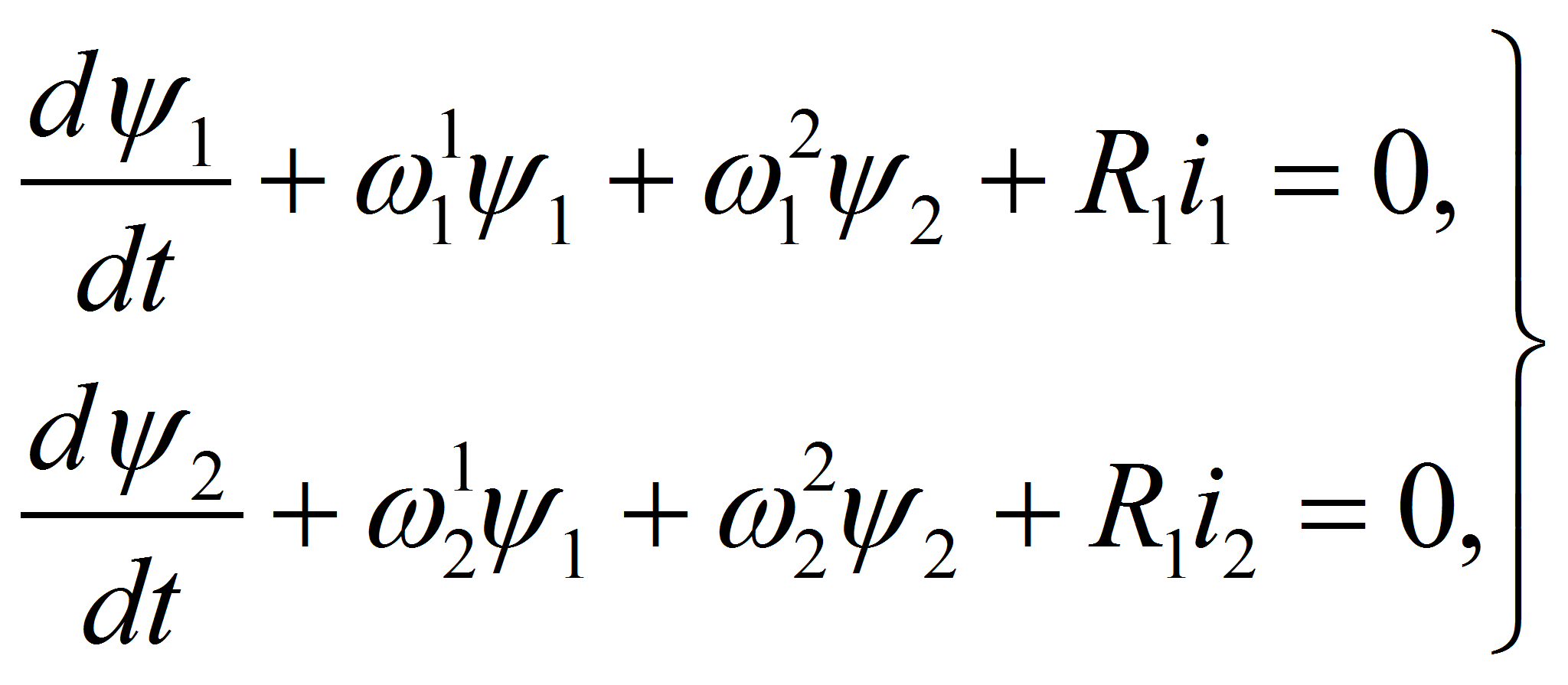В процессе работы короткозамкнутого асинхронного двигателя (АД) скольжение может изменяться. При скольжении, не равном нулю, в большей или меньшей степени возникает эффект вытеснения тока в стержнях ротора. В электротехнике расчет этого эффекта осуществляют путём введения на переменном токе понятия "эффективное сечение". Это понятие предполагает, что эквивалентное активное сопротивление стержней увеличивается с повышением частоты тока ротора. Однако увеличение эквивалентного активного сопротивления это не единственное проявление эффекта вытеснения тока. Важнее то обстоятельство, что фаза вектора плотности тока перераспределяется по сечению стержней в зависимости от частоты. Поэтому динамические математические модели АД, не учитывающие перераспределение фазы вектора плотности тока, могут в расчётах привести (и приводят) к значительным ошибкам. Кроме того, такие модели, положенные в основу построения систем управления, наблюдателей, идентификаторов состояния и параметров, ограничивают диапазон регулирования скорости асинхронных электроприводов.
В данной статье поставлена задача более детального математического описания эффекта вытеснения тока в стержнях ротора короткозамкнутого (АД) с учётом перераспределения вектора плотности тока по сечению стержней ротора. Решение поставленной задачи достигнуто на основе тензорного анализа электромагнитных процессов в рамках теории электрических цепей с сосредоточенными параметрами.
Пусть активное сопротивление каждого стержня, измеренное
на постоянном токе (по закону Ома), равно
,
а число стержней в роторе
.
Тогда эквивалентное сопротивление всех
стержней, включенных параллельно в короткозамкнутом роторе, на
постоянном токе будет равно
.
Мысленно разделим сечение каждого стержня на большое
число (
)
тонких проводников. Пусть (для упрощения анализа) активное
сопротивление всех тонких проводников будет одинаковым. Тогда
активное сопротивление каждого тонкого проводника на постоянном токе
будет равно
.
При достаточно большом значении
эффектом вытеснения тока в тонких проводниках можно пренебречь. Но,
что важно, в тонких проводниках не только сила тока, но и фаза
вектора плотности тока будут различаться.
Электромагнитные процесы в роторе могут быть представлены теперь (с учётом разбиения стержней ротора на тонкие проводники) следующей системой высокого порядка однотипных уравнений:
(1)
где
общее число тонких проводников во всех стержнях ротора,
потокосцепления тонких проводников;
сила тока в тонких проводниках. В (1) сопротивление тонких
проводников, равное
,
может зависеть от материала, температуры, площади сечения (от
),
но, главное, это сопротивление не будет зависеть от частоты, а будет
определяться, как обычно, на постоянном токе (по закону Ома).
Для тензорного анализа электромагнитных процессов введем
в
-мерном
дифференциально-геометрическом многообразии систему локальных
базисных векторов:
(2)
где
в общем случае произвольные координаты. Теперь умножим первое
уравнение в (1) на
,
второе уравнение умножим на
и т.д. Последнее уравнение в (1) умножим на
.
В результате получим систему из
уравнений:
(3)
Заметим, что в системе (3)
и
рассматриваются уже как функции точки (подобно векторам напряжённости
и индукции электрического поля, векторам напряжённости и индукции
магнитного поля в электродинамике), а не просто как переменные
состояния, то есть вводятся функциональные зависимости переменных от
координат:
(4)
(5)
Далее все левые части в (3) сложим:
(6)
Сумму
(7)
в (6) с точки зрения тензорного анализа можно представить абсолютным вектором (векторным полем):
(8)
Но, вместе с тем, нельзя то же самое сделать с суммой
(9)
и, тем самым, ввести в уравнение (6) (по аналогии с (8)) абсолютный вектор потокосцепления
(10)
потому что векторы (2) локального базиса нельзя в общем случае внести под знак производных, так как эти векторы зависят от координат, а координаты в общем случае зависят от времени, то есть, вообще говоря,
(11)
В подобных случаях в тензорном анализе вводят понятие ковариантного дифференцирования. Рассмотрим это понятие в рамках данного подхода.
Продифференцируем (10) по обычным правилам дифференцирования производных от произведения функций:
(12)
Поскольку в (12) по индексу
осуществляется суммирование, то этот индекс во втором слагаемом
правой части можно (это удобно для дальнейших преобразований)
заменить на любой другой, например, на
:
(13)
В (13) появились дифференциалы локалных базисных
векторов (
).
Эти дифференциалы, как известно из обычного анализа, можно выразить
через частные производные:
(14)
Вместе с тем, согласно тензорному анализу, частные
производные
могут быть представлены в следующем виде:
(15)
где
коэффициенты связности (то есть трёхиндексные символы Кристоффеля
второго рода).
Подставим (15) в (14). Тогда
(16)
Теперь подставим (16) в (13):
(17)
Кроме того, разделим левую и правую части (17) на дифференциал времени:
(18)
Из (18) следует
(19)
Подставим (19) и (8) в (6). В результате получим следующее уравнение:
(20)
Чтобы избавиться от производных от координатам, и, тем
самым, упростить полученное уравнение, произведём суммирование в (20)
по индексу
.
Тогда уравнение примет следующий более простой вид
(21)
где
(22)
По смыслу всего изложенного слагаемые
(23)
и
(24)
в (20) и (21), соответственно, являются математическим выражением физического процесса вытеснения тока в стержнях ротора. Это значит, что нелинейный электромагнитный процесс вытеснения тока математически может быть представлен в многомерном пространстве с кривизной (в дифференциально-геометрическом многообразии по терминологии тензорного анализа).
Если все
и, соответственно, все
равны нулю, то это значит, что частота тока ротора АД стремиться к
нулю, вытеснение тока в стержнях ротора отсутствует, а уравнения (20)
и (21) принимают один и тот же вид:
(25)
Равенство нулю всех
и
означает, что
-мерное
пространство является плоским (то есть без кривизны). Поэтому
локальные базисные векторы
в плоском пространстве не зависят от координат
,
как и векторы
и
.
Это значит, что в пространстве
измерений можно ввести подпространство двух измерений и ортогональную
двухмерную систему координат. Тогда уравнение (25) превращается в
обычную систему, состоящую из двух уравнений:
(26)
где
компоненты вектора потокосцепления ротора в ортогональной системе
координат
;
компоненты вектора тока ротора в той же системе координат;
сопротивление статора. Таким образом, в данном подходе принцип
соответствия соблюдается: уравнения более общей теории преобразуются
в уравнения частной теории, если допущения частной теории применить к
уравнениям более общей теории.
Векторы
и
в уравнении (21) тоже можно спроецировать на двухмерное ортогональное
подпространство. В этом случае каждый из этих векторов будет иметь по
две компоненты, а
будет содержать четыре компоненты. Система уравнений для ротора
примет в этом случае следующий вид:
(27)
где
компоненты вектора потокосцепления ротора в ортогональной системе
координат;
компоненты вектора тока ротора в той же системе координат;
компоненты, значения которых зависят в основном от эффективного
сечения стержней и от температуры ротора;
компоненты, численные значения которых определяются изменением фазы
вектора плотности тока ротора. Значения всех четырех компонент можно
принимать в первом приближении линейными функциями скольжения.
Заключение.
В настоящее время основной математической моделью, применяемой на практике, является модель Парка. Однако эта модель справедлива только при постоянных параметрах двигателя. Причём в этой модели не учитывается эффект вытеснения тока в стержнях ротора. Существуют другие математические модели, описывающие электромагнитные процессы в АД, в том числе и скин-эффект, но они, как правило, недостаточно обоснованы с теоретической точки зрения, а являются чисто инженерными решениями.
В данной статье предложена структура уравнений (27) электромагнитных процессов в роторе АД, обоснованная строго математически. Эта модель была неоднократно проверена методом математического моделирования и экспериментально, в том числе в системе векторного управления асинхронным электроприводом. Тип двигателя в экспериментальной установке 4А112МА6У3; мощность 3 кВт; параметры двигателя: активное сопротивление статора 2,16 Ом; активное сопротивление ротора 1,75 Ом; индуктивность статора 0,186 Гн; индуктивность ротора 0,189 Гн; индуктивность намагничивающего контура 0,18 Гн; момент инерции ротора 0,017 кгм2; число пар полюсов 3.