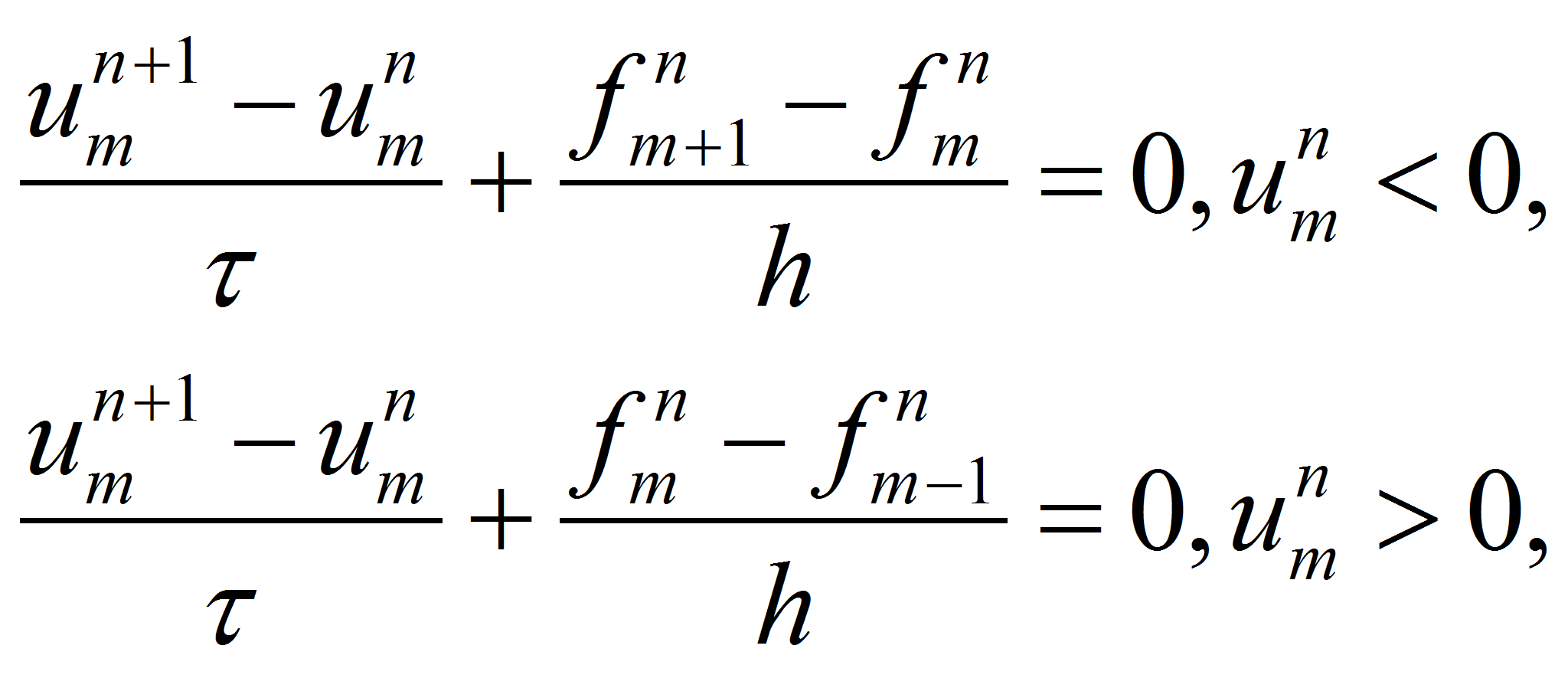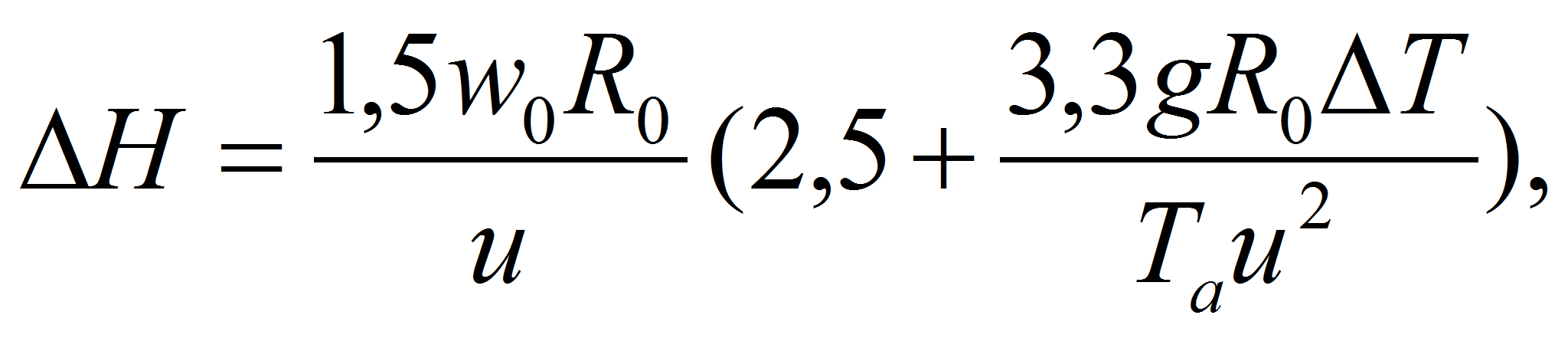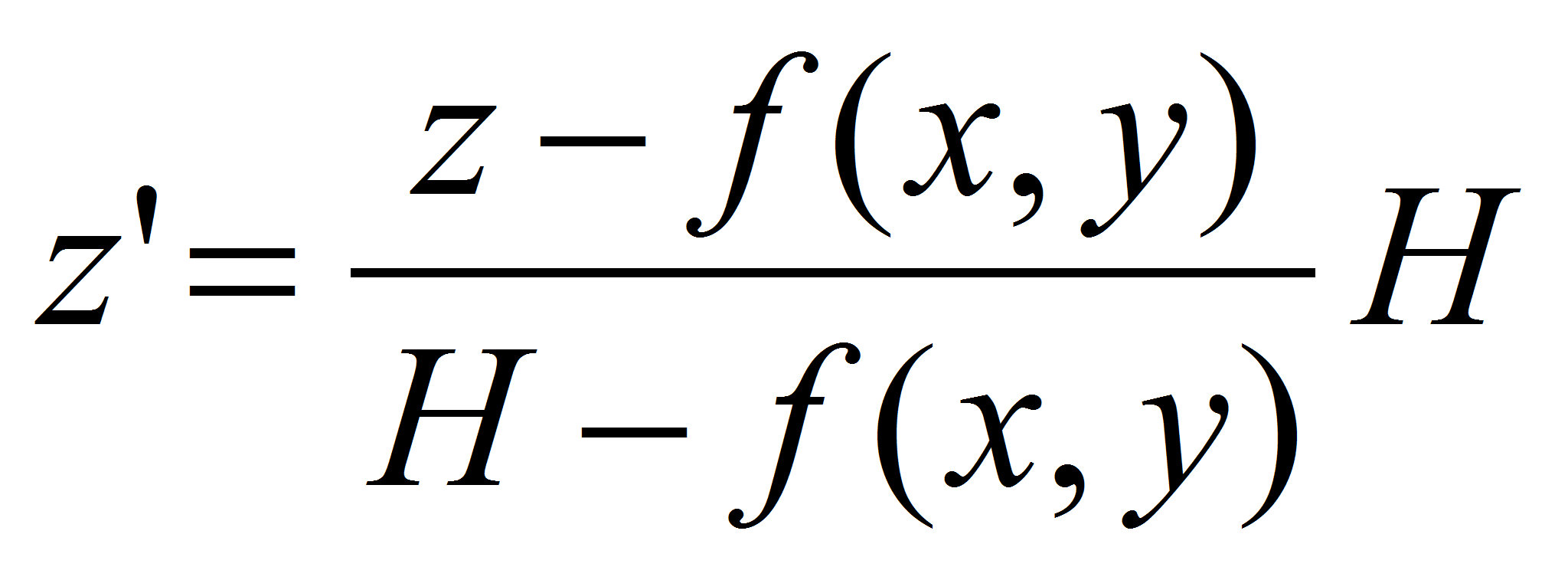Использование технологии OpenMP в распределенной системе экологического мониторинга

Экологический мониторинг является одной из важнейших задач в деятельности промышленного предприятия. Система прогнозирования распространения выбросов вредных веществ является одним из ключевых компонентов системы экологического мониторинга.

Постановка задачи

Необходимо рассчитать в трехмерном пространстве распространение выбросов с течением времени.

Входные данные:

1) направление ветра по розе ветров;

2) давление воздуха;

3) температура воздуха;

4) данные для расчета концентрации (количество вредного вещества, выбрасываемого в атмосферу и т.д.);

5) координаты выброса.

Выходными данными является величина концентрации вредных веществ во всех точках пространства в определенные моменты времени.

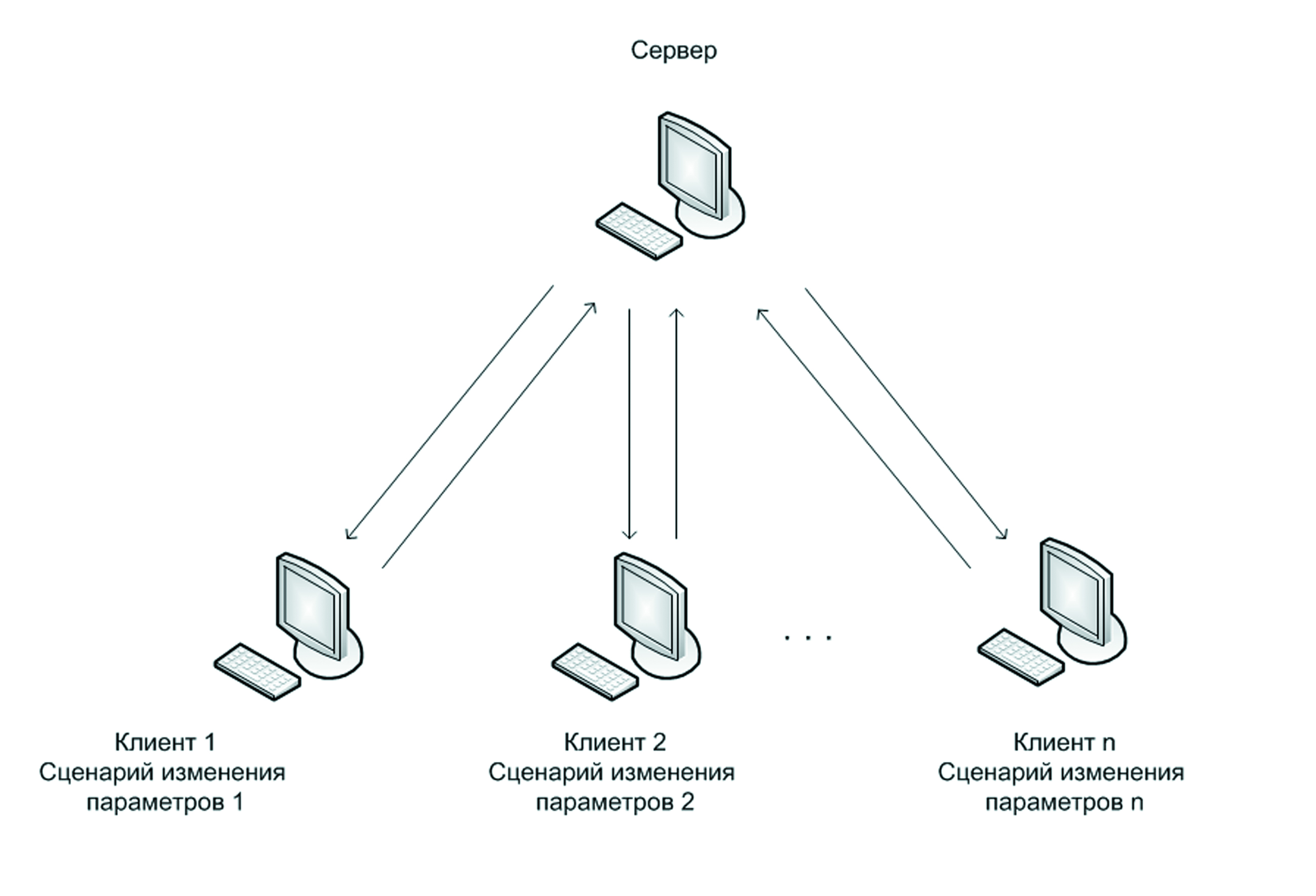
При решении данной задачи с помощью распределенной системы была выбрана архитектура, при которой каждый вычислительный узел рассчитывает матрицу концентраций со своими входными параметрами. В рамках данной работы необходимо определить входные параметры дополнительных вычислительных узлов и схему их взаимодействия.

Разностная схема

Схема Куранта - Изаксона – Риса (КИР). Обобщение схем КИР на квазилинейный случай (при использовании дивергентной формы записи уравнения Хопфа):

где u – искомая функция концентрации, f - функция описывающая источник дыма,– шаг по времени, h – шаг в пространстве.

Рис. 1. Архитектура системы.

Схема устойчива при выполнении условия Куранта:

(если условие не выполняется, решение может не сойтись)

Вследствие перегретости, примесь в начальной фазе своего распространения обладает восходящей скоростью, но эта начальная фаза непродолжительна, т. к. под действием турбулентности температуры частиц примеси и воздушной среды быстро выравниваются. Точно учесть указанный эффект чрезвычайно трудно, так как пришлось бы решать совместно уравнения диффузии и свободной конвекции частиц газа. Однако даже при значительных перегревах газа этот эффект можно учесть приближенно, заменяя реальный источник примеси геометрической высоты H фиктивным, несколько приподнятым источником, высота которого ∆H [1].

Существует большое количество полуэмпирических и эмпирических формул, предложенных разными авторами для определения ∆H . По проведенным оценкам [3] наиболее приемлемо ∆H определяется для нейтральной стратификации атмосферы по формулам Пристли, Спэра, Берлянда, Дановича–Зайгеля. В связи со сказанным для определения начального подъема ∆H газовой струи была выбрана следующая полуэмпирическая формула [4]:

где T_в, T_α – соответственно температуры выбросов газа и окружающего воздуха по абсолютной шкале, w – начальная скорость выброса газов, R – радиус устья трубы, g – ускорение свободного падения, u – скорость ветра на высоте флюгера.

Рассчитываем ∆H, это фактически расстояние на котором газ остынет и начнёт опускаться. Значит вокруг трубы можно выделить сферу радиуса ∆H с вертикальными скоростями направленными вверх причём в центре сферы скорость подъёма равна начальной скорости газа, а на границах нулю.

Учёт ландшафта осуществляется вследствие введения новой системы координат:

,

где H – верхняя граница расчёта, f(x,y) – функция высот ландшафта

В такой системе координат ландшафт должен быть гладким, производная должна быть монотонной, иначе в местах перепадов не будет выполняться условие Куранта и решение может расходиться. А на гладких ландшафтах учёт ландшафта не заметен [2].

Описание эксперимента

Испытания проводились на вычислительном кластере кафедры ЭВМиСВолгГТУ, а именно на 64-ядерном процессоре Intel. Расчеты проводились при следующих входных параметрах:

1. размерность сетки 300*300*100;

2. размерность сетки 600*600*200;

3. размерность сетки 900*900*300.

Рассчитываемые прогнозы:

1. краткосрочный(30 минут);

2. долгосрочный(120 минут).

Основным исследуемым параметром в данном эксперименте является зависимость времени построения прогноза от количества вычислительных процессов, а также зависимость ускорения работы программы от количества вычислительных процессов.

Таблица 1

Результаты выполнения программы при размерностях вычислительной сетки 300*300*100 приведены в таблице 1. Из результатов следует, что ускорение растет прямо пропорционально количеству вычислительных процессов, однако заметно падение роста ускорения при использовании тридцати двух вычислительных потоков. Данное явление связано с тем, что издержки создания дополнительных потоков замедляют выполнение программы.

Таблица 2

Результаты выполнения программы при размерностях вычислительной сетки 600*600*200 приведены в таблице 2. Здесь также просматривается падение роста ускорения при использовании тридцати двух вычислительных потоков.

Таблица 3

Результаты выполнения программы при размерностях вычислительной сетки 900*900*300 приведены в таблице 3. В данном случаенеобходимо отметить нелинейное ускорение при переходе от последовательной версии программы к параллельной.

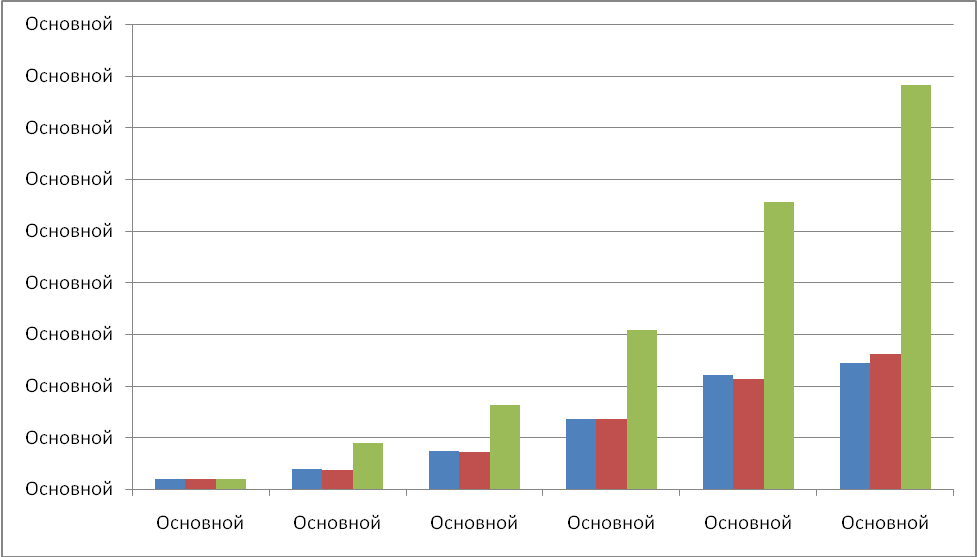
Рисунок 2 - Величина ускорения для каждой вычислительной сетки

Выводы

На рисунке 2 изображены значения ускорений для каждой вычислительной сетки в порядке их описания в статье. Наибольшее значение ускорения получено при использовании сетки размерностью 900*900*300. Данное явление связано с нелинейным ускорением выполнения параллельной программы, которое обусловлено особенностями использования оперативной памяти.

Литература:

1. Алексеев В.A. Адаптивный экологический мониторинг окружающей среды / В.A. Алексеев, А.В. Арефьев// Экология и промышленность России.—2003. — № 10.—С. 11-13.

2. Алоян А.Е. Динамика и кинетика газовых примесей и аэрозолей в атмосфере. — М.: ИВМ РАН, 2002. —201 с.

3. Бем Б. Результаты экспериментального исследования дымовых струй от тепловых электростанций // Метеорологические аспекты загрязнения атмосферы. — Л.: ГИМИЗ, 1971 — С.44-48.

4. Берлянд М. Е. Современные проблемы атмосферной диффузии и загрязнения атмосферы. Л.: Гидрометеоиздат,1975. —448 с.