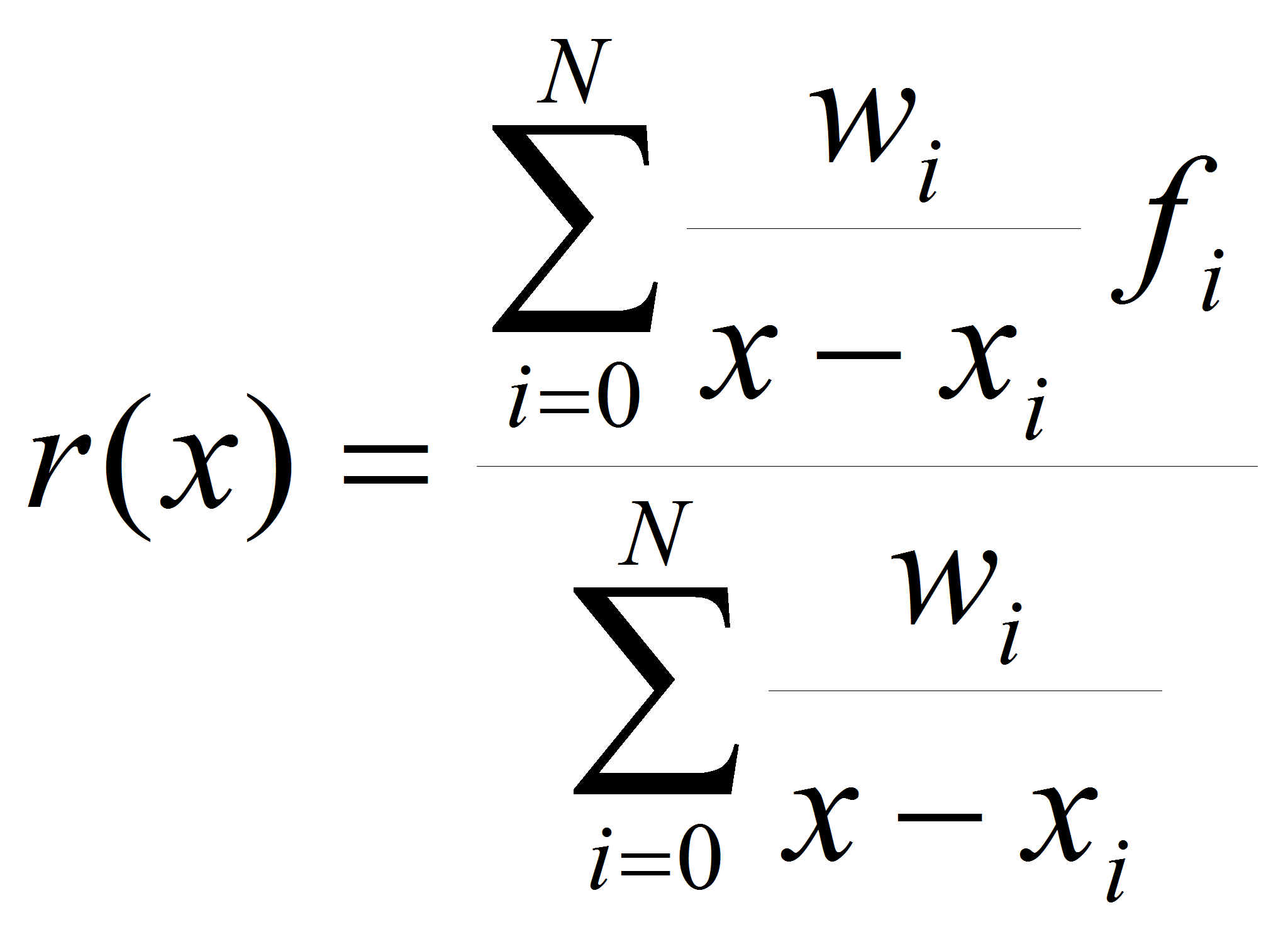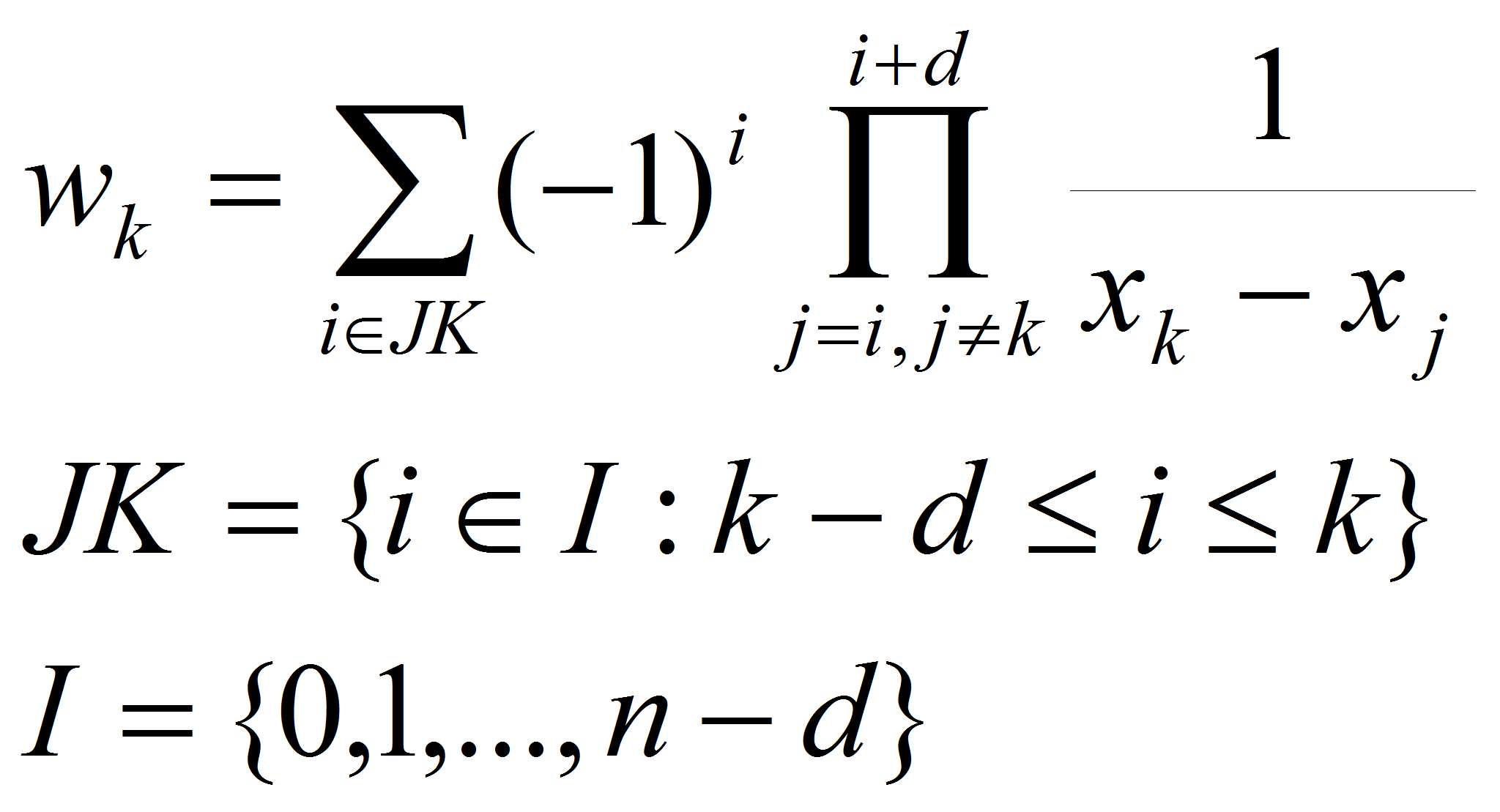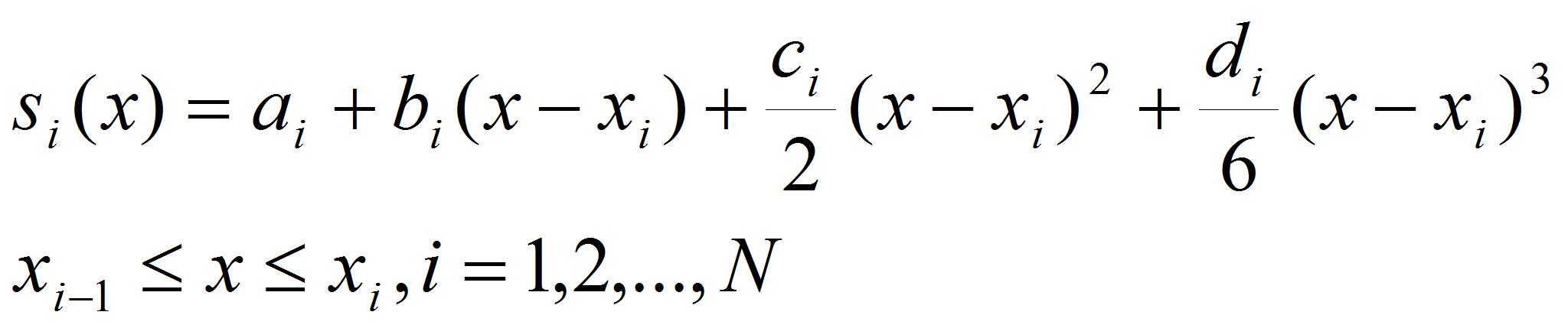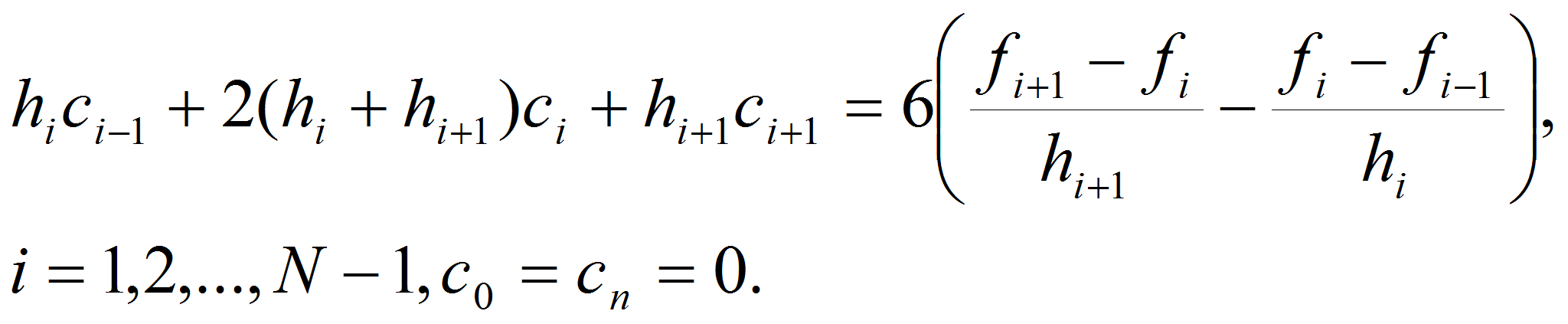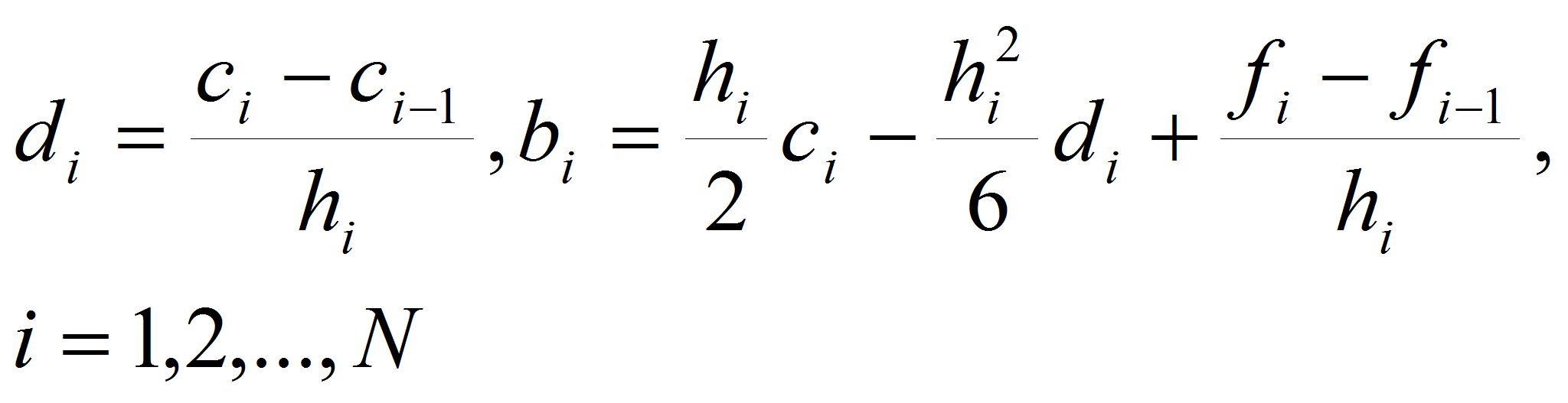- Электронные архивы позволяют предприятиям в структурированном виде накапливать информацию, содержащуюся в документах. Занесение документов осуществляется по схеме, описанной в статье [1], при этом документ проходит через этапы сканирования, распознавания, верификации и собственно занесения в архив. В статье [2] описаны методы решения задачи поиска ассоциаций в электронном архиве. Это помогает ускорить процесс верификации документов, соответственно, уменьшить время занесения в архив. Накопленные же документы можно использовать не только в повседневной работе организации, но и для выявления некоторых тенденций и составления прогнозов развития. В данной статье рассмотрим методы решения задачи прогнозирования, используя некоторую кластеризацию архива.
- Итак, в архиве накоплено некоторое количество документов, атрибуты которых принимают значения разных типов: число, дата/время, строка и др. Необходимо предсказать значения атрибутов для будущих документов. Например, имеются данные о суммах в договорах, необходимо выявить тенденцию и предположить значения сумм последующих договоров. Для этого можно использовать методы аппроксимации и экстраполяции. Но сначала необходимо разбить исходное множество документов на группы, то есть произвести кластеризацию. Рассмотрим этот момент подробнее.
-
Во-первых, первоначальное разбиение на группы уже
выполнено в архиве делением документов на типы. Однако к одному типу
может относиться довольно большое количество документов, поэтому
необходим дополнительный признак. В статье [2] описаны методы
создания справочника значений – таблицы наиболее часто
встречающихся пар значений атрибутов. Строго говоря, справочник –
это некоторый набор экземпляров правил вида «Если
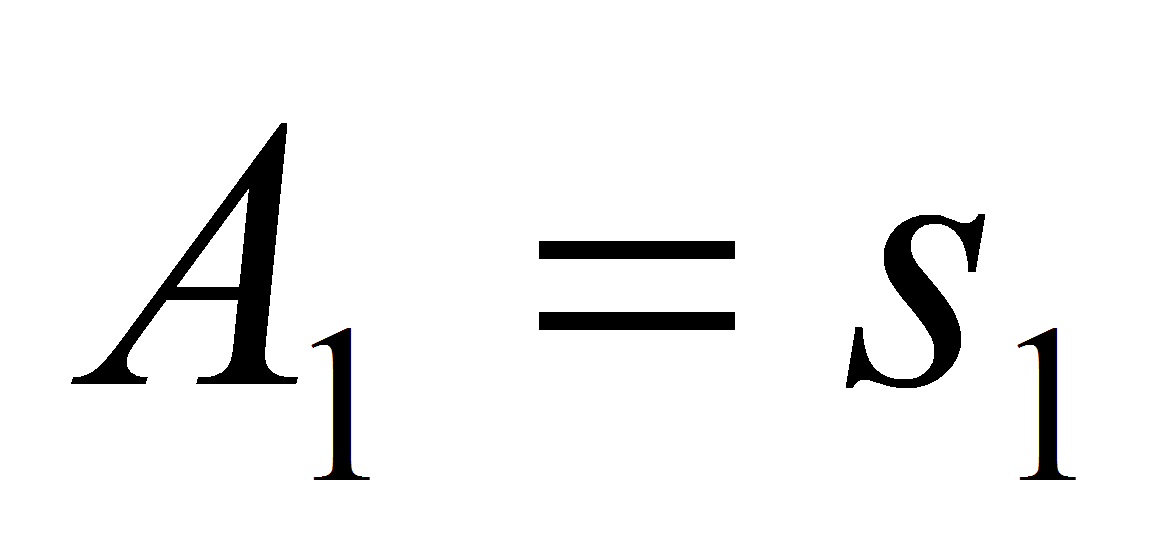 ,
то
,
то
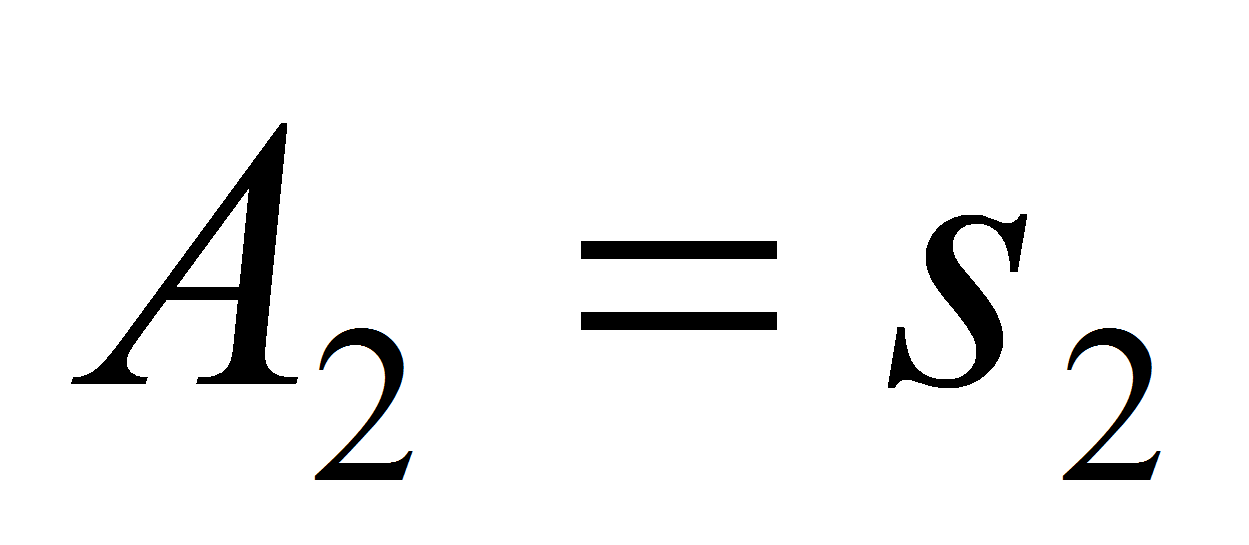 с вероятностью
с вероятностью
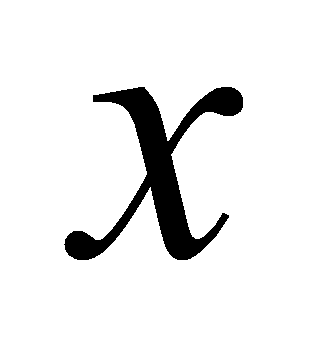 ».
Здесь
».
Здесь
 и
и
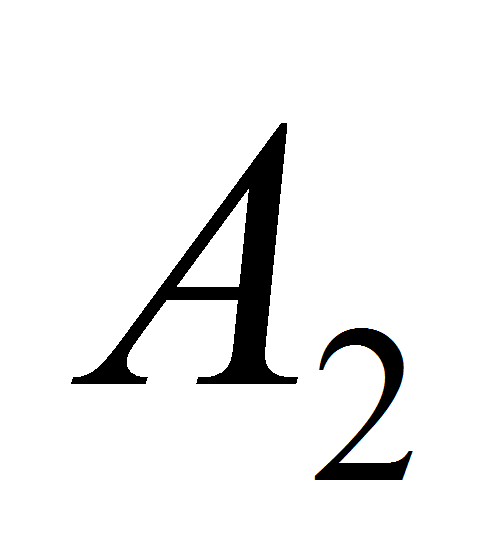 -
некоторые атрибуты,
-
некоторые атрибуты,
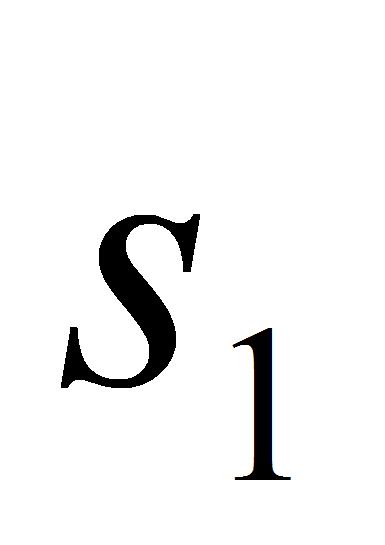 и
и
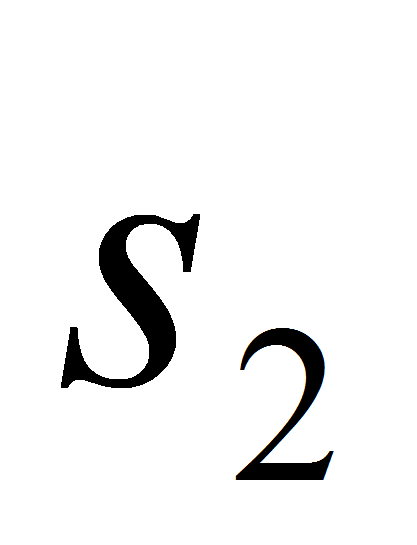 -
значения атрибутов,
-
значения атрибутов,
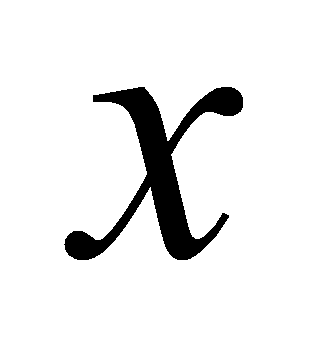 - численное значение вероятности. Для получения справочника можно
использовать следующие методы:
- численное значение вероятности. Для получения справочника можно
использовать следующие методы:
- метод полного вероятностного справочника, описывающий вероятности всех встречающихся пар значений;
- метод складывающихся столбцов, являющийся более быстрым, но менее точным за счет использования некоторых средних значений;
- метод ограничивающей выборки, комбинирующий два предыдущих.
- Рассмотрим пример. Пусть в некотором документе имеются поля «Организация» и «Адрес организации». Часто бывает, что одна и та же организация в разных документах обозначается по-разному, например, в результате сокращений и аббревиатур (ОАО «ЭЦМ» и ОАО «Электроцентромонтаж»). В таком случае, если адрес записан одинаково (не считая разных регистров букв и знаков препинания), он может однозначно идентифицировать организацию.
-
Итак, выберем некий атрибут
 как основной и применим один из предложенных методов для создания
справочника. На его основе начнем создавать кластер. Выберем
некоторое значение
как основной и применим один из предложенных методов для создания
справочника. На его основе начнем создавать кластер. Выберем
некоторое значение
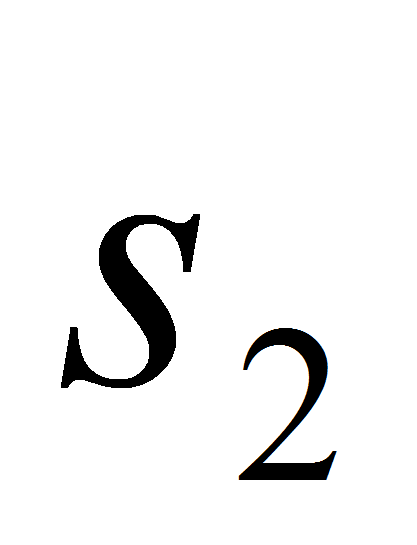 атрибута
атрибута
 ,
еще не использованное в каких-либо кластерах, и включим его в
множество
,
еще не использованное в каких-либо кластерах, и включим его в
множество
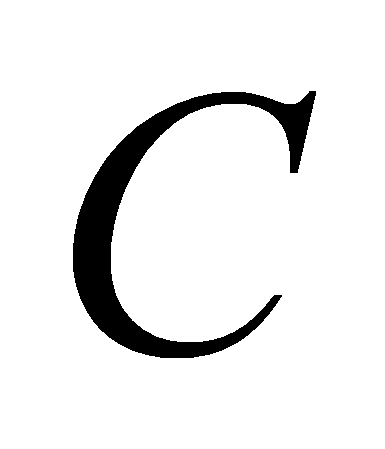 (англ.
consequence - следствие). Следующее
действие назовем шагом кластеризации:
(англ.
consequence - следствие). Следующее
действие назовем шагом кластеризации: -
Для всех элементов
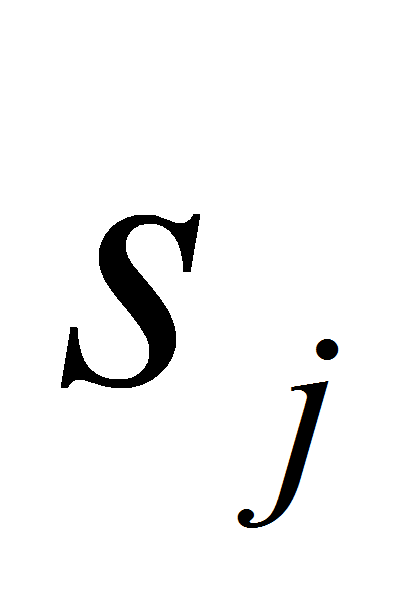 множества
множества
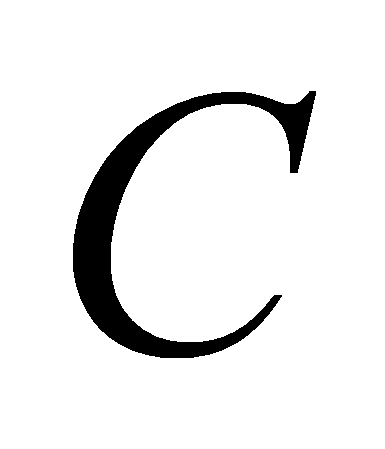 найдем в наборе все экземпляры правил, в которых значение атрибута
найдем в наборе все экземпляры правил, в которых значение атрибута
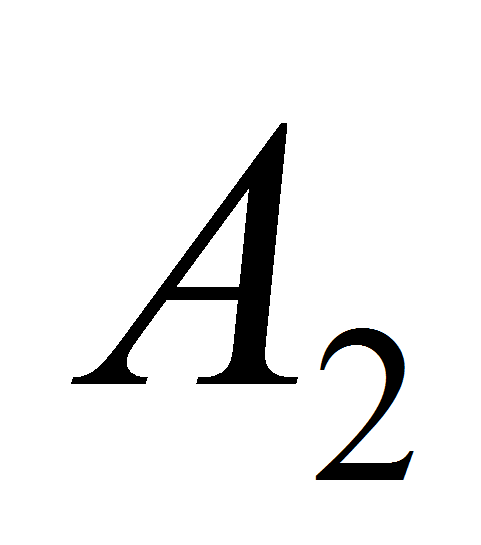 равно
равно
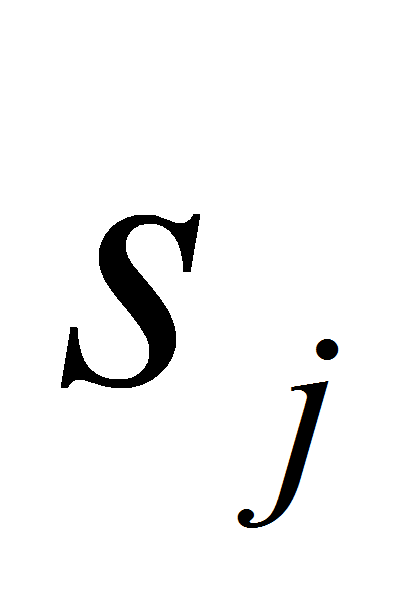 ,
то есть правила вида «Если
,
то есть правила вида «Если
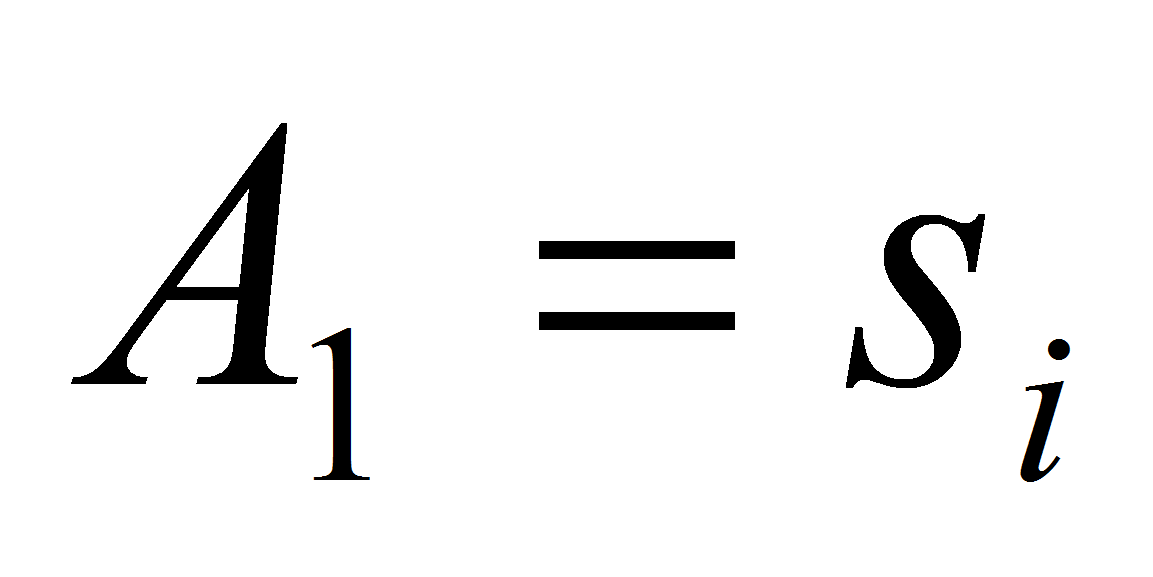 ,
то
,
то
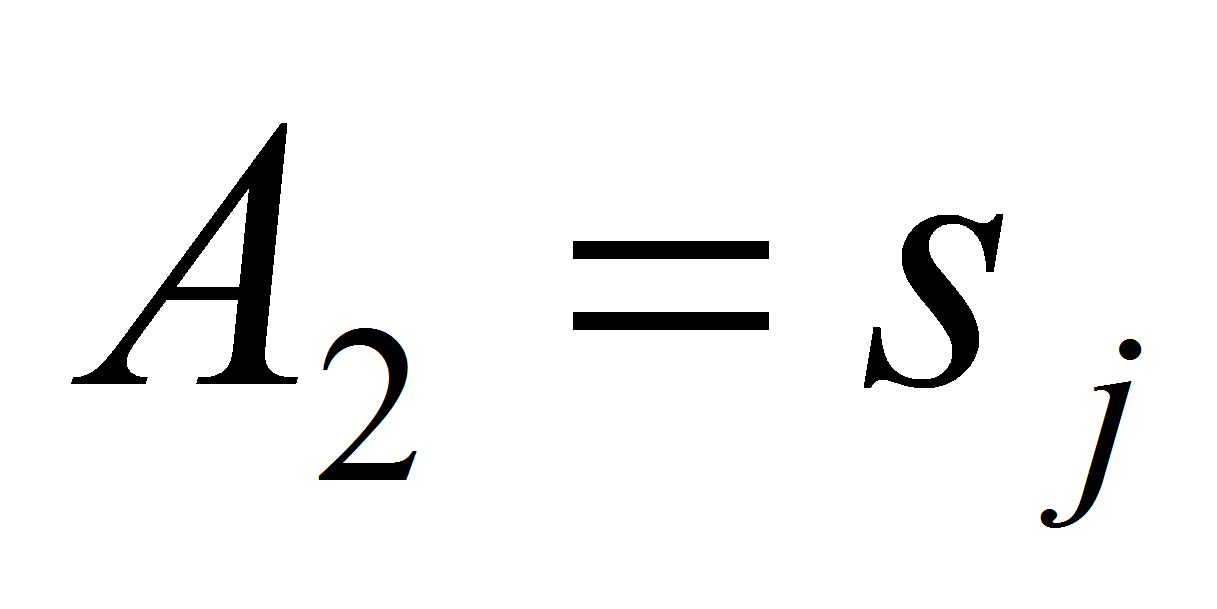 с вероятностью
с вероятностью
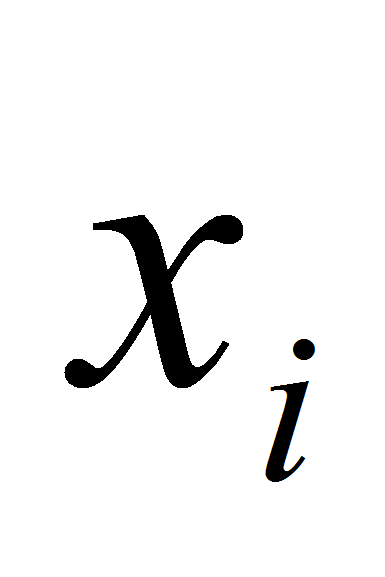 »,
где
»,
где
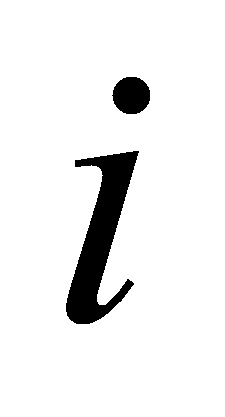 – некоторый номер значения. Все значения
– некоторый номер значения. Все значения
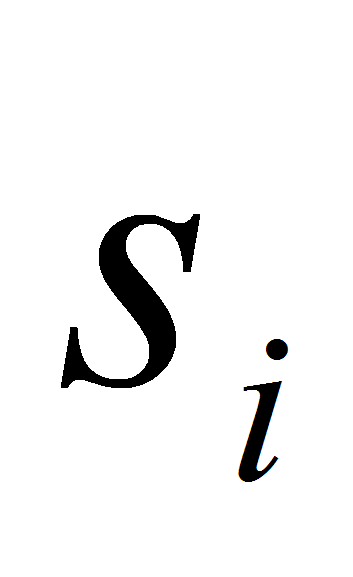 включим в множество
включим в множество
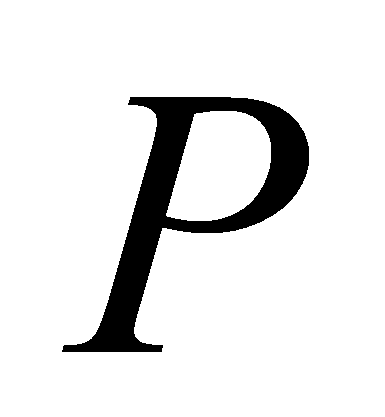 (англ.
premise - посылка). Далее для всех
элементов
(англ.
premise - посылка). Далее для всех
элементов
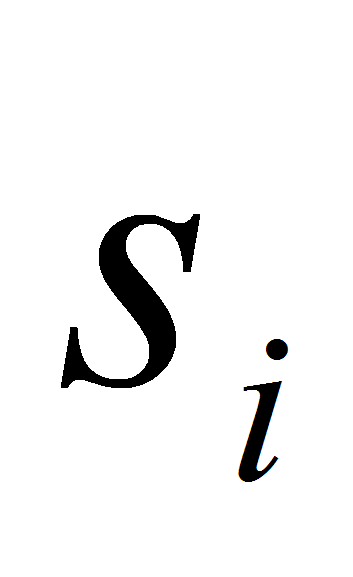 из множества
из множества
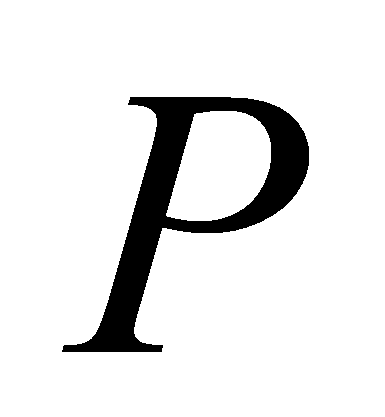 найдем все экземпляры правил, в которых значение атрибута
найдем все экземпляры правил, в которых значение атрибута
 равно
равно
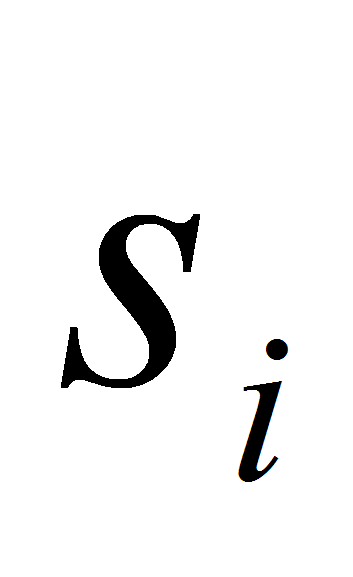 ,
то есть правила вида «Если
,
то есть правила вида «Если
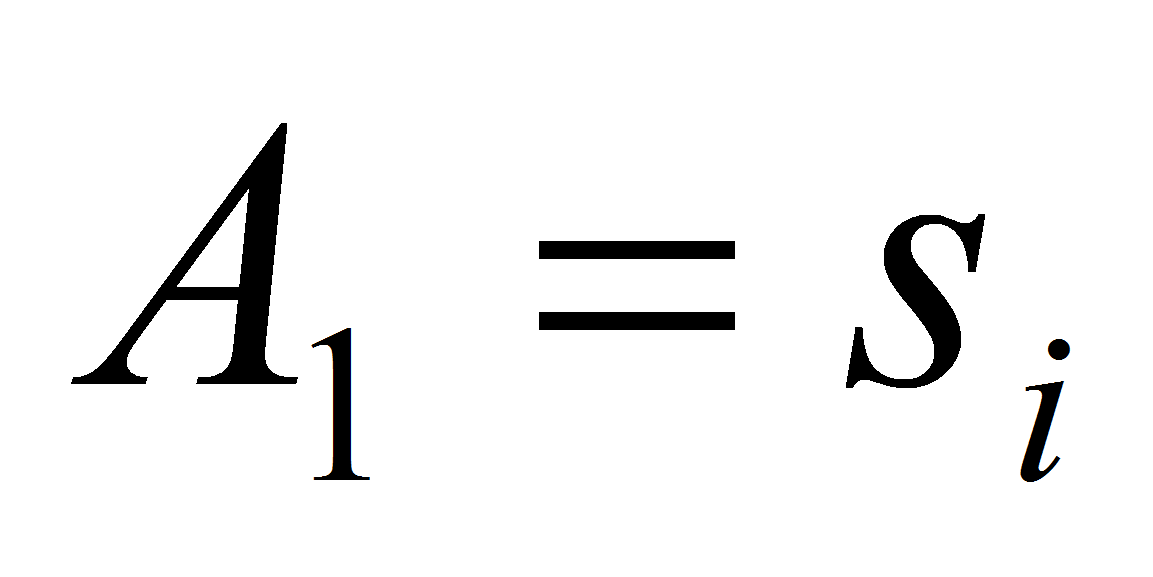 ,
то
,
то
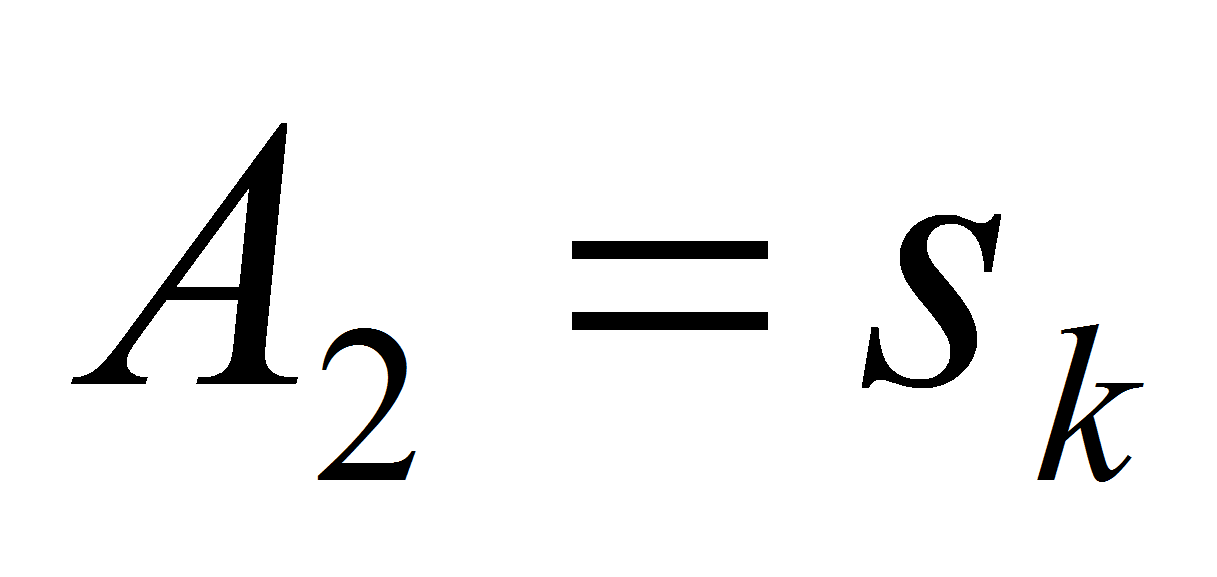 с вероятностью
с вероятностью
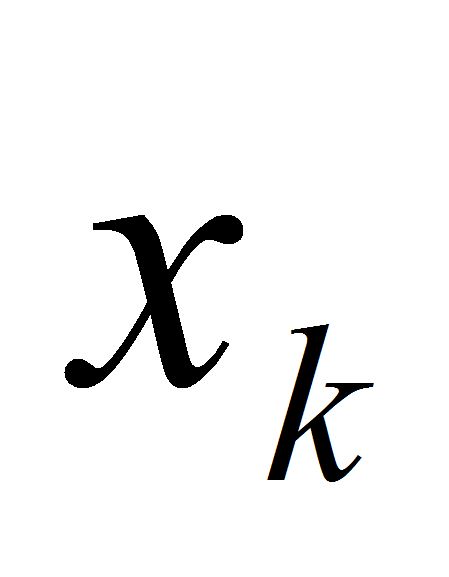 ».
Все значения
».
Все значения
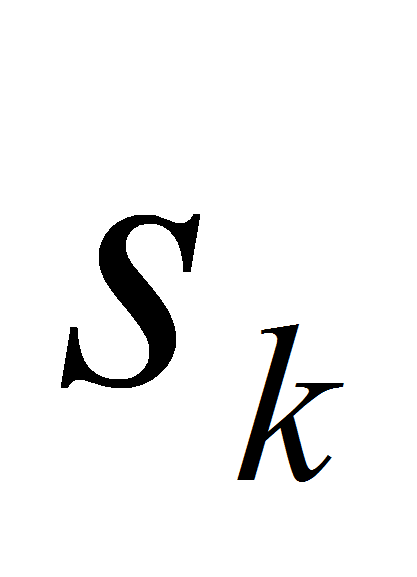 включим в множество
включим в множество
 .
Это и есть шаг кластеризации. Будем проводить его до тех пор, пока
на каком-либо шаге множество
.
Это и есть шаг кластеризации. Будем проводить его до тех пор, пока
на каком-либо шаге множество
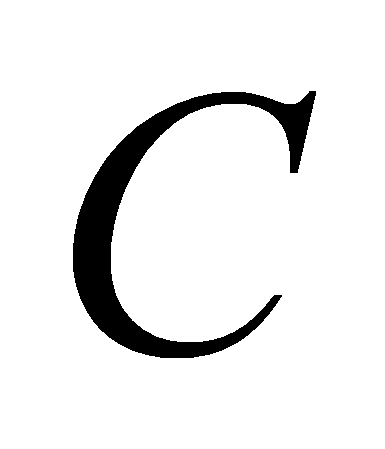 не останется неизменным, то есть новых элементов добавлено не было.
Соответственно в кластер объединяются те документы, для которых
выполняется равенство
не останется неизменным, то есть новых элементов добавлено не было.
Соответственно в кластер объединяются те документы, для которых
выполняется равенство
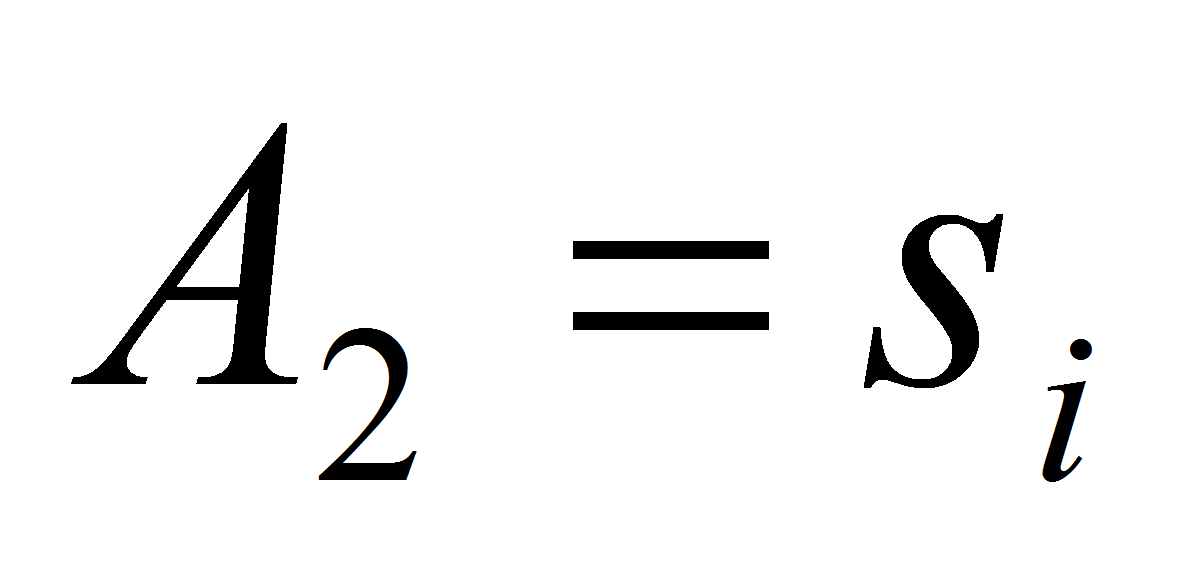 ,
где
,
где
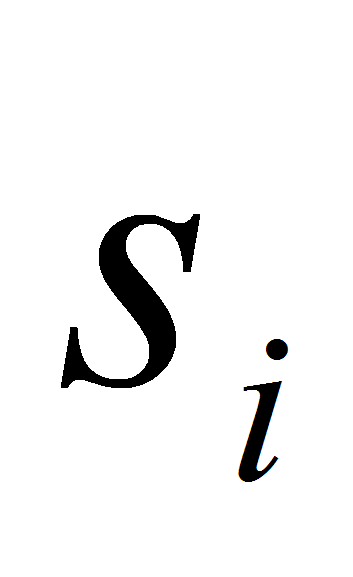 - элемент множества
- элемент множества
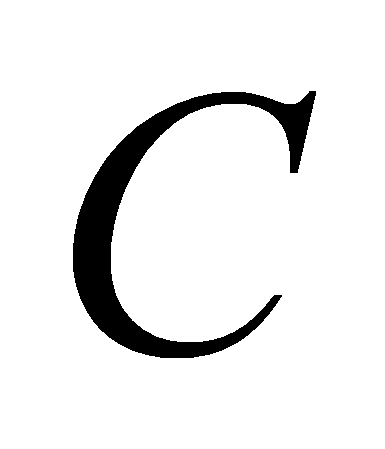 .
При составлении следующего кластера элементы множества
.
При составлении следующего кластера элементы множества
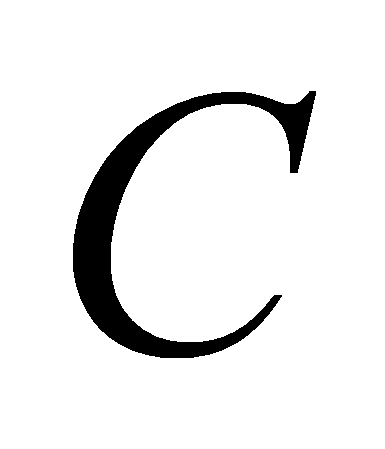 в рассмотрении не участвуют. Кластеры составляются до тех пор, пока
есть значения атрибута
в рассмотрении не участвуют. Кластеры составляются до тех пор, пока
есть значения атрибута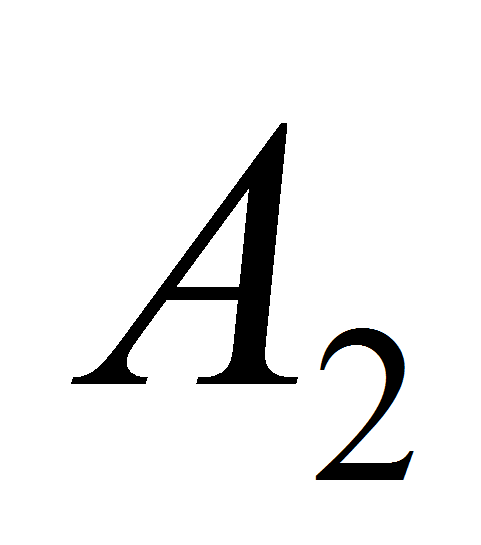 ,
не вошедшие ни в один кластер.
,
не вошедшие ни в один кластер.
- Возвращаясь к примеру, поясним. Справочник представляет собой некоторую таблицу пар «Наименование организации – Адрес организации». Начинаем работу с некоторого конкретного адреса. Найдем все наименования организации, соответствующие этому адресу. Затем всем этим наименованиям найдем соответствующие адреса, которые могут не совпадать по написанию с ранее учтенными. Если был найден новый вариант адреса, то повторим процедуру. В результате в кластер отбираются все варианты наименований и адресов одной и той же организации.
- Таким образом, исходное множество документов типа
оказывается разбитым на подмножества согласно значениям некоторого
атрибута
 .
Далее расположим документы по возрастанию даты, минимальную дату
примем за начало отсчета. Затем на оси времени, обозначим ее
.
Далее расположим документы по возрастанию даты, минимальную дату
примем за начало отсчета. Затем на оси времени, обозначим ее
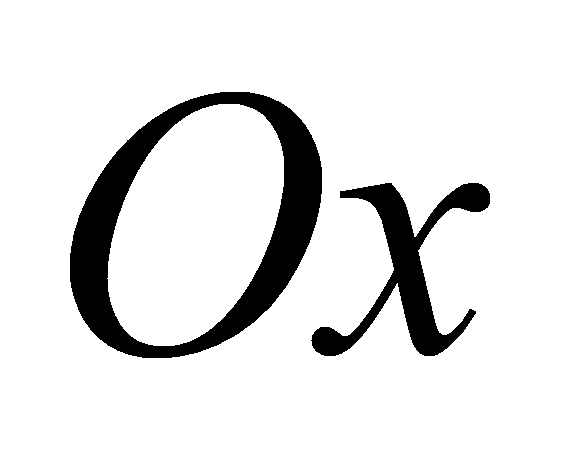 ,
будем откладывать некоторый период, принимаемый за единицу. В
качестве такого периода можно взять, например, 1 день, 1 месяц, 1
год или другое значение. Далее выберем числовой атрибут
,
будем откладывать некоторый период, принимаемый за единицу. В
качестве такого периода можно взять, например, 1 день, 1 месяц, 1
год или другое значение. Далее выберем числовой атрибут ,
значения которого необходимо предсказать. Таким образом, каждое
подобное подмножество представляет некоторую функцию, которую
следует аппроксимировать. Формально каждую такую функцию можно
записать в виде таблицы значений
,
значения которого необходимо предсказать. Таким образом, каждое
подобное подмножество представляет некоторую функцию, которую
следует аппроксимировать. Формально каждую такую функцию можно
записать в виде таблицы значений
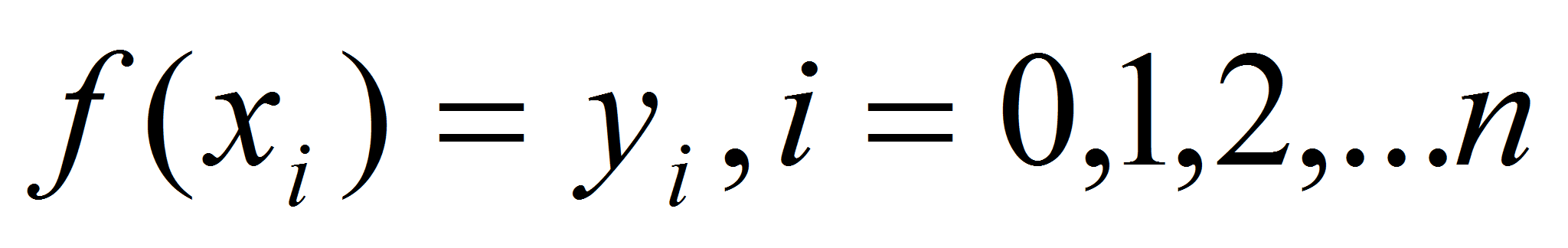 .
Необходимо найти значение функции при некотором
.
Необходимо найти значение функции при некотором
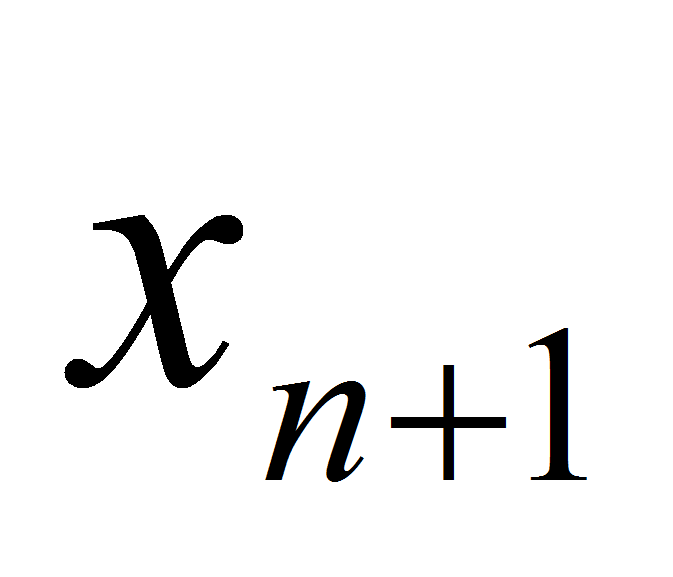 .
Для этого можно использовать методы экстраполяции, например,
следующие:
.
Для этого можно использовать методы экстраполяции, например,
следующие:
-
Формула Ньютона для экстраполяции вперед [3].
Эта формула используется, когда значения функции известны в узлах
сетки с постоянным шагом. Этот шаг обозначим через
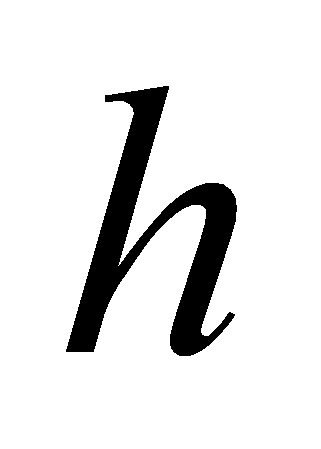 .
Тогда верна следующая формула
.
Тогда верна следующая формула
-
Интерполяционный многочлен Лагранжа [4]. При
применении этого метода узлы интерполяционной сетки не обязательно
должны быть равноотстоящими, а могут быть произвольно заданными.
Многочлен Лагранжа – это многочлен
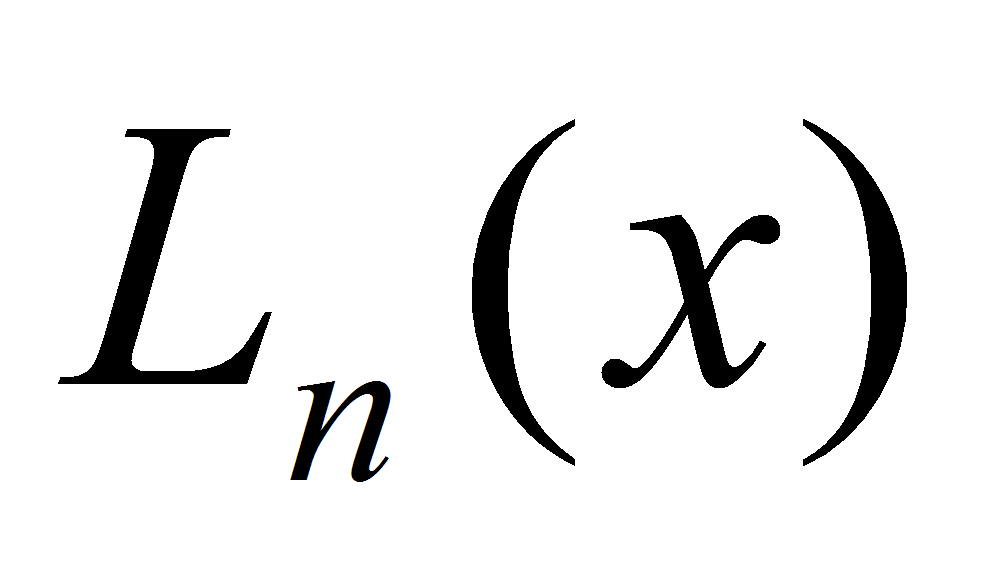 степени не выше
степени не выше
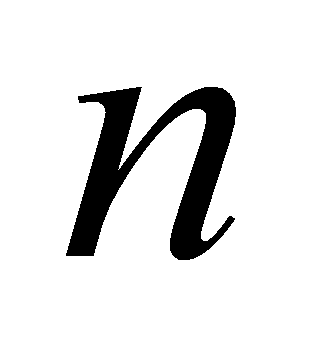 ,
принимающий в заданных узлах
,
принимающий в заданных узлах
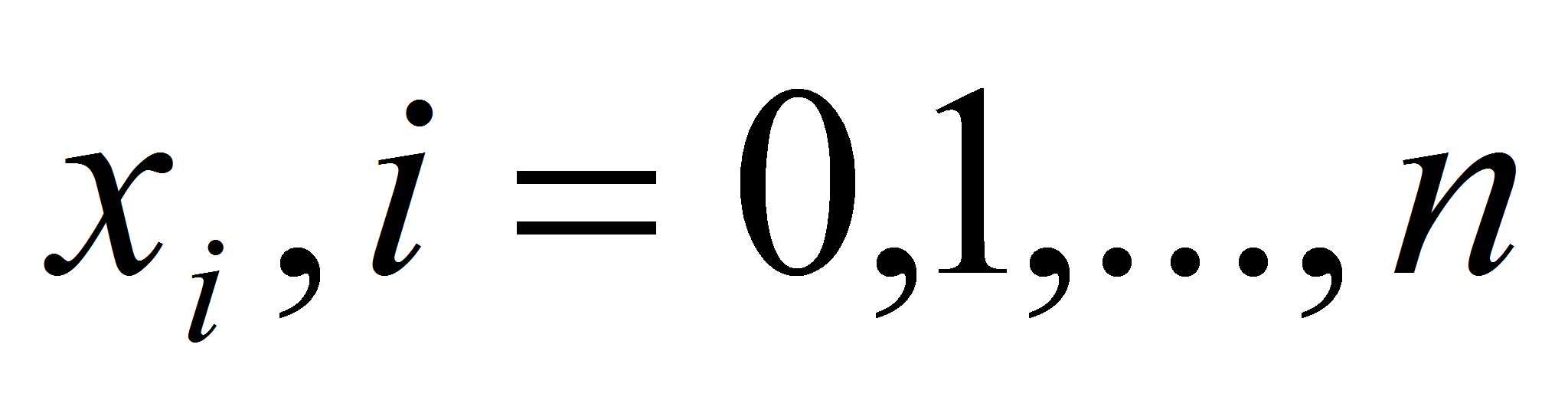 значения, совпадающие со значениями функции
значения, совпадающие со значениями функции
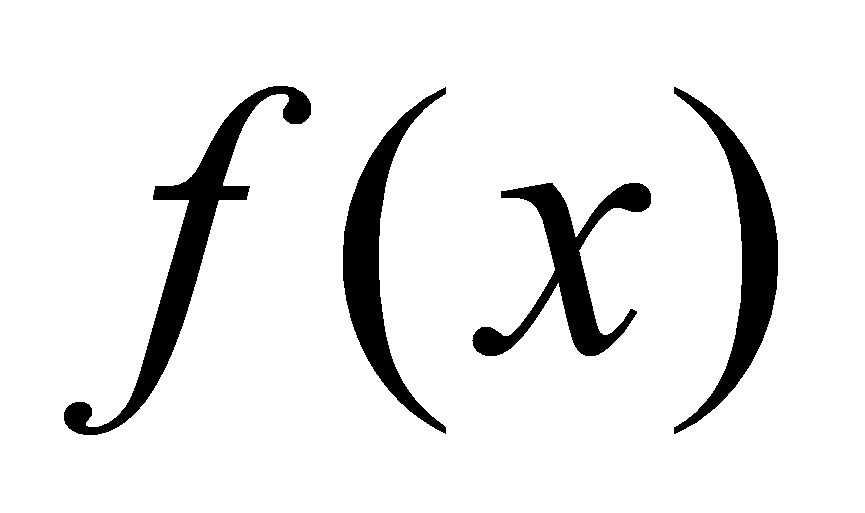 .
Такой многочлен определяется следующей формулой
.
Такой многочлен определяется следующей формулой
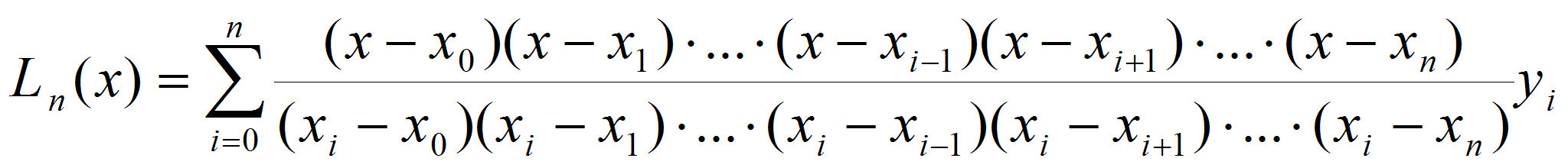 (3)
(3)- Этот многочлен является единственным, и его затем можно использовать для вычисления значений в других точках.
-
Методы рациональной интерполяции [5].
Интерполяция рациональными функциями заключается в представлении
искомой функции
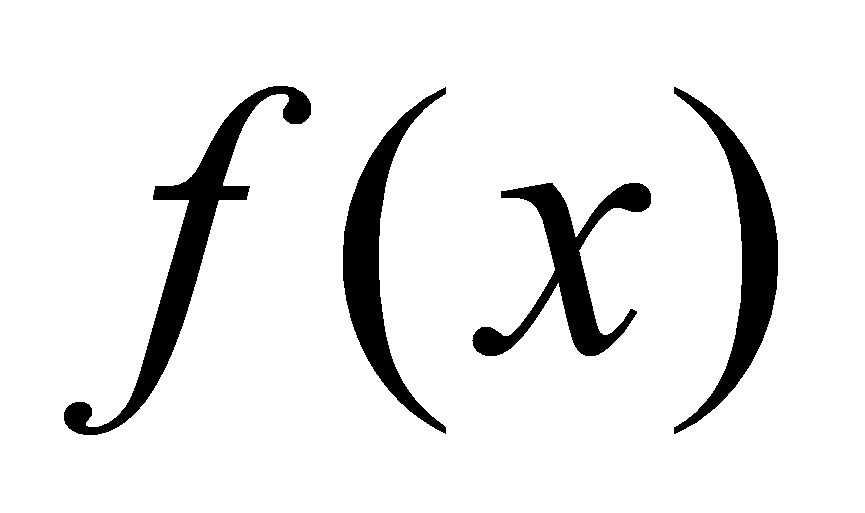 в виде отношения двух многочленов:
в виде отношения двух многочленов:
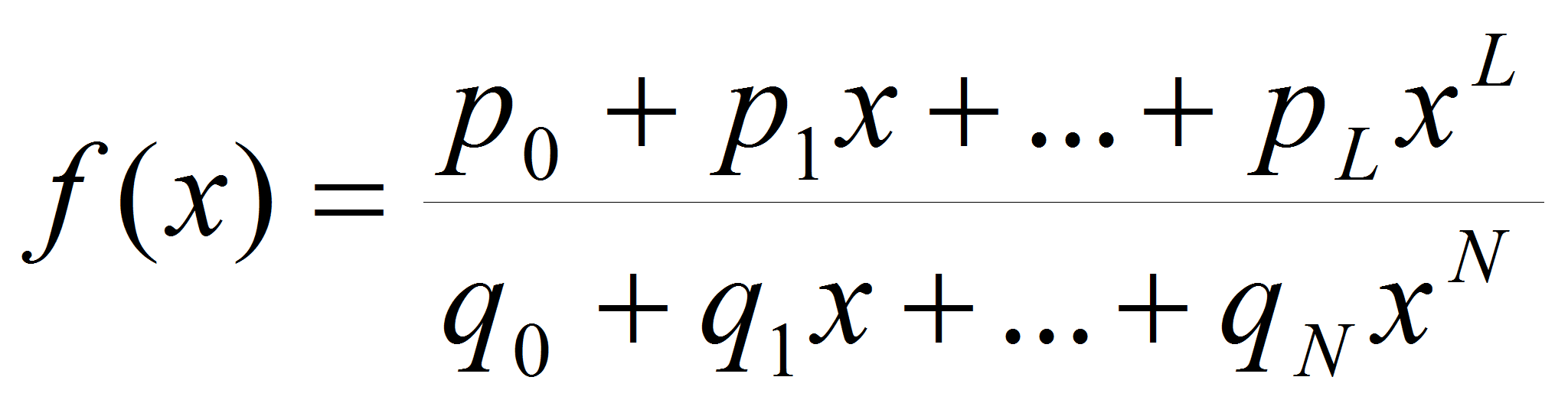 (4)
(4)-
Достоинствами такой интерполяции являются высокая
точность и неподверженность проблемам, свойственным полиномиальной
интерполяции. Однако одним из недостатков является то, что не для
каждого набора точек можно построить рациональную функцию. Одним из
алгоритмов для построения функции является алгоритм
Флоатера-Хорманна. Итак, пусть даны точки
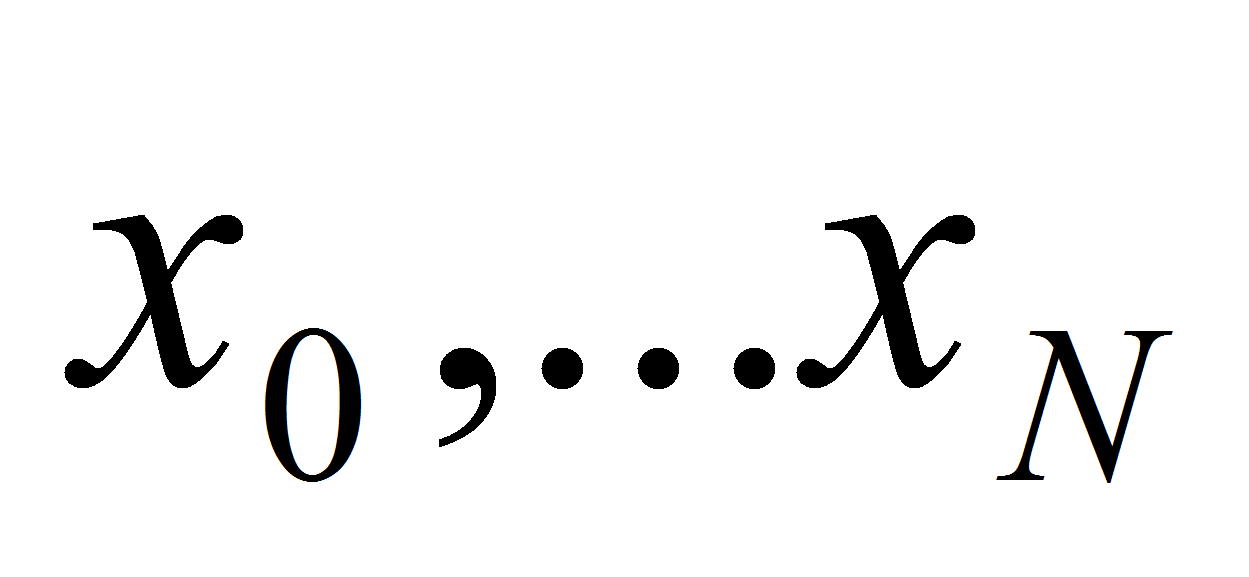 и даны значения функции в них:
и даны значения функции в них:
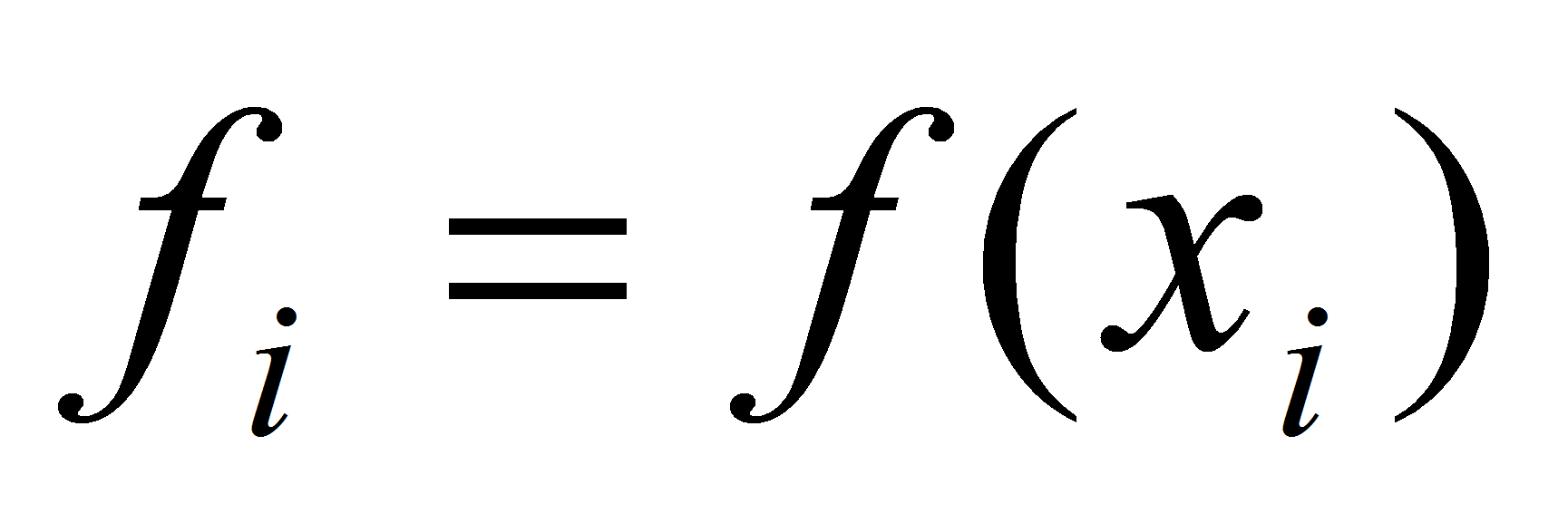 .
Пусть
.
Пусть
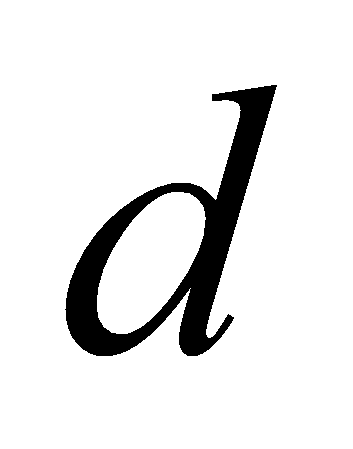 - порядок интерполяционной схемы Флоатера-Хорманна
- порядок интерполяционной схемы Флоатера-Хорманна
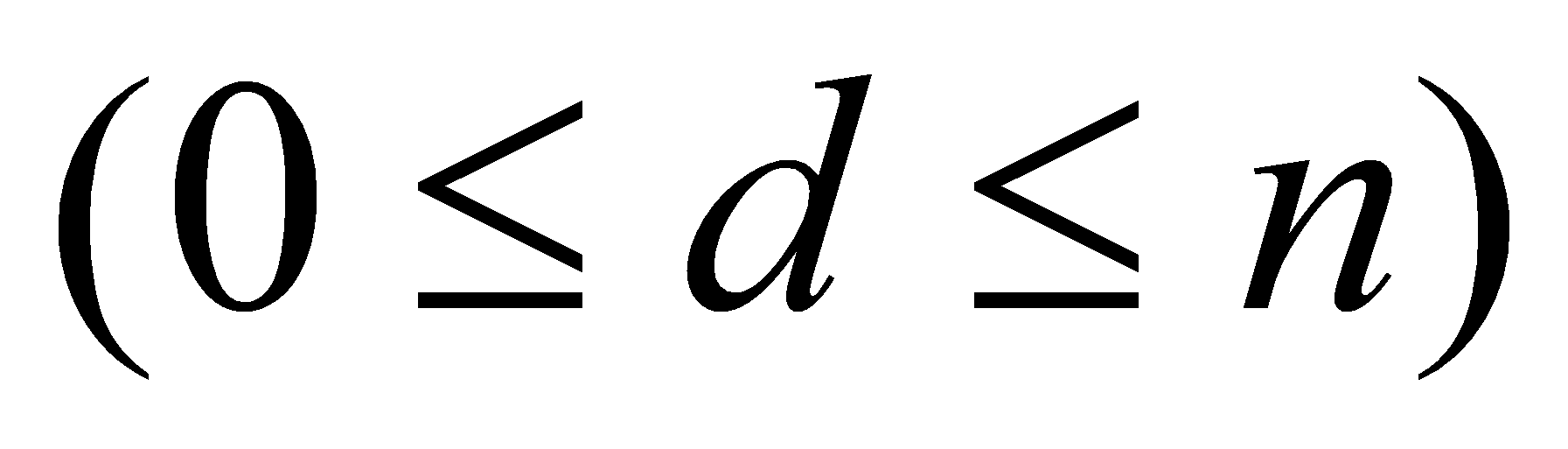 и пусть
и пусть
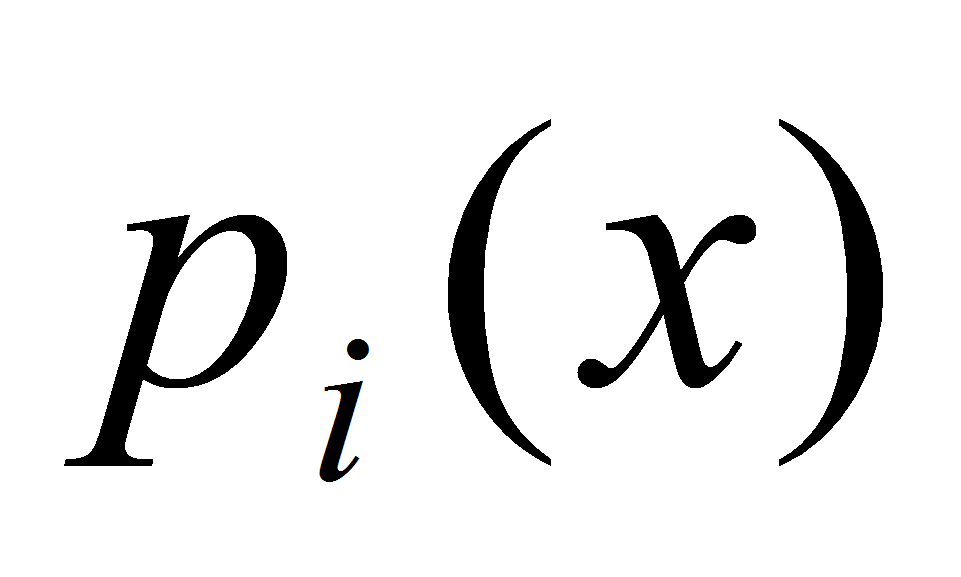 обозначает полином, интерполирующий функцию
обозначает полином, интерполирующий функцию
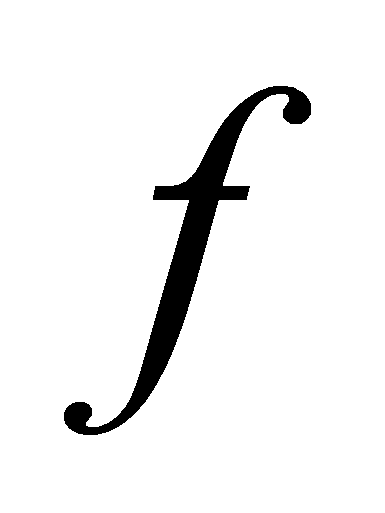 в точках
в точках
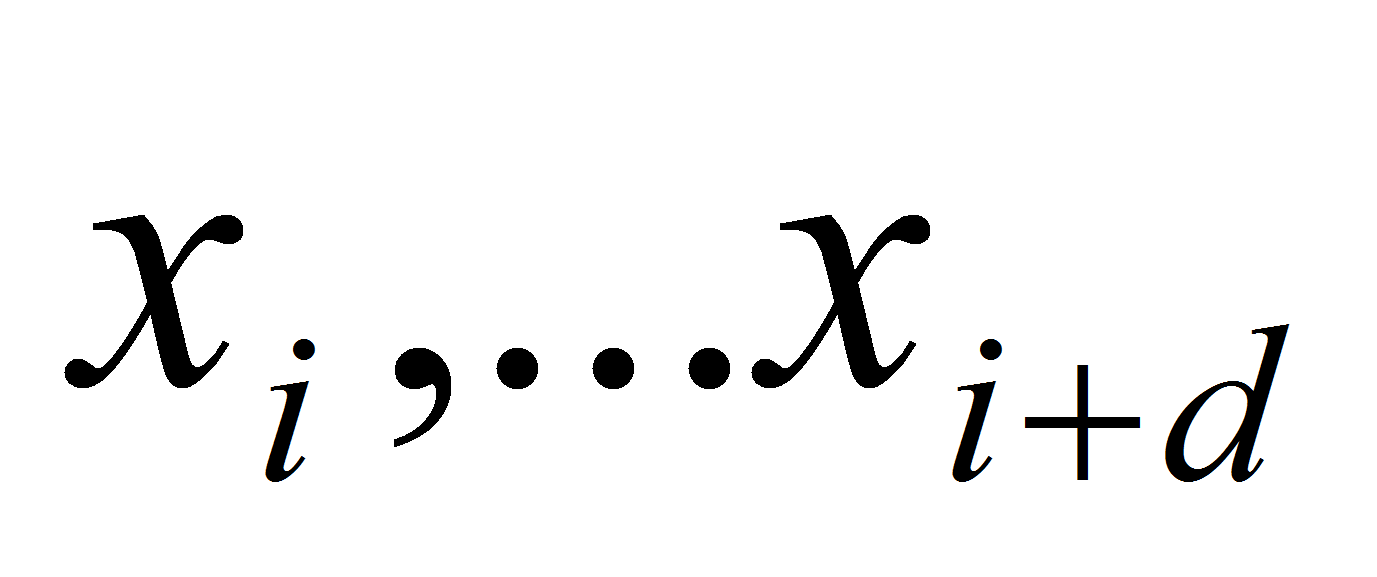 .
Тогда рациональный интерполянт Флоатера-Хорманна можно найти,
используя формулы:
.
Тогда рациональный интерполянт Флоатера-Хорманна можно найти,
используя формулы:
-
Интерполяция сплайнами [6]. Одним из недостатков
интерполирования многочленом Лагранжа или Ньютона на некотором
отрезке
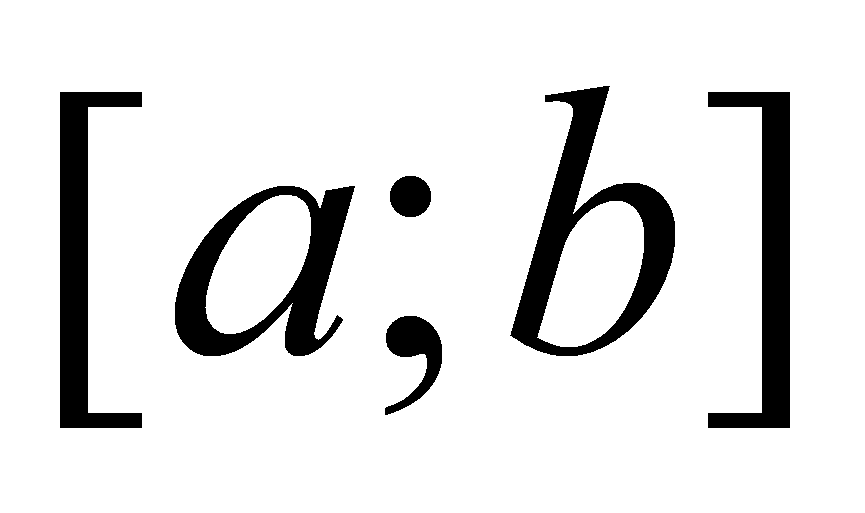 с использованием большого количества узлов интерполяции является
плохое приближение, вызванное сильным накоплением погрешностей в
процессе вычислений. Кроме того, не всегда увеличение числа приводит
к повышению точности вследствие расходимости процесса. Чтобы
избежать больших погрешностей весь отрезок
с использованием большого количества узлов интерполяции является
плохое приближение, вызванное сильным накоплением погрешностей в
процессе вычислений. Кроме того, не всегда увеличение числа приводит
к повышению точности вследствие расходимости процесса. Чтобы
избежать больших погрешностей весь отрезок
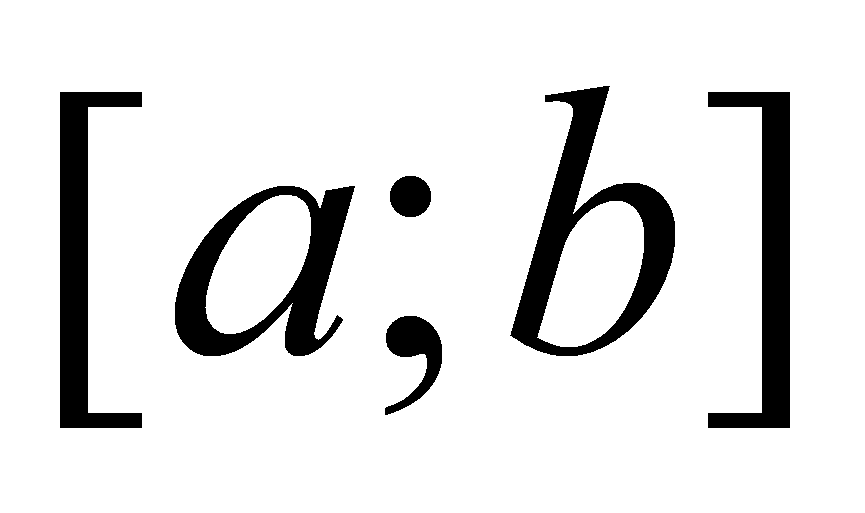 следует разбить на частичные отрезки и на каждом отрезке заменить
функцию
следует разбить на частичные отрезки и на каждом отрезке заменить
функцию
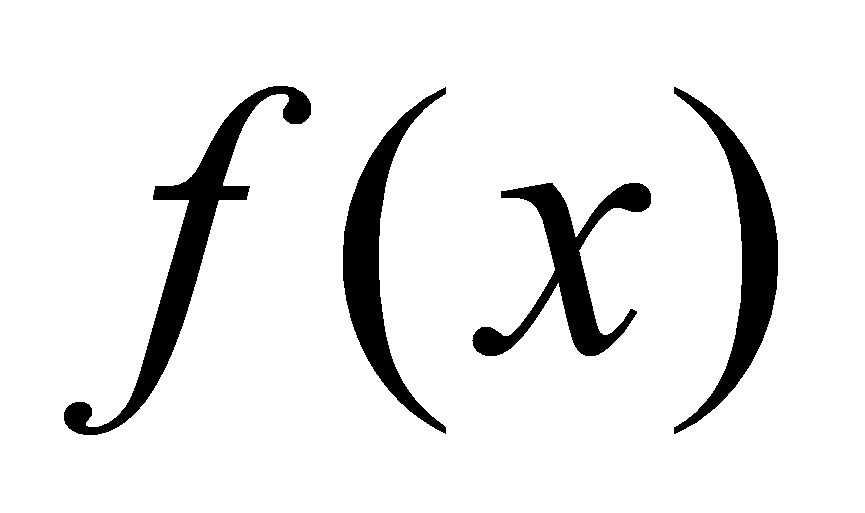 многочленом невысокой степени. Одним из способов интерполирования на
всем отрезке является интерполирование с помощью сплайн-функций.
Рассмотрим подробнее построение кубического сплайна.
многочленом невысокой степени. Одним из способов интерполирования на
всем отрезке является интерполирование с помощью сплайн-функций.
Рассмотрим подробнее построение кубического сплайна.
- Итак, на отрезке
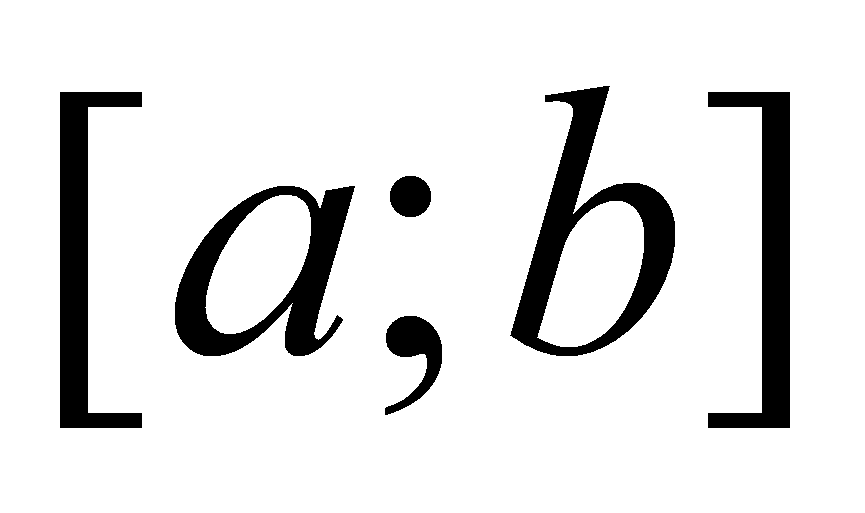 задана непрерывная функция
задана непрерывная функция
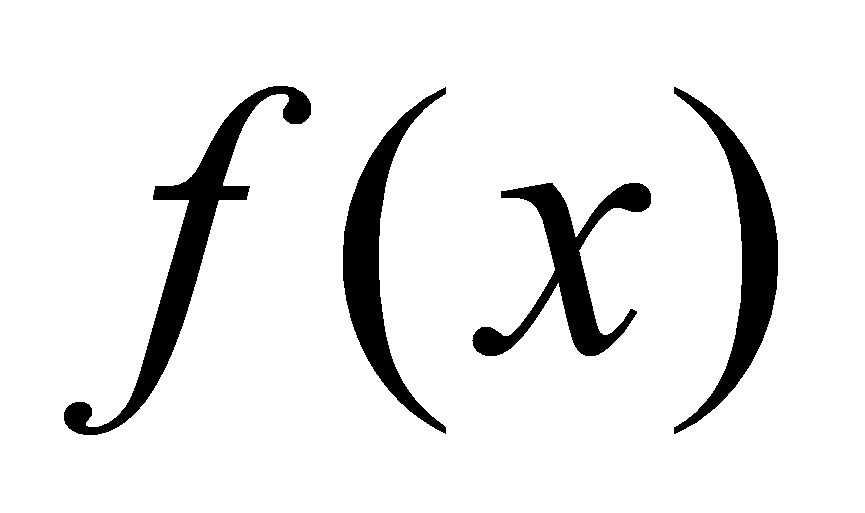 ,
некоторые точки сетки
,
некоторые точки сетки
 и значения функции
и значения функции
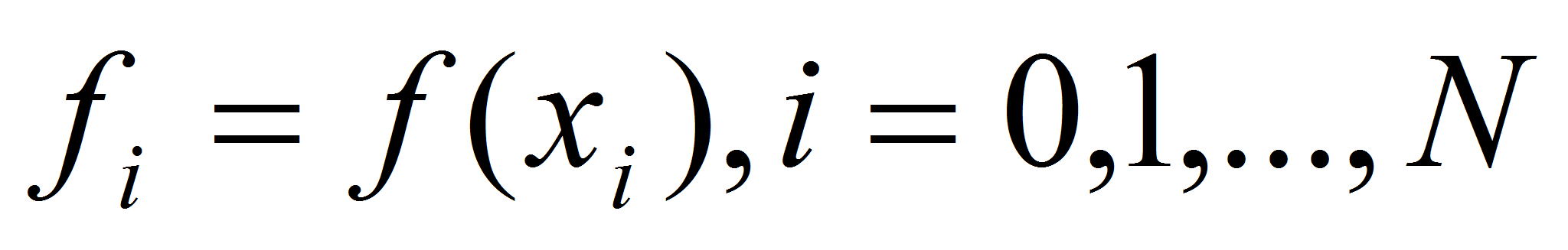 .
Интерполяционный кубический сплайн, соответствующий данной функции
.
Интерполяционный кубический сплайн, соответствующий данной функции
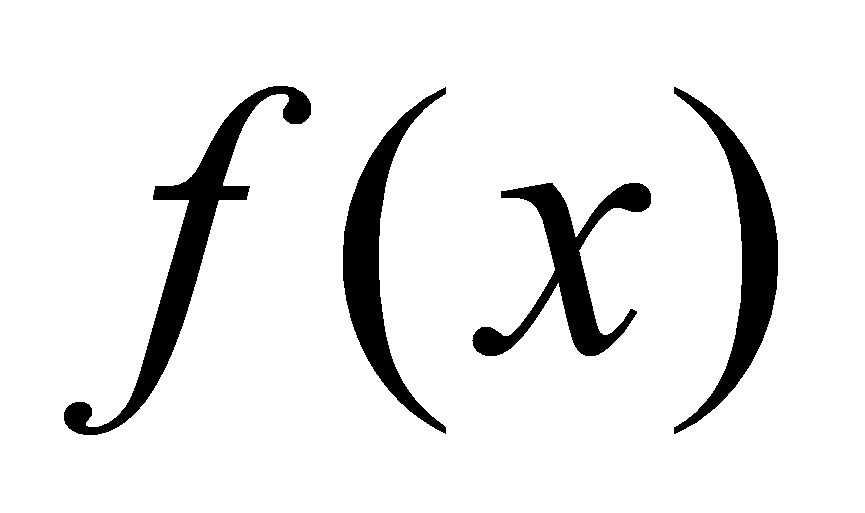 и данным узлам
и данным узлам
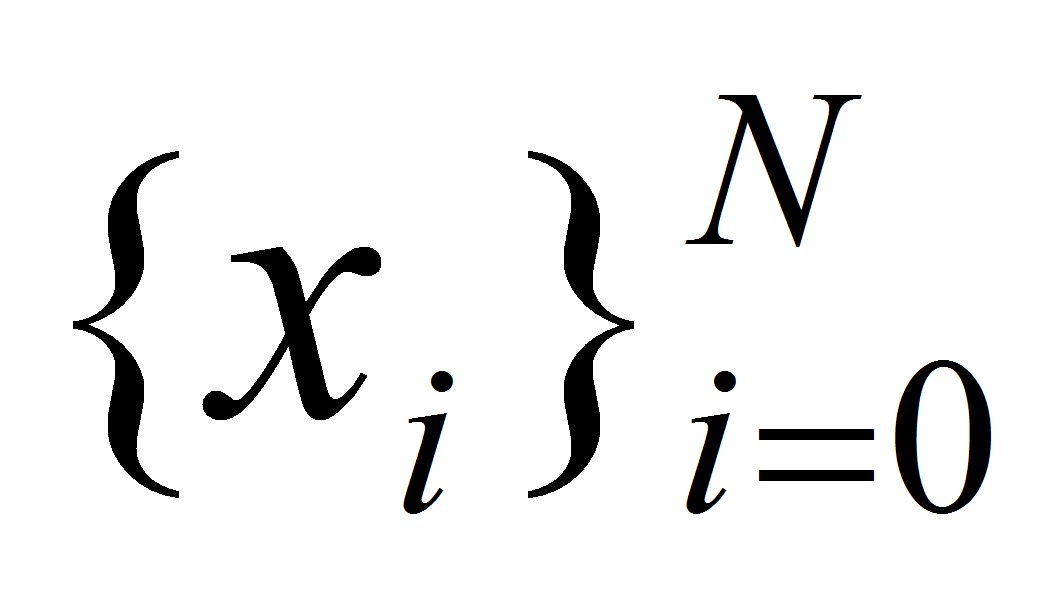 ,
- это функция
,
- это функция
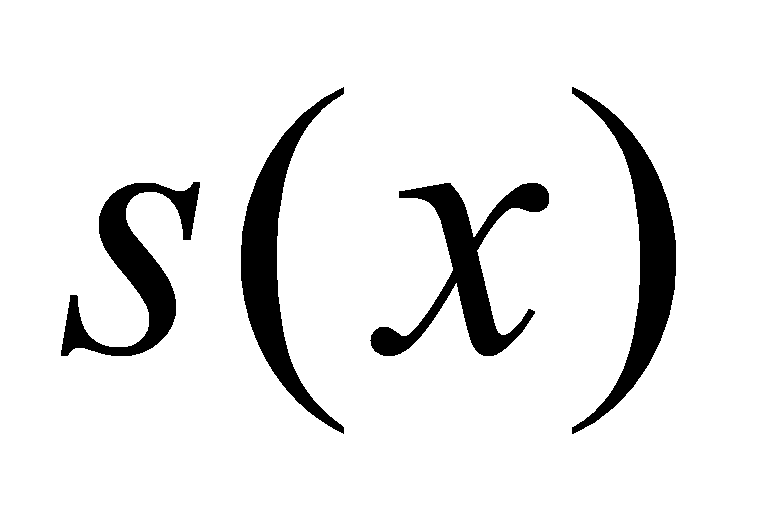 ,
удовлетворяющая следующим условиям:
,
удовлетворяющая следующим условиям:
-
на каждом сегменте
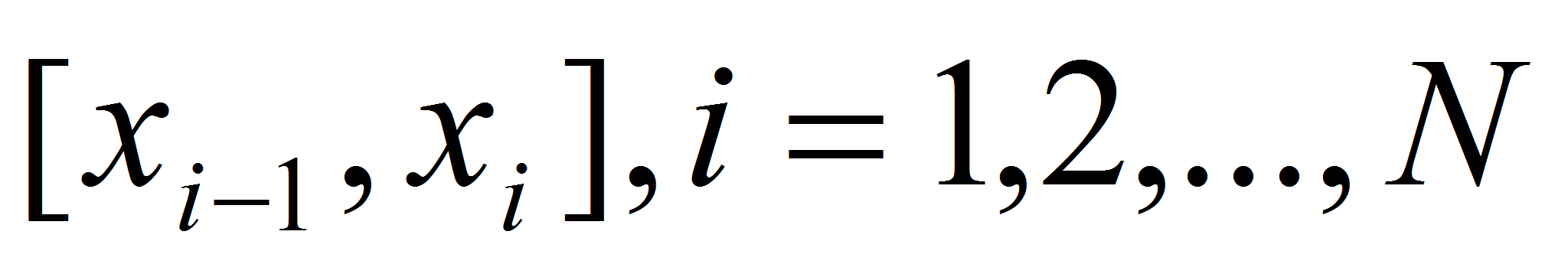 ,
функция
,
функция
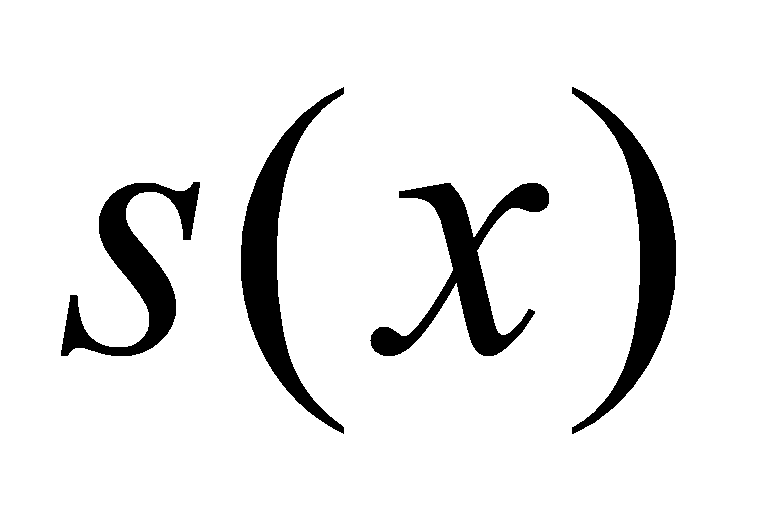 является многочленом третьей степени;
является многочленом третьей степени; -
функция
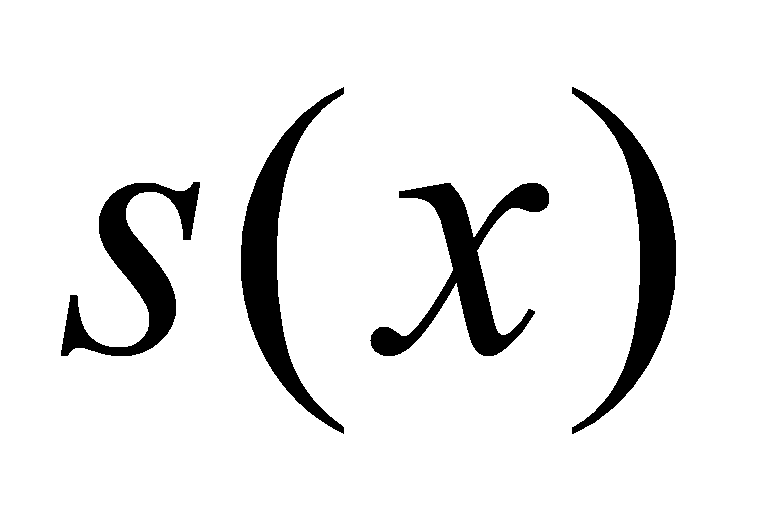 и ее первая и вторая производные непрерывны на
и ее первая и вторая производные непрерывны на
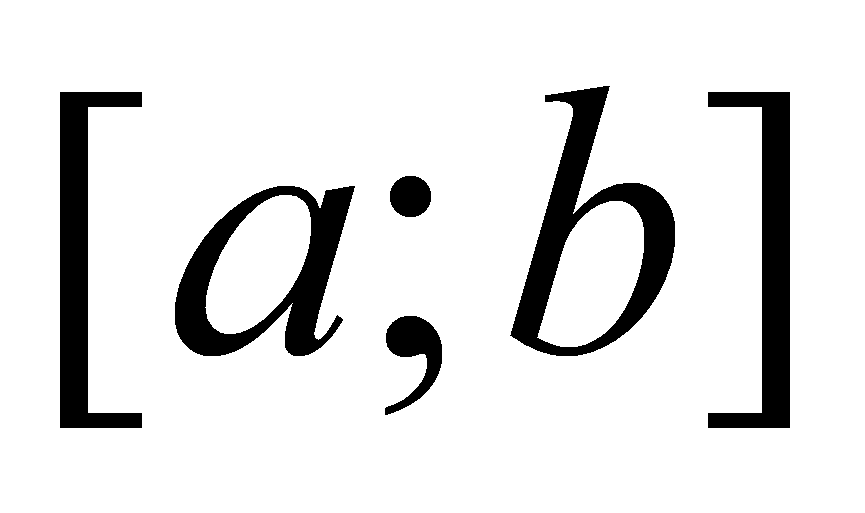 ;
; -
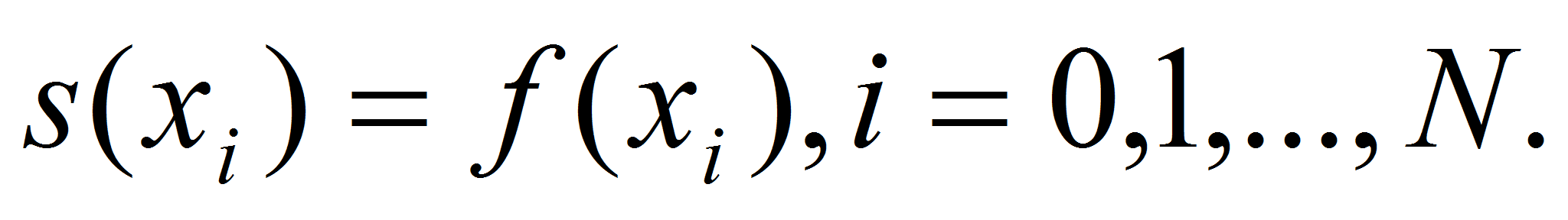
- Такой сплайн существует и является единственным
[6]. Рассмотрим способ построения кубического сплайна. На каждом из
отрезков
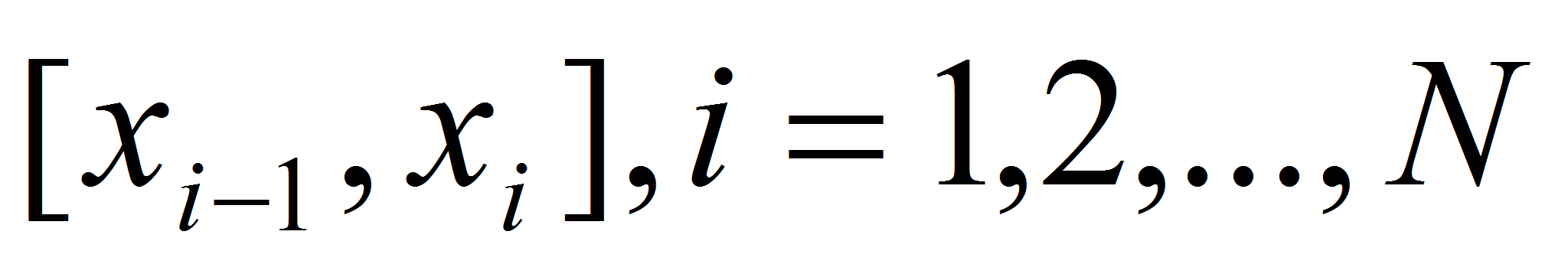 будем
искать функцию
будем
искать функцию
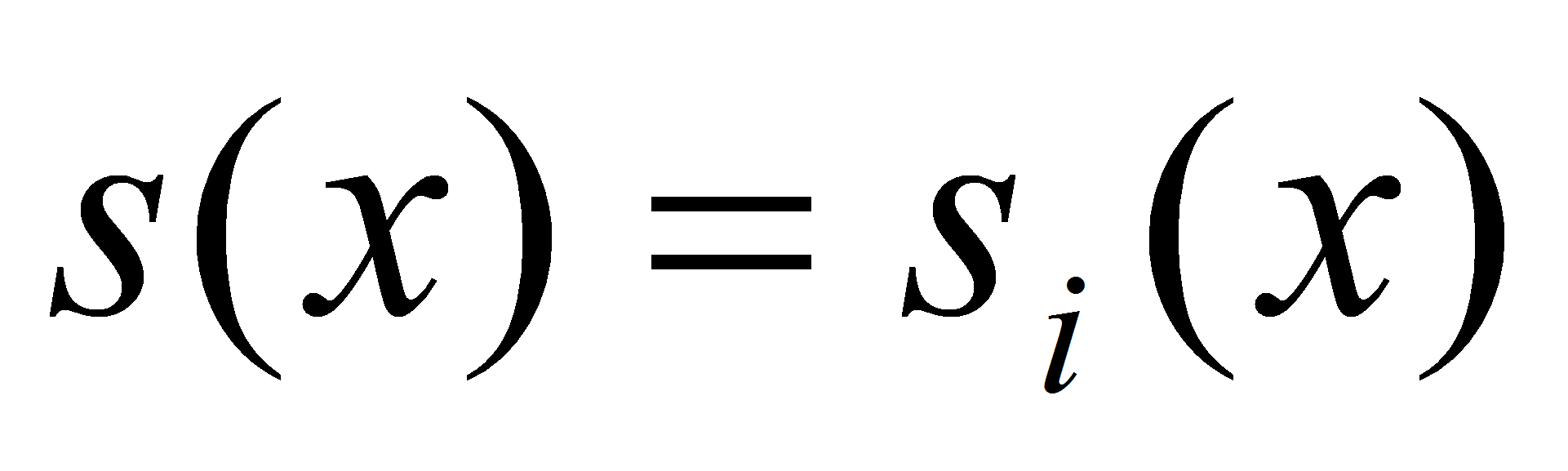 в виде многочлена третьей степени:
в виде многочлена третьей степени:
-
Здесь
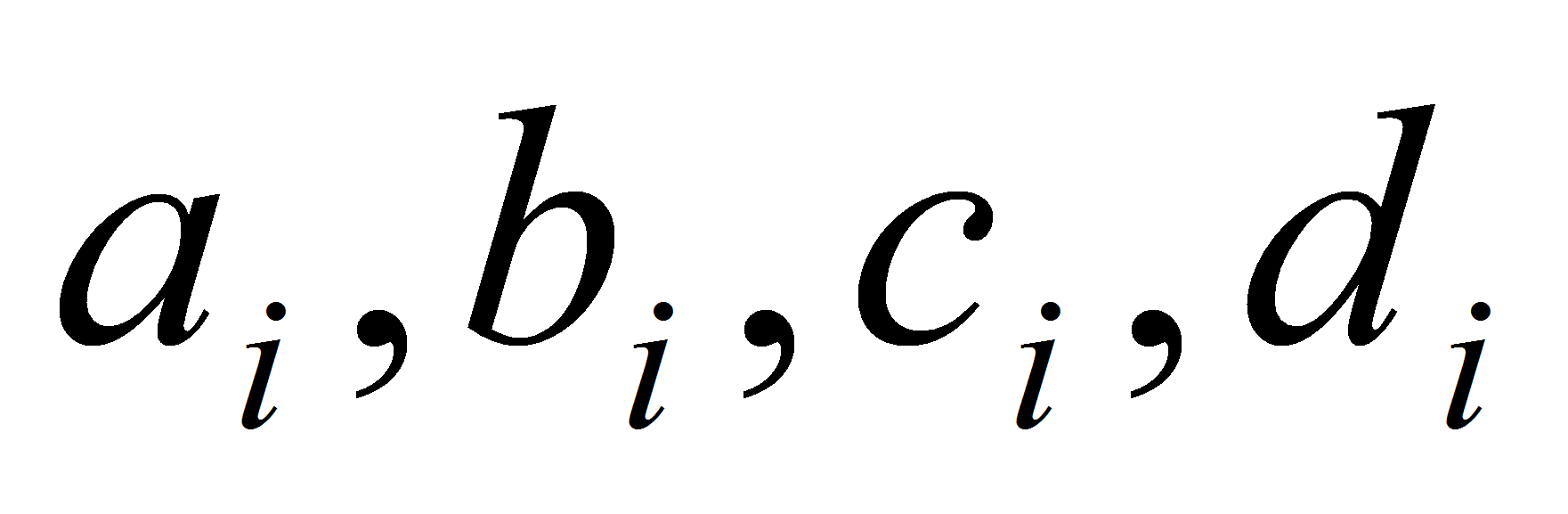 - это коэффициенты, которые необходимо найти. Отметим, что
- это коэффициенты, которые необходимо найти. Отметим, что
 .
Из условий интерполирования получаем:
.
Из условий интерполирования получаем:
- В результате получим кубический сплайн, удовлетворяющий условиям интерполяции. Этот сплайн является единственным [6].
- Разумеется, в данной статье приведены не все методы и способы интерполяции, например, тригонометрическая интерполяция, дробно-линейная интерполяция. Их описание можно найти в [6]. Однако, для решения задачи прогнозирования на архиве достаточно этих методов. Также можно произвести экстраполяцию несколькими разными методами и найти усредненное значение.
- Таким образом, применяя данные методы при использовании документов электронного архива, можно предсказать значения нужных аналитику атрибутов. Графическая реализация экстраполяции позволит наглядно понять имеющиеся тенденции развития организации.
- Литература:
- Кроль Т.Я. Схема наполнения электронного архива документами / Т.Я.Кроль, М.А.Харин, П.В.Евдокимов // Материалы первой международной конференции «Автоматизация управления и интеллектуальные системы и среды». Терскол, 20-27 дек. 2010. Т. IV. С. 53-56.
- Кроль Т.Я. Методы создания справочника на основе электронного архива / Т.Я. Кроль, М.А.Харин, П.В.Евдокимов // Известия КБНЦ РАН. – 2011. – №1.
- Сальвадори М.Дж. Численные методы в технике / М.Дж.Сальвадори. – М.: Издательство иностранной литературы, 1955. – 251с.
- Ващенко Г.В. Вычислительная математика: основы алгебраической и тригонометрической интерполяции / Г.В. Ващенко.- Красноярск: СибГТУ, 2008. – 64с.
- Бочканов С. Рациональная интерполяция [Электронный ресурс] / С. Бочканов, В.Быстрицкий. – Режим доступа: http://alglib.sources.ru/interpolation/rational.php, свободный.
- Самарский А.А. Численные методы: Учеб. пособие для вузов / А.А.Самарский, А.В.Гулин. – М.: Наука. Гл. ред. физ-мат. лит., 1989. – 432с.