Контроль качества промысловой отчетности на основе сравнения прогностического и фактического значений улова



Статья посвящена оценке качества промысловой отчетности в промышленном рыболовстве на основе прогностической модели процесса вылова рыбы. Оценка основана на сравнении прогностического значения улова и фактических данных промыслового отчета. Применение математической модели позволяет значительно уменьшить вычисляемый доверительный интервал ошибок отчетности и проводить эффективный контроль качества поступающих отчетных данных о вылове. Использование рекуррентных формул фильтра Калмана дает возможность реализовать вычисления в реальном масштабе времени. В совокупности, применение данного подхода обеспечит пользователей информационной рыбопромысловой системы качественной аналитической информацией.

Ключевые слова: информационная рыбопромысловая система, промысловая отчетность, авторегрессионная модель, фильтр Калмана, численные эксперименты.

ВВЕДЕНИЕ

Отраслевая система мониторинга (ОСМ) предназначена для мониторинга водных биологических ресурсов на основе постоянного наблюдения и контроля за выловом, транспортировкой и переработкой рыбы и морепродуктов [1, 2]. Решение такой комплексной задачи обеспечивается путем наблюдения за промысловой деятельностью на судах и рыболовных участках, местоположением судов и получения на этой основе косвенных показателей состояния водных биоресурсов: вылов на усилие и площади промысловых скоплений. Таким образом, все эти показатели, в виду оцениваемых факторов как поступающих оперативно, так и накопленных за предыдущие периоды промысла, позволяют оперативно отслеживать реализацию выделенных квот вылова, интенсивность промысла и его влияние на состояние рыбных запасов.

МАТЕРИАЛЫ И МЕТОДЫ

Конечной целью функционирования ОСМ является сохранение и контроль численности биоресурсов в размерах, необходимых для их воспроизводства и последующего использования в течение длительного срока. Используя как информационную основу поступающие в ОСМ сведения, формируются выходные формы, графики и другие аналитические материалы, позволяющие решать широкий спектр задач по управлению рыболовством, в том числе осуществлять контроль за местонахождением и деятельностью судов по добычи ими биоресурсов, следить за полнотой и достоверностью промысловой отчетности, поступающей от рыболовных участков и судов.

Информация ОСМ является источником для органов рыбоохраны, в задачи которых входят обязанности по проверке достоверности и правильности ведения отчетности, а также контроль соответствия результатов промысловой деятельности выделенным квотам. Основными данными для анализа в ОСМ являются результаты промысловых операций, выраженные в объемах выловленной рыбы — отчеты, ежесуточно передающиеся с промысловых судов и рыболовных участков. Источником этих сведений является промысловый журнал, который ведется на судне или участке. Помимо сведений о суточном улове и количестве рыбы, отгруженной по квитанции на транспорт или завод для дальнейшей обработки, в журнал заносятся более подробные сведения о промысловых операциях с указанием времени начала и окончания, её результатах, орудиях лова и прочем.

Процесс обработки входных данных ОСМ, после их поступления в центр мониторинга, включает в себя первичную обработку, в ходе которой формат исходных данных преобразуется во внутренний формат информационной системы, комплексный анализ, который выполняет синтаксические и семантический анализ данных и подготовка аналитического материала, внесение в базу данных, отправка информации другим пользователям [3]. Проверка данных, поступающих в OCM, необходима, поскольку есть ошибки случайного и преднамеренного характера, когда пользователь ВБР хочет скрыть реальную величину улова. Несмотря на то, что в большинстве случаев ошибки носят непреднамеренный характер, факты браконьерства на промысле все же имеют место.

Контроль количества улова [4] — сложная задача, т. к. размер улова зависит от многих факторов: состояния сырьевой базы, погодных условий, технологических особенностей судна или участка добычи и может варьироваться от нуля до максимума в производственном смысле (т. е. зависит от производительности оборудования для обработки сырья). Поэтому для указанного в отчете количества улова устанавливается доверительный интервал, в который с большой вероятностью должен соответствовать размер улова. В целом, как упоминалось выше, доверительный интервал включает все возможные значения вылова.

Предлагается уменьшить доверительный интервал, используя математическую модель для расчета значения вылова за отчетный день, т. е. прогнозируя значение вылова по времени на один шаг вперед после даты предыдущего отчета. Этот прогнозируемый улов сравнивается с зарегистрированным уловом. Условием удовлетворительного качества полученного отчета в данном случае является то, что сообщаемое значение попадает в доверительный интервал прогноза. Предполагается, что можно построить модель, в которой дисперсия ошибки прогноза будет меньше дисперсии самого процесса, и поэтому доверительный интервал обеспечит эффективный контроль сообщаемых данных. Также можно уменьшить доверительный интервал, включив в модель отчеты с ближайших судов и районов промысла, чтобы картина изменений промысловой ситуации имела очевидную пространственную корреляцию.

В ОСМ есть тысячи судов и рыболовных угодий, и ясно, что нужно построить тысячи моделей. Так как объекты отчетности отличаются друг от друга, что является непростой задачей в вычислительном отношении, поэтому для расчета параметров математической модели будут использованы эффективные алгоритмы.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Отчетную величину улова на участке – за указанные сутки можно рассматривать как сумму двух элементов: первой части, являющейся функцией всех значений до выбранных суток , и случайной составляющей [5]:

(1)

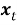
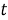
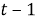
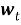
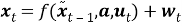
В этом уравнении – это совокупность данных вектора

, полученных до настоящего момента времени, то есть ; – вектор неизвестных коэффициентов модели; – управляющее воздействие, либо экзогенный фактор; – последовательность независимых одинаково распределенных величин; – детерминированная функция.

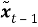
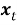
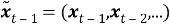
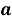
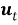
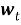
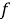
Ввод в уравнение шума отражает допущенные погрешности при случайном или умышленном искажении величины улова, а также поиске неизвестного вида функции .

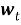
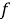
Если привести уравнение (1) в векторно-матричный вид, то система уравнений для m-мерного векторного процесса

будет выглядеть следующим образом:

(2)

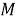
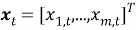
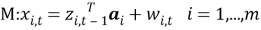
где - мерный вектор;

– n ₀ -мерный вектор ;

– случайные гауссовы возмущения типа «белого шума»;

– имеет размерность и составляется в виде функции из компонент векторов ;

– наблюдаемый входной вектор.

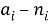
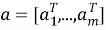
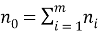
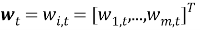
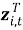
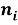
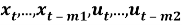
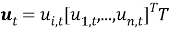
Класс многомерных динамических моделей представляется тройкой: ( ), где – уравнение (2), содержащее -мерный вектор ; – множество всех значений, которые может принимать вектор

; – множество всех положительно определенных матриц шума .

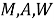
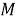
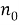
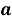
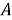
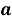
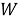
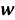
Если предположить, что к моменту времени накоплена совокупность наблюдений процессов и :

(3)

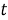
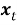
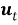
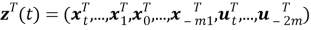
То, исходя из вектора наблюдений и заданного критерия, потребуется найти оценки параметров: вектора

и матрицы ,. Поскольку на практике необходимо еще и учитывать случайные отклонения, логичным будет ввести в правую часть уравнения (3) шум , чтобы компенсировать недостатки модели. Естественно, за счет подбора вида функции и вектора коэффициентов модели , возможно минимизировать влияние шума:

(4)

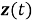
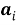
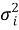
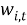
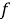
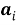
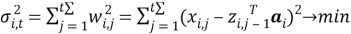
При этом минимизация (4) для вектора даст выражение в виде:

(5)

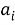
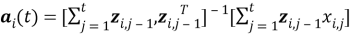
Отсюда можно сделать вывод, что вектор коэффициентов модели для уравнения рассчитывается без учета остальных уравнений. Для математического ожидания и дисперсии справедливо следующее:

(6)

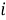
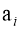
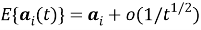
В ряде случаев, когда и статистически независимы, оценка квазимаксимального правдоподобия совпадает с оценкой условного максимального правдоподобия, а значит является состоятельной и асимптотически несмещенной. Оценка на основе ограниченной информации является состоятельной, но не всегда эффективной (см. работы [6-10]).

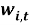
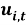
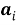
Важное преимущество метода оценивания на основе ограниченной информации состоит в том, что он позволяет находить состоятельную оценку даже в условиях отсутствия знания

. Данный метод позволяет осуществлять декомпозицию задачи оценивания на ряд автономных задач оценивания для отдельных уравнений системы, что существенно упрощает задачу в вычислительном аспекте.

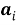
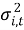
Расчет по формуле (5) требует необходимости запоминания всей совокупности наблюдений до момента времени . При мониторинге, т.е. непрерывном отслеживании динамики показателей, характеризующих процесс, необходим пересчет оценки в новые оценки с использованием данных новейших наблюдений . Проведение подобных расчетов требует выполнения растущего с числом количества суммирований, что закономерно приведет к росту затрат на поиск и отбор записей наблюдений при реализации на ЭВМ.

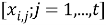
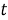
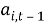
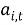
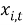
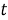
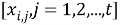
Для решения это проблемы можно воспользоваться алгоритмом, принадлежащим семейству алгоритмов фильтрации Калмана и реализующем процедуру вычислений оценки коэффициентов модели в реальном масштабе времени. Суть алгоритма, реализующего Калмановскую фильтрацию, заключается в согласовании наблюдений и физических моделей.

Если ввести в рассмотрение матрицу

:

(7)

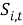
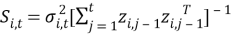
Оценку вектора коэффициентов модели при этом можно записать в виде:

(8)

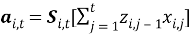
При этом алгоритм вычисления оценки , исходя из описанных соотношений, представится в следующем виде:

(9)

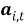
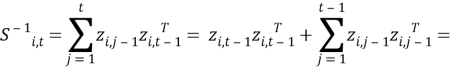
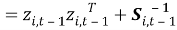
Из этого выражения можно получить соотношение:

(10)

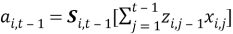
Тогда выражение для в конечном итоге будет выглядеть следующим образом:

(11)

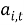
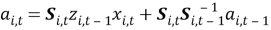
Алгоритм управления входными отчетными данными следующий: модель для конкретного промыслового участка используется при прогнозировании на один шаг вперед во времени и сравнения этого значения с отчетом об улове, полученным на эту дату. Если расхождение укладывается в доверительный интервал, то полученный отчет, скорее всего, надежен и нет оснований подозревать пользователя ВБР в его искажении. Если расхождение велико, то это прямой сигнал для анализа полученных данных на предмет их ошибочности или преднамеренного искажения. После исправления ошибок отчета коэффициенты модели и матрица ковариации ошибок пересчитываются и сохраняются в базе данных.

ЗАКЛЮЧЕНИЕ

Применение математической модели рыбопромыслового участка позволит значительно улучшить проводимый контроль качества поступающих с рыболовных участков отчетных данных о вылове. В виду того, что количество участков, как и количество соответствующих им моделей велико, применение рекуррентных формул фильтра Калмана весьма целесообразно. В совокупности, повышение качества промысловой информации ОСМ поспособствует обеспечению пользователей системы качественной аналитической информацией, что приведет к росту эффективности управления и позволит выявить ключевые направления для дальнейшего развития этого сегмента отрасли.

Литература:

1. Кошкарева Л. А. Алгоритм контроля расхода сырца при выпуске рыбной продукции на основе данных промысловой отчетности // Материалы международных научных чтений «Приморские зори — 2005». Владивосток: ТАНЭБ, 2005. — 286 с. Выпуск второй.
2. Мониторинг рыболовства 2005. Инструкции и рекомендации экипажам промысловых судов и судовладельцам. Под общ. ред. д.т.н. Проценко И. Г., — Петропавловск-Камч.: ФГУП «Камчатский центр связи и мониторинга», 2005. — 264с.
3. Проценко И. Г. Оптимизация обработки входной информации в отраслевой системе мониторинга рыболовства // Международный научно-исследовательский журнал, № 8(86)/2019.Часть 1,Август,Екатеринбург, ISSN 2227–6017 (ONLINE), ISSN 2303–9868 (PRINT), DOI:10.18454/IRJ.2227–6017.ПИ № ФС 77–51217,16+
4. Проценко И. Г. Информационная система мониторинга рыболовства // Рыбное хозяйство, 2001. Спец. выпуск. С.3–18.
5. Кашьяп Р. Л., Рао.А. Р. Построение динамических стохастических моделей по экспериментальным данным // Пер. с англ.,- М.: Наука, 1983.
6. Браммер К., Зиффлинг Г. Фильтр Калмана-Бьюси. // М.: Наука, 1982. [Электронный ресурс] — Режим доступа: https://www.twirpx.com/file/21556/
7. Калман Р. Л., Фалб., Арбиб М. Очерки по математической теории систем. М.: Мир, 1971.
8. Эпстейн Эд. С. Стохастические динамические предикаты. -Теллус, гл.21, с.739–759, 1969.
9. Калман Р. Э. Новые методы в теории Винеровской фильтрации. -В: Proc.Symp.Eng.Appl.Random Functious — Нью-Йорк: Wiley, 1963.
10. Петерсен Д. П. О концепции и реализации последовательного анализа для линейных случайных полей.- Теллис, т. 20, № 4, с. 673–686, 1968.