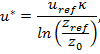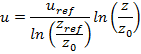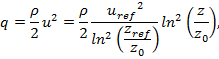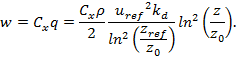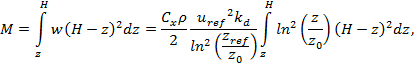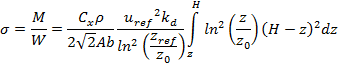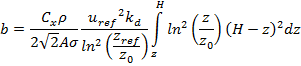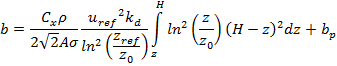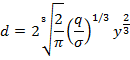1. Введение
При проектировании современных башен связи особое значение приобретает выбор таких конструктивных и архитектурных решений, при которых конструкция будет иметь минимальный расход строительных материалов при обеспечении условий функциональности, равнопрочности и равноресурсности ее элементов. В настоящей работе приводятся результаты исследования одного из принципов пространственной конфигурации башни связи, использованного при проектировании сооружений в интересах компаний-операторов. Кроме того, исследованы экономические аспекты разработанных конструкций, которые проиллюстрированы на одном из конкретных примеров.
2. Методика
На сегодняшний день известен и получил широкое распространение ряд конструкций ферменных башен связи:
1. Башни с прямоугольным стволом, в которых ширина является постоянна по высоте.
Достоинством таких башен является компактность расположения. Недостатки: малый угол опрокидывания и, соответственно, низкий запас устойчивости от опрокидывания, большие нагрузки на основание, повышенный расход металла, требуемый для выполнений предельных состояний первого и второго рода.
Примеры башен: башня ООО Строймонтажинвест в селе Цугол Иркутской области, башня ООО «Усть-Илимскэнергопроект» в г. Братск.
2. Башни трапециевидной формы, в которых ширина уменьшается с ростом высоты по линейному закону.
Достоинства – большие значения угла опрокидывания, меньшие нагрузки на основание. Недостаток – неравнопрочность и неравноресурсность элементов башни и, как следствие, повышенный расход строительных материалов.
Примеры башен: башня в селе Усть-Алтан Иркутской области, антенные опоры НИИ Энергосетьпроект.
3. Башни переменной ширины, в которых ширина зависит от высоты по определенному закону, например, близкому к закону распределения изгибающих моментов по высоте. Закон распределения изгибающих моментов по высоте определяют либо эмпирическим путем, либо с использованием нормативных документов. К примеру, в настоящее время в России применяется свод правил СП20.13330.2011 (актуализированная редакция строительных норм и правил СНиП 2.01.07-85*).
Примеры построенных башен: Эйфелева башня в Париже, башня ООО Проектно-строительное бюро в селе Колобки Республики Бурятия, башня компании Астеко тип «Рязань» и многие другие.
Достоинства – такие башни имеют большую степень равнопрочности и равноресурсности. Недостатки – отличие принимаемых в расчетах законов распределения изгибающих моментов по высоте от реальных и неучет динамической составляющей ветровой нагрузки не позволяет достигнуть больших значений равнопрочности и равноресурсности элементов башни, а также меньших значений расхода строительных материалов.
Исследуемое в данной работе техническое решение направлено на устранение недостатков таких башен за счет применения нового правила создания формы башни, т.е. закона изменения ширины башни по высоте. При этом в основе данного правила лежит вертикальный профиль скоростей ветра по логарифмической модели Монина-Обухова при условии нейтральной стратификации. Ниже приводится пример построения профиля башни с использованием предлагаемого правила.
Профиль башни определяется из условия равнопрочности стоек фермы. В целях оптимизации рассматривается нагружение фермы только ветровой нагрузкой, поскольку ветровые нагрузки являются доминирующими для данного типа сооружений. В данном примере не учитывается наличие навесных элементов на башне, хотя в общем правиле такой учет может иметь место.
Нагружение стоек башни происходит главным образом за счет изгибающих моментов, поэтому действием поперечных сил пренебрегаем. Вертикальный профиль скорости по логарифмической модели Монина-Обухова, при нейтральной стратификации,
где
![]() – постоянна Кармана (
– постоянна Кармана (![]() );
z
– текущая высота; z0
– параметр шероховатости.
);
z
– текущая высота; z0
– параметр шероховатости.
- Скорость
где
![]() – скорость ветра на высоте
– скорость ветра на высоте
![]() ,
которая может быть получена путем фактических измерений.
,
которая может быть получена путем фактических измерений.
- Таким образом, профиль скоростей задается соотношением
- Скоростной напор
где
![]() - плотность воздуха, которая в данном примере полагается постоянной
по высоте.
- плотность воздуха, которая в данном примере полагается постоянной
по высоте.
Связь
между величинами давлений постоянной составляющей ветровой нагрузки
(![]() )
и суммарной (
)
и суммарной (![]() ),
включающей пульсационную составляющую, можно записать следующим
образом
),
включающей пульсационную составляющую, можно записать следующим
образом
Поскольку скорости ветра пропорциональны давлениям, то соотношение между постоянной и суммарной расчетной скоростями имеет вид
- Тогда расчетное давление
Здесь эквивалентный коэффициент сопротивления с учетом затенения и направления ветра
где
![]() – площадь контура башни;
– площадь контура башни;
![]() – коэффициент аэродинамического сопротивления i-го
элемента фермы;
– коэффициент аэродинамического сопротивления i-го
элемента фермы;
![]() – площадь миделевого сечения i-го
элемента фермы.
– площадь миделевого сечения i-го
элемента фермы.
где
![]() – коэффициент заполнения фермы (отношение суммы площадей
миделевых сечений балок к площади контура башни), b
– ширина на уровне h.
– коэффициент заполнения фермы (отношение суммы площадей
миделевых сечений балок к площади контура башни), b
– ширина на уровне h.
-
Для
четырехгранной башни, при
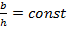
-
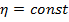
-
Коэффициент,
учитывающий направления ветра
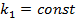 .
. -
Принимая
в данном примере для профилей осредненной значение
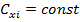 ,
имеем
,
имеем
где H – высота башни, dz – приращение высоты.
Местный момент инерции для четырехгранной башни (не учитывая внутренние элементы решетки ) при нагрузке в плоскости диагонали
- где A – площадь поперечного сечения стойки.
- Местный момент сопротивления
Видно, что при z = H b = 0, что непрактично, поскольку в верхней части башня должна иметь определенную ширину по технологическим соображениям, обозначенную bp. В этом случае закон распределения ширин по высоте записывается в виде
Анализируя полученную зависимость, можно заметить, что из-за требования к ненулевой ширине в верхней части башни, равнонагруженность стоек несколько нарушается, поскольку в верхней части, где изгибающие моменты малы или близки к нулю, момент сопротивления имеет конечную, как правило, довольно значительную, величину. В результате, чтобы избежать чрезмерных запасов прочности, стойки верхней части башни должны иметь профили с меньшей площадью поперечного сечения.
Ниже приведена совокупность признаков, отличающих исследованный принцип пространственной конфигурации: башня связи,
- выполненная в виде пространственной трехгранной, четырехгранной или многогранной вертикальной ферменной металлической конструкции,
- теоретическая конфигурация которой – зависимость ширины от высоты определяется в соответствии с эпюрой изгибающих моментов от поперечных сил, действующих в направлении, перпендикулярных вертикальной оси башни,
- в которой теоретическая конфигурация – зависимость ширины от высоты, описываемая непрерывной кривой, – заменяется ломаной кривой, состоящей из нескольких прямых, причем в верхней части часть башни имеет постоянную ширину,
- в которой эпюра изгибающих моментов определяется с учетом аналитической зависимости ветровой нагрузки на ферму от высоты, а также сил аэродинамического сопротивления навешиваемых на башню антенн и прочего технологического оборудования,
- в которой аналитическая зависимость ветровой нагрузки от высоты определяется в зависимости от теоретического распределения скоростей ветра по высоте,
- в которой учитывается динамическая составляющая ветровой нагрузки,
- в которой в качестве теоретического распределения скоростей ветра по высоте определяется в соответствии с моделью Монина-Обухова при условии нейтральной стратификации,
- ширина основания которой задается в зависимости от требуемых величин давления на основание, отрывных нагрузок, угла опрокидывания, а также технологических требований,
- ширина верхней части с постоянной шириной которой определяется технологическими и эксплуатационным и требованиями,
- элементы фермы которой выполняются в виде труб или профилей (уголков, швеллеров, парных уголков, тавров, двутавров, квадратов, прямоугольников, труб коробчатого сечения), соединяемых между собой посредством сварки, болтовых, заклепочных соединений, через фасонки или непосредственно,
- стойки которых выполняются в виде неразрезных непрерывающихся в узлах балок,
- размеры поперечных сечений элементов фермы которой выбираются из условия обеспечения первого (прочность, устойчивость) и второго (деформации) предельного состояний при действии нормированных ветровых, снеговых, гололедных, сейсмических нагрузок и веса,
- в которой могут быть установлены горизонтальные диагональные связи, соединяющие стойки, не принадлежащие одной грани.
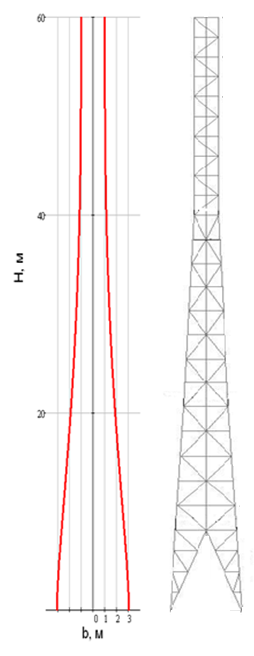
Рис.2.1
Технический эффект – равнопрочная равноресурсная конструкция, сниженный расход строительных материалов.
На рис.2.1 показан профиль башни высотой 60 м, построенный с применением предлагаемого правила. Был также разработан ряд конструкций башен связи для использования телекоммуникационными компаниями в диапазоне высот от 30 до 75 метров.
Проверка каждой из башен на предельные состояния первого (прочность, устойчивость) и второго (деформативность) рода осуществлена с использованием современных технологий компьютерного моделирования, в том числе примененных для определения ветровых нагрузок (методы конечных элементов и контрольных объемов).
3. Экономические аспекты
В данном разделе исследуются соотношения между параметрами оптимальной конструкции и сравнительный анализ весового совершенства, а также производится оценка экономической выгоды использования уголковых профилей по сравнению с трубчатыми.
Для иллюстрации соотношений между массой, высотой и нагрузкой оптимальной башни, определим формулу, связывающие данные величины, для простоты, на примере балки круглого сечения диаметром d, переменного по высоте, имеющей общую высоту H, и нагруженную равномерно распределенной нагрузкой интенсивностью q.
Для башенных сооружений характерно преобладающее влияние изгибающих моментов, поэтому вкладом поперечных сил в напряженно-деформированное состояние можно пренебречь. В этом случае напряжения в балке определяться следующим образом
где M – изгибающий момент, W – момент сопротивления. Данные величины вычисляются в рассматриваемых условиях таким образом
где y – расстояние от вершины башни до рассматриваемого сечения.
Отсюда,
полагая
![]() ,
можно получить зависимость поперечного размера балки d
от уровня размещения y:
,
можно получить зависимость поперечного размера балки d
от уровня размещения y:
Площадь сечения на данном уровне
Объем балки
Масса балки
Таким образом, масса конструкции пропорциональна высоте в степени 7/3 и нагрузке в степени 2/3. При сравнении масс двух башен оптимальной конструкции (&#; = const), выполненных из одного материала полагаем, что уровень напряжений в них одинаков. Тогда
где
![]() – соотношение между действующими нагрузками; p2,
p1
– нормированные давления;
– соотношение между действующими нагрузками; p2,
p1
– нормированные давления;
![]() – соотношение между высотами конструкций.
– соотношение между высотами конструкций.
Коэффициент
![]() может служить для сравнительной оценки меры весового совершенства
конструкции.
может служить для сравнительной оценки меры весового совершенства
конструкции.
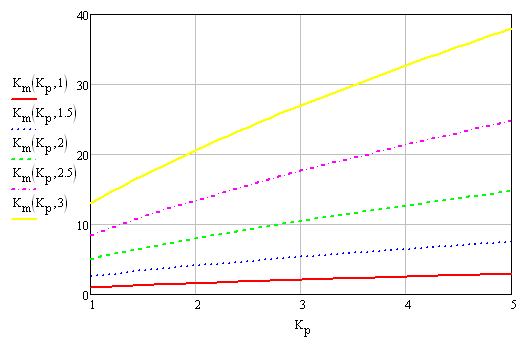
На
рис.3.1 показана зависимость коэффициента
![]() от коэффициента
от коэффициента
![]() при различных значениях коэффициента
при различных значениях коэффициента
![]() .
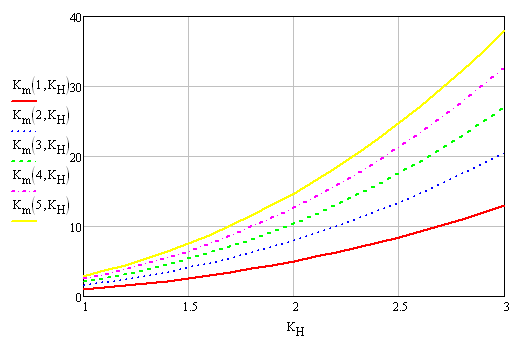
На рис.3.2 показана зависимость коэффициента
.
На рис.3.2 показана зависимость коэффициента
![]() от коэффициента
от коэффициента
![]() при различных значениях коэффициента
при различных значениях коэффициента
![]() .
.
Произведем сравнение между разрабатываемой уголковой башней высотой H2 = 52 м, спроектированной для третьего ветрового района (р2 = 380 Па), и уголковой башней ООО «Астеко» высотой H1 = 50 м, спроектированной для второго ветрового района (р1 = 300 Па), массой 19631 кг. В этом случае
Значит,
эквивалентная башня должна иметь массу
![]() Оцениваемая масса спроектированной конструкции составляет примерно
16.7 тонн, т.е. данная башня обладает большим весовым совершенством,
чем башня ООО
«Астеко» высотой 50 м.
Оцениваемая масса спроектированной конструкции составляет примерно
16.7 тонн, т.е. данная башня обладает большим весовым совершенством,
чем башня ООО
«Астеко» высотой 50 м.
Рис.3.1
Рис.3.2
Аналогичным образом произведем сравнение с другими уголковыми башнями ООО «Астеко». Результаты сведены в таблицу 3.1.
Таблица 3.1
|
Тип башни |
Нормативное давление, Па |
KH |
Kp |
Km |
Масса эквивалентной башни, кг |
Разница |
|
Н=64м.II в.р. тип «Рязань» |
300 |
0.813 |
1.267 |
0.721 |
16492 |
-1.1% |
|
Н=64м.II в.р. тип «Звезда» |
300 |
0.813 |
1.267 |
0.721 |
17195 |
3.1% |
|
Н=64м.III в.р. тип «Рязань» |
380 |
0.813 |
1.000 |
0.616 |
16336 |
-2.0% |
|
Н=64м.III в.р. тип «Звезда» |
380 |
0.813 |
1.000 |
0.616 |
16740 |
0.4% |
|
Н=50м . II в.р.(тип Звезда) |
300 |
1.040 |
1.267 |
1.283 |
25184 |
51.1% |
|
Н=40м . II в.р.(тип Рязань) |
300 |
1.300 |
1.267 |
2.159 |
36114 |
116.6% |
|
Н=44м . II в.р.(тип Звезда) |
300 |
1.182 |
1.267 |
1.729 |
28761 |
72.5% |
|
Н-70 м. II в.р. |
230 |
0.743 |
1.652 |
0.698 |
17842 |
7.0% |
|
Н-50м. I в.р. |
230 |
1.040 |
1.652 |
1.531 |
18168 |
9.0% |
Как следует из таблицы 3.1, оценка массы эквивалетной башни находится в пределах 16.3 – 36.1 тонн, со средним значением 21.4 тонны. Это свидетельствует о том, что башни спроектированы под широкую номенклатуру обвеса, причем башни большей массы предназначены для установки большего по размерам оборудования.
Исходя из данных таблицы 1 можно сделать вывод о том, что спроектированная башня по весовому совершенству близка к лучшим существующим башням. Учитывая то, что предлагаемая башня изначальна ориентирована на использование относительно большого состава навесного оборудования, и имеет резервы для дополнительной навески, можно заключить, что потенциально данная конструкция несколько лучше представленных на рынке.
Как известно, при использовании трубчатых балок существует возможность уменьшить вес конструкции башни за счет снижения нагрузок (аэродинамического сопротивления) и относительно большей прочности и устойчивости труб под нагрузкой. За это приходится платить усложнением технологии изготовления башни, а значит и приведенной стоимости конструкции.
По данным ООО «Астеко», стоимость одной тонны башни, выполненной из уголковых профилей, равна 60 тысячам рублей, в то время как тонна башни из труб стоит 75 тысяч рублей (на 25% дороже).
Для оценки возможной экономии массы при использовании труб вместо профилей воспользуемя данными по башням ООО «Астеко»:
- Уголковая башня высотой 44 м, спроектированная для второго ветрового района, массой 16637 кг.
- Трубчатая башня высотой 44.6 м, спроектированная для второго ветрового района, массой 13770 кг.
В первом случае для эквивалентной башни высотой 52 м в третьем ветровом районе получаем:
Во втором случае для эквивалентной башни получаем:
Полагая, что соотношение между массами уголковых и трубчатых башен неизменно, получаем оцениваемую экономию массы при использовании труб для спроектированной башни (с оцениваемой массой 16672 кг)
и новую массу башни
Оцениваемая стоимость уголковой башни
Оцениваемая стоимость
Таким образом, разница в стоимости между уголковой и трубчатой башней в рассматриваемых условиях незначительна, и даже, как видно в данном примере, уголковая башня может стоить дешевле трубчатой. Учитывая все эксплуатационные недостатки трубчатых башен (таких, например, как сложность контроля коррозии внутренних полостей и низкая компенсационная способность длины при сборке) следует сделать вывод, что применение башни, выполненной из уголков, является более выгодным.
-
- Литература:
- Свод правил СП20.13330.2011. Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07-85*. – М.: ОАО «ЦПП» 2011. – 81 с.
- Атмосфера. Справочник. – Л.: Гидрометеоиздат, 1991. – 510 с.
- Металлические конструкции / Под ред. Беленя Е.И. – М.: Стройиздат, 1986. – 560 с.
- Инженерные конструкции / Под. Ред. В.В. Ермолова. – М.: «Архитектура С», 2007. – 408 с.
- http://ooo-asteko.ru/bashni_sotovoy_svyazi