Способ ΣΔ-преобразования известен уже давно (с конца 50-х, начала 60-х годов прошлого века), однако прецизионные АЦП, основанные на этом способе, получили широкое распространение сравнительно недавно (с 90-х годов прошлого века) [1, 2, 3]. Это связано с тем, что практические реализации ΣΔ-АЦП в интегральном исполнении появились лишь, когда стали широко доступны сигнальные процессоры на цифровых КМОП-структурах, необходимые для реализации цифровых фильтров, являющихся неотъемлемой частью данного вида АЦП [2, 3]. В настоящее время освоена цифровая технология высокой плотности VLSI, позволяющая изготавливать и аналоговую и цифровую части на одном кристалле и, тем самым, заметно снизить стоимость производства интегральных микросхем (ИМС) [4].
Высокая разрядность современных ΣΔ-АЦП достигается за счет использования большого числа различных способов и технологий, совершенствующих базовую структуру преобразователя, состоящую из ΣΔ-модулятора 1-го порядка и простого усредняющего цифрового фильтра [1, 2], при этом сложность АЦП возрастает на несколько порядков. С другой стороны, применение данных технологий в ряде случаев ухудшает эксплуатационные характеристики преобразователей, и ограничивает возможности их использования в некоторых областях техники. Например, один из основных способов совершенствования ΣΔ-АЦП заключается в повышении порядка модулятора, другими словами в увеличении числа интегрирующих и суммирующих звеньев [1, 2]. Однако при использовании модуляторов 3-го и более высоких порядков появляется возможность возникновения неустойчивого состояния АЦП [1], что противоречит требованиям надежности и эффективности, предъявляемым к АЦП в таких областях, как системы телеметрического контроля ракетно-космической техники, техника медицины катастроф и др.
Анализ работы ΣΔ-АЦП во временной области, проведенный в [5], показал возможность повышения точности преобразования базовой структуры с помощью адаптивной обработки выходных данных. Достоинством данного подхода является тот факт, что использование адаптивной обработки не отменяет большинства известных [1] способов повышения точности преобразования, и может применяться совместно с ними. В данной статье предлагается алгоритм адаптивной обработки данных для ΣΔ-АЦП, основанный на методе кодирования Лемпеля-Зива-Велча.
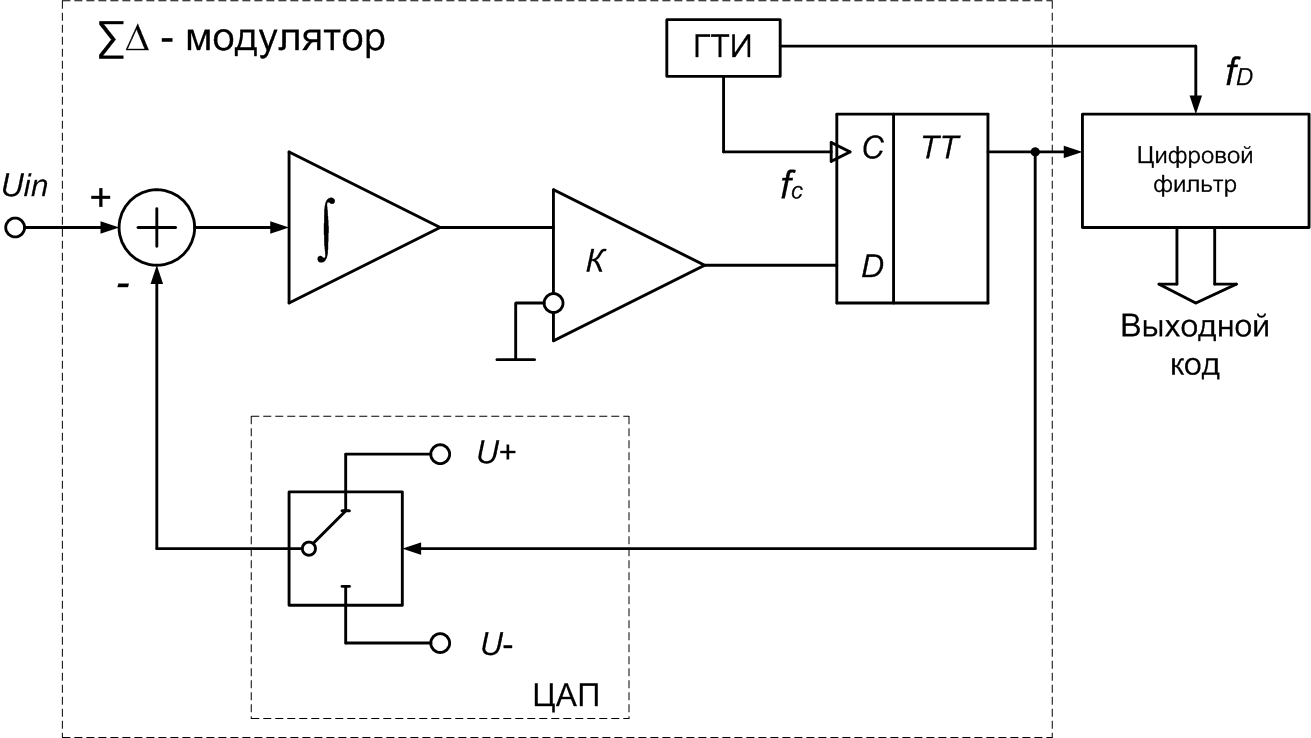
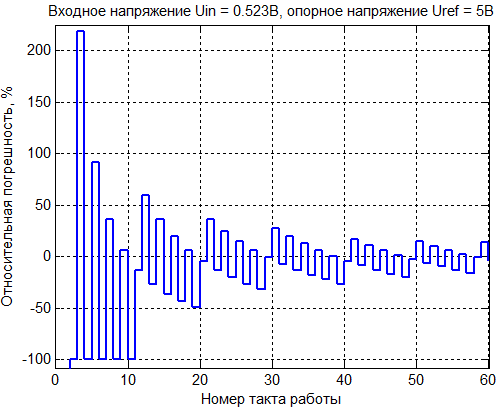
Аналогично работе [5] в качестве объекта исследования была выбрана базовая структура ΣΔ-АЦП, представленная на рисунке 1. ΣΔ-модулятор осуществляет развертывание входного напряжения в координату развертывания – время, формируя в процессе работы выходной бинарный код, который представляет собой последовательность 0 и 1, синхронизированных с частотой fc тактового генератора и определяющих подключение отрицательной и положительной опор 1-разрядного ЦАП соответственно. Характер структуры данного сигнала определяется входным напряжением. Примеры выходных кодов ΣΔ-модулятора для двух значений входного напряжения показаны на рисунке 2.
Р исунок
1 - ΣΔ-АЦП с модулятором 1-го порядка (ʃ
- интегратор, K
– компаратор, ГТИ – генератор тактовых импульсов, TT
– D-триггер,
fc
– частота работы модулятора, fD
частота дискретизации входного сигнала Uin)
исунок
1 - ΣΔ-АЦП с модулятором 1-го порядка (ʃ
- интегратор, K
– компаратор, ГТИ – генератор тактовых импульсов, TT
– D-триггер,
fc
– частота работы модулятора, fD
частота дискретизации входного сигнала Uin)
Рисунок 2 - Выходные бинарные последовательности ΣΔ-модулятора 1-го порядка
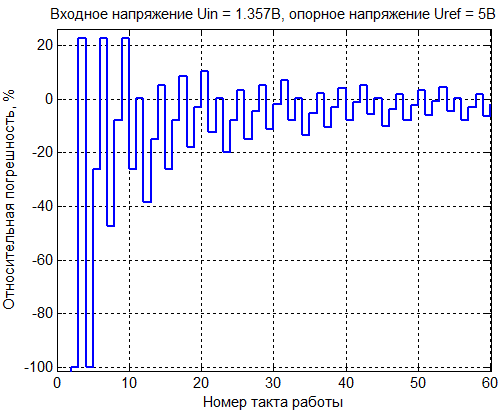
Результат преобразования определяется усреднением заданной выборки выходной последовательности. Согласно теории [6] точность получаемого результата преобразования зависит от длительности интервала преобразования, другими словами объема усредняемой выборки. На рисунке 3 приведены графики зависимости относительной погрешности преобразования от количества тактов работы вошедших в интервал преобразования. Как видно из рисунка 3 для конкретного значения входного сигнала при различных интервалах преобразования результат может быть вычислен как с большей, так и с меньшей погрешностью. Очевидно, что для одного и того же интервала преобразования погрешность преобразования различных входных значений будет различна. Например, задав результат преобразования равным 50 тактам, для значения входного напряжения 1.357В имеем относительную погрешность 3.1688 %, а для входного напряжения 0.523В – 14,7228 %.
Рисунок 3 - Графики распределения погрешности расчета входной величины по выходным данным от объема усредняемой выборки
В классической обработке при вычислении результата преобразования усредняются все значения выходного кода вошедшие в интервал преобразования (подробное см. [1]). Задача адаптивной обработки заключается в определении необходимого объема усредняемой выборки, на интервале преобразования. Причем длительность интервала преобразования остается неизменной и определяется частотой дискретизации входного сигнала.
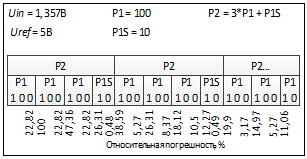
В работе [5] показано, что структура выходного кода модулятора связана со структурой погрешности преобразования. Данную связь поясняет рисунок 4. Таким образом, определяя структуру выходного кода можно решить задачу определения необходимого объема усредняемых данных на интервале преобразования, для получения более точного результата.
Рисунок 4 – Структура последовательности при входном напряжении 1,357В
При разработке соответствующего алгоритма за основу был взят метод сжатия данных без потерь Лемпеля-Зива-Велча, идея которого состоит в том, что вместо последовательностей букв передаются номера слова в некотором словаре. Кодер и декодер в процессе работы синхронно формируют словарь. На каждом шаге словарь пополняется одним новым словом, которое до этого в словаре отсутствовало, но является продолжением на одну букву одного из слов словаря [7]. Метод Лемпеля-Зива-Велча при кодировании динамически создает таблицу преобразования строк. По мере кодирования, просматривает текст символ за символом, и сохраняет каждую новую, уникальную бинарную строку в таблицу в виде пары код/символ. Таким образом, данный метод при решении задачи строит алфавит последовательности символов, именно поэтому метод Лемпеля-Зива-Велча был взят нами за основу, потому что выявляемые структуры фактически можно рассматривать как буквы, а их совокупность - как алфавит.
Однако прямое применение данного метода не подходит для решения поставленной задачи, так как на выходе получается множество лишних букв, ведь в методе Лемпеля-Зива-Велча каждая буква состоит из какой-нибудь существующей буквы в алфавите плюс еще один символ. Поэтому решено разработать собственный алгоритм построения алфавита, поиска самой старшей буквы и вычисления результата преобразования.
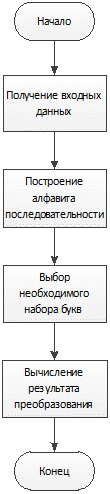
Принцип работы разработанного алгоритма заключается в поиске повторяющихся частей последовательности и замены их на новые буквы алфавита. Сначала происходит анализ выходной последовательности в виде бинарного кода и ее преобразование в буквенную форму. Затем происходит компоновка всех получившихся букв в один массив. Среди них определяется самая старшая буква или совокупность целого числа старших букв в анализируемом массиве, соответствующем интервалу преобразования. По выборке данной буквы производиться вычисление результата преобразования. Разработанный алгоритм представлен в виде блок-схемы на рисунке 5. Процедура построения алфавита последовательности подробно описана в [8].
Рисунок 5 - Блок-схема разработанного алгоритма
Разработанный алгоритм был реализован в пакете математического моделирования MATLAB 2010b в виде программы. С целью проверки эффективности разработанного алгоритма проведен сравнительный анализ результатов преобразования классическим способом и с помощью адаптивной обработки. В анализе использовалась Simulink-модель ΣΔ-модулятора 1-го порядка в качестве входного сигнала, которой задавались значения, имитирующие постоянное напряжение. Результаты сравнительного анализа представлены в таблице 1.
Таблица 1
Результаты сравнительного анализа классического способа преобразования и предложенного алгоритма
|
Входное напряжение, В |
Результат преобразования (классический способ), В |
Относительная погрешность преобразования, % |
Результат преобразования (предложенный алгоритм), В |
Относительная погрешность преобразования, % |
|
Интервал преобразования 128 тактов | ||||
|
0,376 |
0,3906 |
3,8830 |
0,3763 |
0,0798 |
|
1,370 |
1,3281 |
3,0584 |
1,3636 |
0,4672 |
|
2,741 |
2,7344 |
0,2408 |
2,7419 |
0,0328 |
|
3,348 |
3,3594 |
0,3405 |
3,3486 |
0,0179 |
|
4,235 |
4,2188 |
0,3825 |
4,2373 |
0,0543 |
|
Интервал преобразования 256 тактов | ||||
|
0,376 |
0,3906 |
3,8830 |
0,3763 |
0,0798 |
|
1,370 |
1,3672 |
0,2044 |
1,3704 |
0,0292 |
|
2,741 |
2,7344 |
0,2408 |
2,7419 |
0,0328 |
|
3,348 |
3,3203 |
0,8274 |
3,3482 |
0,0060 |
|
4,235 |
4,2188 |
0,3825 |
4,2405 |
0,1299 |
Из таблицы можно сделать вывод, что предложенный алгоритм производит преобразования с меньшей погрешностью в сравнении с классическим способом. Таким образом, алгоритм адаптивной обработки на основе метода кодирования Лемпеля-Зива-Велча, позволяет повысить точность преобразования базовой структуры ΣΔ-АЦП и является альтернативой алгоритму адаптивной обработки, основанному на нахождении нулей первой разности вычисленных значений, описанному в [5]. Предложенный алгоритм может быть использован при синтезе систем цифровой обработки прецизионных ΣΔ-АЦП.
Литература:
1. У. Кестер. Аналого-цифровое преобразование/ перевод с английского под редакцией Володина Е.Б. // М.: Техносфера, 2007 – 1016с
2. Э.К. Шахов. ΣΔ-АЦП: Процессы передискретизации, шейпинга шума квантования и децимации // Датчики и системы. № 11, 2006 г., с 50 – 57.
3. В.Н. Ашанин, Б.В. Чувыкин, Э.К. Шахов. ΣΔ-аналого-цифровые преобразователи: основы теории и проектирования. – Пенза: Информационно-издательский центр ПензГУ, 2009 г. – 188с.
4. Г. И. Волович. Схемотехника аналоговых и аналого-цифровых электронных устройств. - М.: Издательский дом «Додэка-ХХI», 2005. - 528 с.
5. В.А. Юрманов, К.Ю. Пискаев, А.В. Куц. ΣΔ-АЦП: адаптивная обработка результатов преобразования. // Вопросы радиоэлектроники. Серия ОТ. Выпуск 2. Изд-во: ОАО «ЦНИ «Электроника», Москва, 2011 г. С. 92 – 101.
6. Э.К. Шахов, В.Д. Михотин. Интегрирующие развертывающие преобразователи напряжения. – М.: Энергоатомиздат, 1986 г. - 144 с.
7. Б.Д. Кудряшов. Теория информации: учебник для вузов. – СПб.: Питер, 2009г.
8. К.Ю. Пискаев, В.С. Подшивалов, М.В. Кяшкин. Алгоритм автоматического анализа выходных данных ΣΔ-АЦП на основе метода кодирования Лемпеля-Зива-Велча // Труды международной научно-технической конференции «Современные информационные технологии». – Пенза: Пензенская Государственная Технологическая Академия, 2011 год, выпуск 13, с.51-57.