Принципы проектирования систем автоматизации повышенной отказоустойчивости и надежности

В условиях непрерывного совершенствования и усложнения технологических процессов крайне важной задачей становится разработка методов повышения достоверности преобразования измерительной информации, алгоритмов многоступенчатой аналоговой, цифровой и логической фильтрации сигналов, а также базы правил, определяющих поведение системы автоматизации в условиях неопределенности. Статья посвящена описанию алгоритмов, позволяющих увеличить надежность центрального узла всех систем автоматизации – микропроцессорного контроллера.

В современных технологических процессах большую роль играют информационно-измерительные системы. Сравнительно недавно в промышленности стали применяться гибкие автоматизированные информационные системы сбора, интерпретации и первичного анализа данных, центральным узлом которых является способный реализовывать сложнейшие алгоритмы обработки сигналов микропроцессор. В реальных условиях на такие системы воздействует окружающая среда, что проявляется в наличии многочисленных механических и электрических помех. Кроме того, существуют ситуации, в которых контроллер системы сбора информации должен реагировать на какие-либо события в течение кратчайшего промежутка времени (долей микросекунд и др.).

Во многих случаях сигналом измерительной информации является время регистрации какого-либо импульсного сигнала. К примеру, принцип действия ультразвуковых уровнемеров основан на определении уровня жидкости по времени распространения импульсов ультразвуковой частоты. В момент времени T₀ ультразвуковой передатчик излучает сигнал — пачку импульсов продолжительностью , которая распространяется в окружающей среде со скоростью звука. Когда сигнал достигает объекта, то его часть отражается и приходит в приёмник в момент времени T1. Электронная схема устройства обработки сигнала определяет расстояние до объекта, измеряя время T₁ – T₀. Недостатком этого метода является относительно большое минимальное расстояние обнаружения: отражённые сигналы от объектов, расположенных очень близко к датчику, поступают раньше окончания спада импульса из­лучателя и по этой причине не могут быть обработаны. Любая помеха может быть воспринята в качестве сигнала измерительной информации и, таким образом, датчик будет определять несуществующее значение.

Другой пример – поплавковый магнитострикционный датчик уровня. Принцип действия этих уровнемеров основан на эффекте магнитострикции. Микроконтроллер выдает импульс тока в катушку чувствительного элемента датчика, выполненного в виде длинной стальной проволоки. Под действием магнитного поля магнита, надетого на проволоку - звукопровод поплавка, и импульса тока катушки, намотанной на звукопровод, возникает импульс деформации, который, распространяясь по звукопроводу вверх, достигает пьезоэлектрического преобразователя. В датчиках измеряется время от формирования импульсов тока до момента приема импульсов упругой деформации, принятых и преобразованных пьезоэлектрическим преобразователем. Это позволяет определить расстояние до местоположения поплавка, определяемого положением уровня жидкости.[1]

Таким образом, вышеуказанные датчики фиксируют время пребывания импульсного сигнала, распространяющегося со скоростью звука. Ширина таких импульсов составляет несколько микросекунд. Следовательно, для их уверенного распознавания контроллер датчика должен производить вычисления, включающие в себя математические преобразования и проверку функционально-логических критериев, в течение долей микросекунд. Современным процессорам это не составляет трудности, но в условиях производственного шума, вибрации, электрических и магнитных помех данная задача может привести к некорректной работе программного обеспечения датчика, искажению результатов и др.

Далее приводятся успешно применяемые на практике алгоритмы проектирования «интеллектуальных» микропроцессорных систем автоматизации, разработанные с целью увеличения надежности, помехозащищенности преобразователей информации и повышения точности извлечения данных из временных интервалов распространения импульсных сигналов.

1. Защита от импульсных помех на аппаратном уровне

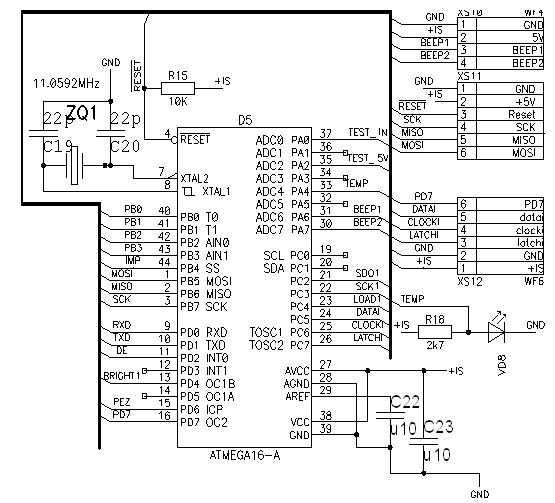
Одним из самых высокопроизводительных и надежных микропроцессоров является микроконтроллер AVR (рис.1). В нем предусмотрено наличие специального вывода ICP (Input capture pin, порт PD6) – вывода захвата на входе. Опрос такого входа производится при каждом инкременте содержимого аппаратного таймера-счетчика. К примеру, если в системе используется кварцевый резонатор, задающий частоту 11,0592 МГц, а коэффициент деления таймера выбран равным 8, то частота таймера составляет 11,0592 МГц/8=1,3824 МГц, и период опроса данных на дискретном входе равен 1/1382400 мкс=0,7 мкс. При ширине импульсов, равной (7-10) мкс, на один импульс приходится 10-15 отсчетов таймера, что вполне удовлетворяет требованиям четкого распознавания переднего и заднего фронтов каждого импульса. [2]

Основное преимущество от использования ICP – наличие встроенной автоматической логической фильтрации данных, поступающих на этот вывод. Импульсы длительностью менее 4 тактов таймера (3 мкс) игнорируются. То есть, запись времени в тактах поступления переднего фронта импульса на вывод ICP произойдет только в том случае, если будут распознаны четыре последовательных высоких уровня сигнала на этом выводе. Таким образом, импульсные помехи длительностью менее 3 мкс подавляются на аппаратном уровне, что позволяет не учитывать их при разработке алгоритмов обработки данных. Кроме того, при изменении уровня сигнала на выводе ICP генерируется аппаратное прерывание, что существенно упрощает процесс написания исходного кода программного обеспечения и делает его более структурированным.[2]

Рис.1. Микроконтроллер AVR Atmega16-16AU.

2. Применение адаптивных алгоритмов предсказания сигнала на шаг вперед

Во многих случаях полезно сравнить полученное значение сигнала измерительной информации с заранее спрогнозированным с целью исключения выбросов и неопределенностей в показаниях датчика. Большинство известных приемов прогнозирования значения целевого сигнала используют методы экстраполяции. Но следует выделить ситуации, при которых измерительную информацию несут в себе такие физические параметры, как время распространения звуковой волны, скорость электромагнитных волн в среде и др. В этих случаях между двумя измерениями проходит интервал в несколько микросекунд, что крайне недостаточно для надлежащей обработки сигналов даже самыми быстрыми процессорами. Кроме того, различные механические воздействия на измерительную систему, проявляющиеся в виде кратковременных импульсных помех, делают невозможными применение для реализации функции предсказания методов экстраполяции.

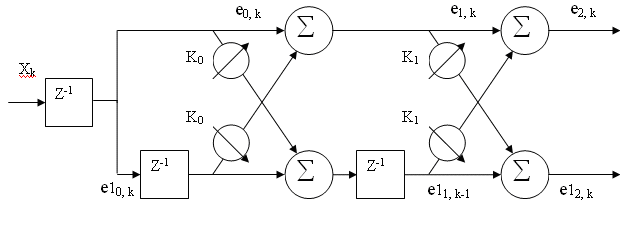
Одним из самых эффективных алгоритмов прогнозирования текущего значения сигнала по двум предыдущим является применение адаптивных решеток. На рисунке 2 представлена схема этой структуры, причем весовые коэффициенты (K₀ и K₁) являются переменными во времени. [4, с. 262-268]

Для рассматриваемой схемы рекуррентные соотношения имеют вид:

E[0,k]=X[k-1] (1)

E1[0,k]=X[k-1]

E[1,k]=E[0,k]+K₀*E1[0,k-1]

E[2,k]=E[1,k]+K₁*E1[1,k-1]

E1[1,k]=K₀*E[0,k]+E1[0,k-1]

E1[2,k]= K₁*E[1,k]+E1[1,k-1]

После одной итерации вычислений следует внести поправку в величину коэффициентов K₀ и K₁:

K₀= K₀-2*m0*E[1,k]*E1[0,k-1] (2)

K₁= K₁-2*m1*E[2,k]*E1[1,k-1]

Коэффициенты m0 и m1 не являются функциями времени, но их рекомендуется задать равными (0.8-0.9) и постепенно уменьшать до значения (0.1-0.2).

Рис.2. Структура адаптивной решетки прогнозирования сигнала.

Для прогнозирования очередного значения сигнала X_k, мерой которого является Y_k, используется формула [2]:

Y[k]=-K₀*(K₁+1)*X[k-1]- K₁* X[k-2]+E[2,k]

3. Цифровая обработка сигналов с целью устранения высокочастотных шумов

Все алгоритмы цифровой обработки сигналов, как правило, – блочного типа, построены на сколь угодно сложных комбинациях достаточно небольшого набора типовых цифровых операций, к которым относятся рекуррентные вычисления, фильтрация и функциональные преобразования. Задача цифровой фильтрации в большинстве случаев имеет цель выделение цифровым вычислительным устройством (ЦВУ, микропроцессором) полезного сигнала (как правило, низкочастотного), или, что равноценно, удаление высокочастотного шума из входного сигнала. [5]

Основными достоинствами цифровых фильтров являются:

1. наличие параметров, реализация которых невозможна в аналоговых фильтрах, например, линейной фазовой характеристики, простота программной реализации;

2. отсутствие необходимости периодического контроля и калибровки, т.к. работоспособность фильтров не зависит от дестабилизирующих факторов внешней среды;

3. один фильтр может обрабатывать несколько входных каналов;

4. входные и выходные данные можно сохранять для последующего использования;

5. точность цифровых фильтров ограничена только используемой разрядностью отсчетов (длиной слов);

6. фильтры могут использоваться на очень низких частотах и в большом диапазоне частот, для чего достаточно только изменять частоту дискретизации данных;

Самым распространенным алгоритмом выделения полезного сигнала на фоне высокочастотных помех является метод наименьших квадратов (МНК). Простейший способ аппроксимации по МНК произвольной функции s(t) - с помощью полинома первой или второй степени, т.е. функции вида y(t) = A+Bt+Сt². Для определения коэффициентов полинома необходимо найти минимум функции приближения (функцию остаточных ошибок). С учетом дискретности данных по точкам t_n = n&#;t, функция остаточных ошибок записывается в форме:

&#;(A,B,C) = [s_n-(A+B·n+C·n²)]².

Система уравнений после дифференцирования выражения (3.2.1) по А, В, С и приравнивания полученных выражений нулю:

A1 + Bn + Сn² =s_n.

An + Bn² + Сn³ =n·s_n.

An² + Bn³ + Сn⁴ =n²·s_n.

Решая систему уравнений относительно А, получаем:

A = {n⁴s_n -n²n²s_n} / {1n⁴ - [n²]²}.

При распространении последнего выражения для 5-ти точечного МНК:

y_o = (17s_n - 5n²s_n) /35 = (-3·s_-2+12·s_-1+17·s_o+12·s₁-3·s₂) /35, или в рекуррентной форме Y[k]=1/35(-3X_k-2+12X_k-1+17X_k+12X_k+1+3X_k+2).

Подставляя значение s_n = и объединяя комплексно сопряженные члены, получаем частотную характеристику 5-ти точечного сглаживающего фильтра МНК второго порядка [5]:

H(&#;) =1/35(17+24 cos(&#;&#;-6 cos(2&#;))

Указанную частотную характеристику можно оптимизировать, полагая, что на границе допустимого интервала дискретизации ее значение равно 0, то есть H()=0:

H() =1/а(17+24 cos(&#;+bcos(2))=0, где

а – сумма модулей коэффициентов частотной характеристики фильтра;

b – неизвестный параметр.

После вычислений получаем:

17-24+2b=0; b=3.5; а=17+24+3.5=44.5

В результате окончательных преобразований (приведением параметра b к целому числу, умножая его на 4) получаем скорректированную частотную характеристику фильтра:

H(&#;) =1/178(68+96cos(&#;&#;+14cos(2&#;))

Рис.3. Частотная характеристика фильтров МНК второго порядка.

Как видно из рисунка 3, полоса частот пропускания такого фильтра лежит в диапазоне (0.2-0.3) частоты дискретизации, что позволяет с большой точностью устранить шумовую составляющую, частота которой в десятки раз превышает частоту дискретизации.

4. Цифровая обработка сигналов с целью устранения низкочастотных шумов

В современных компьютерных сетях и системах дистанционной передачи и обработки информации большое значение имеет достоверность передачи сигнала. В большинстве случаев частотный спектр помехи намного отличен от частотного спектра полезного сигнала. При этом достаточно применить обычный цифровой фильтр низких частот. Но существуют системы, в которых частотные спектры полезного сигнала и помехи перекрываются, то есть являются сопоставимыми – низкочастотными. Например, линия связи искажает передаваемые сигналы из-за того, что ее физические параметры отличаются от идеальных: медные провода всегда представляют собой некоторую распределенную по длине комбинацию активного сопротивления, емкостной и индуктивной нагрузок.

Целью устранения низкочастотных помех является определение частотных характеристик линейного фильтра, входной сигнал которого – зашумленный сигнал f(t)=x_пол(t)+x_случ(t), а выходной – процесс β(t) с известными (заданными аналитически) вероятностными характеристиками (спектральной плотностью) по соотношению , где - желаемая спектральная плотность сигнала на выходе фильтра, -спектральная плотность случайного процесса f(t), -АЧХ фильтра.[3]

Таким образом, комплексное использование всех рассмотренных методов позволяет резко сократить вероятность отказов автоматизированных информационно-измерительных систем, одновременно увеличив надежность и достоверность происходящих в них вычислительных процессов. Все рассмотренные в статье принципы успешно применены при разработке запатентованного датчика - магнитострикционного двухимпульсного уровнемера [1].

Литература:

1. Патент РФ на полезную модель № 93976. Поплавковый уровнемер / Илясов Л.В., Требухин А.Г.

2. Свидетельство о государственной регистрации программы для ЭВМ № 2010610284 «Интеллектуальный микропроцессорный интерпретатор сигналов магнитострикционного преобразователя уровня» / Требухин А.Г.

3. Свидетельство о государственной регистрации программы для ЭВМ № 2009613764 «Параметрическая идентификация линейного фильтра для подавления помех с частотным спектром, сравнимым с частотным спектром полезного сигнала» / Требухин А.Г. , Васильев В.Г.

4. Уидроу Б., Стирнз С. Адаптивная обработка сигналов: Пер. с англ. – М.: Радио и связь, 1989. – 440с.

5. http://prodav.narod.ru/student/