В статье авторы описывают анализ классификаторов тональности текста, которые можно использовать для определения фейковых новостей.
Ключевые слова: фейковые новости, анализ тональности, классификация.
Введение
В наше время одним из важных аспектов повседневной жизни является информационная сфера. Информации, которую можно получить, а также способов её получения с каждым днём всё больше, что, разумеется, влияет и на её качество. Информационная среда является очень динамичной и быстро развивающейся, что влечет за собой необходимость её урегулирования. Проблема правового регулирования должна подниматься на федеральном уровне.
В настоящее время на территории РФ действует Федеральный закон от 27 июля 2006 года № 149-ФЗ «Об информации, информационных технологиях и о защите информации», который заменил собой Федеральный закон от 20 февраля 1995 года № 24-ФЗ «Об информации, информатизации и защите информации» [1] и Федеральный закон от 4 июля 1996 года № 85-ФЗ «Об участии в международном информационном обмене». [2]
18 марта 2019 года в закон «Об информации…» была внесена статья 151’1, определяющая порядок ограничения доступа к информации, «выражающей в неприличной форме, которая оскорбляет человеческое достоинство и общественную нравственность, явное неуважение к обществу, государству, официальным государственным символам Российской Федерации, Конституции Российской Федерации или органам, осуществляющим государственную власть в Российской Федерации» [3].
Действительно, данная статья была своевременно внесена в качестве поправки в Федеральный закон. В последнее время в интернете появилось огромное количество провокационных и оскорбительных материалов, которые оскорбляют наше Государство, нашу историю и выражают явное неуважение и даже пренебрежение нашим обществом.
1. Понятие «фейковых новостей»
Понятие «фейк» (от англ. fake — «подделка» или «фальшивка») включает в себя различные явления (в данном контексте) медиасреды: поддельные тексты, сфабрикованные аудио-, видео- и фотоматериалы. Кроме того, это понятие включает в себя не только саму поддельную информацию, но и способы её распространения. Например, к это категории относятся искусственно созданные проекты, издания, публичные личности, фальшивые аккаунты, нативная реклама. [4] Сама же «фейковая новость» определяется как «сообщение, стилистически созданное как настоящая новость, но ложное полностью или частично».
2. Основные понятия классификации
Одной из задач информационного поиска является классификация документов. Её суть заключается в том, что необходимо на основании содержания документа отнести его к одной из нескольких категорий.
В случае формализации задачи можно определить ей так:
Пусть существует множество документов
(1),
множество категорий
(2)
И неизвестная целевая функция
(3)
Необходимо построить такой классификатор 
, который будет максимально близким к 
Для осуществления классификации берется начальная коллекция размеченных документов:
(4),
Разделенная на две части. Первая, она же «обучающая» необходима для обучения классификатора, вторая же является «проверочной» и осуществляет независимую проверку качества проведенного обучения.
В конечном итоге классификатор может выдать либо точный ответ:
(5)
Либо степень подобия:
(6)
Итак, задача классификации текстов поставлена. Теперь определим, что такое анализ тональности текста.
Анализ тональности (Sentiment analysis) — это область компьютерной лингвистики, которая занимается изучением мнений и эмоций в текстовых документах [5].
Основной целью анализа тональности текста является нахождение мнений в нем определение их главных свойств. В зависимости от типа анализа, нам могут понадобиться различные свойства. Например, это может быть автор мнения, тема текста, с которым мы работаем или настроение автора, относительно данной темы.
3. Методики оценки
Для сравнения алгоритмов между собой необходимо ввести функцию, описывающую качество классификации. Определим матрицу ошибок.
Для задачи классификации на два класса нам понадобится матрица 
. В таблице 1 описана матрица ошибок для задачи классификации.
Таблица 1
Матрица ошибок для задачи классификации
|
|
|
|
|
|
True Positive, истинно положительные (TP) — количество объектов, относящихся к классу 1 и классифицированных как 1 |
False Positive, ложноположительные (FP) — количество объектов, относящихся к классу 0 и классифицированных как 1 (ошибка) |
|
|
False Negative, ложноотрицательные (FN) — количество объектов, относящихся к классу 1 и классифицированных как 0 (ошибка) |
True Negative, истинно отрицательные (TN) — количество объектов, относящихся к классу 0 и классифицированных как 0 |
Далее введем понятие доли правильных ответов (accuracy). Оно будет описываться как отношение количества правильно классифицированных объектов к общему количеству объектов:
(7)
Чтобы оценить качество работы алгоритма, введем метрики точности (precision) и полноты (recall), которые будут определяться формулами:
(8)
(9),
Где точность — это доля объектов, названных классификатором положительными и являющихся положительными, а полнота — доля положительных объектов из всех положительных объектов.
Для оценки мы объединим их в общую F-меру качества:
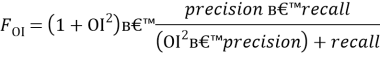(10) –
Среднее гармоническое, где 
определяет вес точности в метрике.
4. Алгоритмы для сравнения качества классификации
Для сравнения алгоритмов задача классификации была разбита на:
- Векторизацию текста
- Трансформацию векторов
- Классификацию
Для каждого шага выбиралось несколько моделей, решающих эти задачи, и проводилось их сравнение. Шаги комбинировались для всех возможных вариантов и измерялась точность классификации.
Для шага векторизации сравнивались:
- Униграммы
- Униграммы и биграммы
- Биграммы
Для шага векторизации:
1. Линейный TF
2. Логарифмический TF
3. Линейный TF-IDF
4. Логарифмический TF-IDF
Для классификации:
1. Метод K ближайших соседей
2. Метод опорных векторов с линейным ядром
3. Метод опорных векторов с ядром RBF (радиальная базисная функция)
4. Дерево решений
5. Метод «случайного леса»
6. AdaBoost
7. Многомерный наивный Байесовский классификатор
8. Сверточные нейронные сети
5. Результаты оценки
Для оценки доли правильных ответов была написана программа на языке python.
Обучение производилось на датасете с «положительными» и «отрицательными» русскоязычными твитами.
В результате была получена таблица 2. Кроме того, программа строит графики для наглядности сравнения.
На рисунках 1, 2, 3 представлены графики наилучшей F-меры классификации.
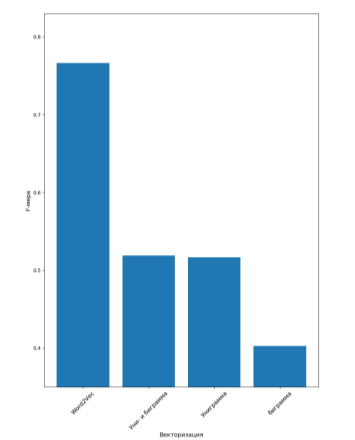
Рис. 1. Наилучшая F-мера для векторизации
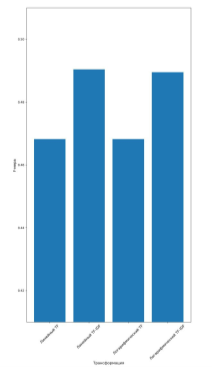
Рис. 2. Наилучшая F-мера для трансформации
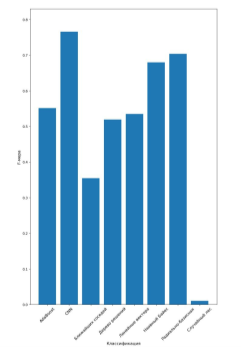
Рис. 3. Наилучшая F-мера для классификации
Проанализировав полученные результаты, можно сделать вывод о том, что нейронные сети превосходят остальные алгоритмы. Наилучшими по точности являются Байесовский и радиально-базисный классификаторы.
Таблица 2
Результаты сравнения доли правильных ответов
|
Векторизация |
Трансформация |
Классификация |
accuracy |
f1_score |
fscore_1 |
fscore_2 |
precision_1 |
precision_2 |
recall_1 |
recall_2 |
|
Униграмма |
Логарифмический TF |
Ближайших соседей |
0,524 |
0,150 |
0,669 |
0,150 |
0,509 |
0,779 |
0,976 |
0,083 |
|
Униграмма |
Логарифмический TF |
Линейные вектора |
0,675 |
0,677 |
0,672 |
0,677 |
0,668 |
0,680 |
0,675 |
0,674 |
|
Униграмма |
Логарифмический TF |
Радиально-базисная |
0,725 |
0,727 |
0,723 |
0,727 |
0,718 |
0,731 |
0,727 |
0,722 |
|
Униграмма |
Логарифмический TF |
Дерево решений |
0,615 |
0,619 |
0,611 |
0,619 |
0,609 |
0,620 |
0,612 |
0,617 |
|
Униграмма |
Логарифмический TF |
Случайный лес |
0,495 |
0,009 |
0,661 |
0,009 |
0,494 |
0,727 |
0,998 |
0,005 |
|
Униграмма |
Логарифмический TF |
AdaBoost |
0,651 |
0,640 |
0,661 |
0,640 |
0,634 |
0,670 |
0,691 |
0,612 |
|
Униграмма |
Логарифмический TF |
Наивный Байес |
0,708 |
0,696 |
0,718 |
0,696 |
0,685 |
0,735 |
0,755 |
0,661 |
|
Униграмма |
Линейный TF |
Ближайших соседей |
0,526 |
0,160 |
0,670 |
0,160 |
0,510 |
0,777 |
0,974 |
0,089 |
|
Униграмма |
Линейный TF |
Линейные вектора |
0,673 |
0,675 |
0,671 |
0,675 |
0,666 |
0,679 |
0,675 |
0,671 |
|
Униграмма |
Линейный TF |
Радиально-базисная |
0,722 |
0,724 |
0,719 |
0,724 |
0,716 |
0,727 |
0,723 |
0,721 |
|
Униграмма |
Линейный TF |
Дерево решений |
0,615 |
0,619 |
0,610 |
0,619 |
0,609 |
0,620 |
0,611 |
0,618 |
|
Униграмма |
Линейный TF |
Случайный лес |
0,494 |
0,006 |
0,661 |
0,006 |
0,494 |
0,667 |
0,998 |
0,003 |
|
Униграмма |
Линейный TF |
AdaBoost |
0,652 |
0,635 |
0,667 |
0,635 |
0,631 |
0,677 |
0,708 |
0,597 |
|
Униграмма |
Линейный TF |
Наивный Байес |
0,707 |
0,695 |
0,718 |
0,695 |
0,684 |
0,734 |
0,755 |
0,660 |
|
Униграмма |
Логарифмический TF-IDF |
Ближайших соседей |
0,555 |
0,369 |
0,656 |
0,369 |
0,530 |
0,653 |
0,860 |
0,257 |
|
Униграмма |
Логарифмический TF-IDF |
Линейные вектора |
0,660 |
0,663 |
0,657 |
0,663 |
0,654 |
0,666 |
0,660 |
0,660 |
|
Униграмма |
Логарифмический TF-IDF |
Радиально-базисная |
0,717 |
0,718 |
0,716 |
0,718 |
0,709 |
0,726 |
0,724 |
0,710 |
|
Униграмма |
Логарифмический TF-IDF |
Дерево решений |
0,615 |
0,618 |
0,613 |
0,618 |
0,609 |
0,622 |
0,617 |
0,614 |
|
Униграмма |
Логарифмический TF-IDF |
Случайный лес |
0,496 |
0,035 |
0,659 |
0,035 |
0,495 |
0,568 |
0,986 |
0,018 |
|
Униграмма |
Логарифмический TF-IDF |
AdaBoost |
0,650 |
0,632 |
0,666 |
0,632 |
0,629 |
0,675 |
0,707 |
0,594 |
|
Униграмма |
Логарифмический TF-IDF |
Наивный Байес |
0,711 |
0,699 |
0,721 |
0,699 |
0,687 |
0,739 |
0,759 |
0,664 |
|
Униграмма |
Линейный TF-IDF |
Ближайших соседей |
0,559 |
0,382 |
0,657 |
0,382 |
0,533 |
0,656 |
0,855 |
0,269 |
|
Униграмма |
Линейный TF-IDF |
Линейные вектора |
0,660 |
0,661 |
0,659 |
0,661 |
0,653 |
0,668 |
0,665 |
0,655 |
|
Униграмма |
Линейный TF-IDF |
Радиально-базисная |
0,716 |
0,718 |
0,714 |
0,718 |
0,709 |
0,723 |
0,720 |
0,712 |
|
Униграмма |
Линейный TF-IDF |
Дерево решений |
0,615 |
0,618 |
0,612 |
0,618 |
0,609 |
0,621 |
0,615 |
0,615 |
|
Униграмма |
Линейный TF-IDF |
Случайный лес |
0,493 |
0,002 |
0,660 |
0,002 |
0,493 |
0,385 |
0,998 |
0,001 |
|
Униграмма |
Линейный TF-IDF |
AdaBoost |
0,649 |
0,639 |
0,660 |
0,639 |
0,633 |
0,668 |
0,688 |
0,612 |
|
Униграмма |
Линейный TF-IDF |
Наивный Байес |
0,709 |
0,697 |
0,719 |
0,697 |
0,686 |
0,735 |
0,755 |
0,663 |
|
Уни- и биграмма |
Логарифмический TF |
Ближайших соседей |
0,530 |
0,183 |
0,670 |
0,183 |
0,512 |
0,762 |
0,967 |
0,104 |
|
Уни- и биграмма |
Логарифмический TF |
Линейные вектора |
0,669 |
0,640 |
0,694 |
0,640 |
0,638 |
0,713 |
0,760 |
0,580 |
|
Уни- и биграмма |
Логарифмический TF |
Радиально-базисная |
0,724 |
0,726 |
0,721 |
0,726 |
0,719 |
0,729 |
0,724 |
0,724 |
|
Уни- и биграмма |
Логарифмический TF |
Дерево решений |
0,615 |
0,609 |
0,621 |
0,609 |
0,604 |
0,627 |
0,639 |
0,592 |
|
Уни- и биграмма |
Логарифмический TF |
Случайный лес |
0,498 |
0,022 |
0,662 |
0,022 |
0,496 |
0,789 |
0,997 |
0,011 |
|
Уни- и биграмма |
Логарифмический TF |
AdaBoost |
0,658 |
0,649 |
0,667 |
0,649 |
0,643 |
0,676 |
0,693 |
0,625 |
|
Уни- и биграмма |
Логарифмический TF |
Наивный Байес |
0,718 |
0,715 |
0,722 |
0,715 |
0,704 |
0,734 |
0,741 |
0,697 |
|
Уни- и биграмма |
Линейный TF |
Ближайших соседей |
0,531 |
0,190 |
0,670 |
0,190 |
0,513 |
0,762 |
0,965 |
0,109 |
|
Уни- и биграмма |
Линейный TF |
Линейные вектора |
0,669 |
0,640 |
0,693 |
0,640 |
0,638 |
0,712 |
0,759 |
0,580 |
|
Уни- и биграмма |
Линейный TF |
Радиально-базисная |
0,722 |
0,725 |
0,719 |
0,725 |
0,718 |
0,727 |
0,721 |
0,724 |
|
Уни- и биграмма |
Линейный TF |
Дерево решений |
0,616 |
0,617 |
0,614 |
0,617 |
0,609 |
0,623 |
0,620 |
0,612 |
|
Уни- и биграмма |
Линейный TF |
Случайный лес |
0,493 |
0,006 |
0,660 |
0,006 |
0,493 |
0,421 |
0,996 |
0,003 |
|
Уни- и биграмма |
Линейный TF |
AdaBoost |
0,657 |
0,647 |
0,666 |
0,647 |
0,640 |
0,675 |
0,694 |
0,620 |
|
Уни- и биграмма |
Линейный TF |
Наивный Байес |
0,717 |
0,714 |
0,720 |
0,714 |
0,704 |
0,732 |
0,738 |
0,697 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
Ближайших соседей |
0,562 |
0,367 |
0,665 |
0,367 |
0,534 |
0,685 |
0,882 |
0,250 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
Линейные вектора |
0,659 |
0,655 |
0,663 |
0,655 |
0,647 |
0,672 |
0,679 |
0,639 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
Радиально-базисная |
0,722 |
0,725 |
0,720 |
0,725 |
0,717 |
0,727 |
0,722 |
0,722 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
Дерево решений |
0,612 |
0,604 |
0,620 |
0,604 |
0,600 |
0,626 |
0,642 |
0,584 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
Случайный лес |
0,495 |
0,007 |
0,661 |
0,007 |
0,494 |
0,739 |
0,999 |
0,003 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
AdaBoost |
0,656 |
0,643 |
0,668 |
0,643 |
0,637 |
0,677 |
0,701 |
0,612 |
|
Уни- и биграмма |
Логарифмический TF-IDF |
Наивный Байес |
0,715 |
0,715 |
0,716 |
0,715 |
0,705 |
0,726 |
0,727 |
0,704 |
|
Уни- и биграмма |
Линейный TF-IDF |
Ближайших соседей |
0,562 |
0,377 |
0,663 |
0,377 |
0,535 |
0,675 |
0,871 |
0,261 |
|
Уни- и биграмма |
Линейный TF-IDF |
Линейные вектора |
0,659 |
0,655 |
0,663 |
0,655 |
0,647 |
0,672 |
0,680 |
0,639 |
|
Уни- и биграмма |
Линейный TF-IDF |
Радиально-базисная |
0,721 |
0,724 |
0,718 |
0,724 |
0,716 |
0,726 |
0,721 |
0,721 |
|
Уни- и биграмма |
Линейный TF-IDF |
Дерево решений |
0,611 |
0,596 |
0,624 |
0,596 |
0,596 |
0,628 |
0,656 |
0,566 |
|
Уни- и биграмма |
Линейный TF-IDF |
Случайный лес |
0,496 |
0,022 |
0,661 |
0,022 |
0,495 |
0,659 |
0,994 |
0,011 |
|
Уни- и биграмма |
Линейный TF-IDF |
AdaBoost |
0,656 |
0,643 |
0,667 |
0,643 |
0,638 |
0,677 |
0,700 |
0,612 |
|
Уни- и биграмма |
Линейный TF-IDF |
Наивный Байес |
0,713 |
0,712 |
0,713 |
0,712 |
0,703 |
0,723 |
0,724 |
0,702 |
|
Биграмма |
Логарифмический TF |
Ближайших соседей |
0,586 |
0,531 |
0,629 |
0,531 |
0,564 |
0,622 |
0,711 |
0,463 |
|
Биграмма |
Логарифмический TF |
Линейные вектора |
0,529 |
0,218 |
0,662 |
0,218 |
0,512 |
0,681 |
0,937 |
0,130 |
|
Биграмма |
Логарифмический TF |
Радиально-базисная |
0,653 |
0,668 |
0,636 |
0,668 |
0,659 |
0,647 |
0,614 |
0,690 |
|
Биграмма |
Логарифмический TF |
Дерево решений |
0,532 |
0,347 |
0,635 |
0,347 |
0,516 |
0,592 |
0,827 |
0,245 |
|
Биграмма |
Логарифмический TF |
Случайный лес |
0,494 |
0,003 |
0,661 |
0,003 |
0,494 |
0,778 |
1,000 |
0,001 |
|
Биграмма |
Логарифмический TF |
AdaBoost |
0,551 |
0,378 |
0,648 |
0,378 |
0,528 |
0,632 |
0,839 |
0,270 |
|
Биграмма |
Логарифмический TF |
Наивный Байес |
0,648 |
0,628 |
0,667 |
0,628 |
0,626 |
0,677 |
0,713 |
0,585 |
|
Биграмма |
Линейный TF |
Ближайших соседей |
0,587 |
0,534 |
0,630 |
0,534 |
0,565 |
0,624 |
0,711 |
0,467 |
|
Биграмма |
Линейный TF |
Линейные вектора |
0,529 |
0,221 |
0,662 |
0,221 |
0,512 |
0,680 |
0,936 |
0,132 |
|
Биграмма |
Линейный TF |
Радиально-базисная |
0,653 |
0,669 |
0,636 |
0,669 |
0,660 |
0,648 |
0,614 |
0,692 |
|
Биграмма |
Линейный TF |
Дерево решений |
0,532 |
0,344 |
0,636 |
0,344 |
0,516 |
0,591 |
0,828 |
0,243 |
|
Биграмма |
Линейный TF |
Случайный лес |
0,494 |
0,006 |
0,661 |
0,006 |
0,494 |
0,682 |
0,999 |
0,003 |
|
Биграмма |
Линейный TF |
AdaBoost |
0,551 |
0,367 |
0,652 |
0,367 |
0,528 |
0,640 |
0,852 |
0,257 |
|
Биграмма |
Линейный TF |
Наивный Байес |
0,647 |
0,627 |
0,666 |
0,627 |
0,625 |
0,675 |
0,711 |
0,585 |
|
Биграмма |
Логарифмический TF-IDF |
Ближайших соседей |
0,578 |
0,507 |
0,631 |
0,507 |
0,555 |
0,621 |
0,732 |
0,429 |
|
Биграмма |
Логарифмический TF-IDF |
Линейные вектора |
0,545 |
0,360 |
0,647 |
0,360 |
0,524 |
0,627 |
0,846 |
0,253 |
|
Биграмма |
Логарифмический TF-IDF |
Радиально-базисная |
0,646 |
0,663 |
0,626 |
0,663 |
0,653 |
0,639 |
0,602 |
0,688 |
|
Биграмма |
Логарифмический TF-IDF |
Дерево решений |
0,532 |
0,321 |
0,643 |
0,321 |
0,516 |
0,605 |
0,853 |
0,219 |
|
Биграмма |
Логарифмический TF-IDF |
Случайный лес |
0,494 |
0,006 |
0,661 |
0,006 |
0,494 |
0,700 |
0,999 |
0,003 |
|
Биграмма |
Логарифмический TF-IDF |
AdaBoost |
0,549 |
0,369 |
0,649 |
0,369 |
0,527 |
0,632 |
0,844 |
0,261 |
|
Биграмма |
Логарифмический TF-IDF |
Наивный Байес |
0,648 |
0,629 |
0,665 |
0,629 |
0,627 |
0,674 |
0,708 |
0,590 |
|
Биграмма |
Линейный TF-IDF |
Ближайших соседей |
0,579 |
0,509 |
0,632 |
0,509 |
0,556 |
0,622 |
0,732 |
0,430 |
|
Биграмма |
Линейный TF-IDF |
Линейные вектора |
0,546 |
0,359 |
0,648 |
0,359 |
0,524 |
0,628 |
0,847 |
0,252 |
|
Биграмма |
Линейный TF-IDF |
Радиально-базисная |
0,646 |
0,664 |
0,626 |
0,664 |
0,654 |
0,639 |
0,600 |
0,691 |
|
Биграмма |
Линейный TF-IDF |
Дерево решений |
0,532 |
0,322 |
0,643 |
0,322 |
0,516 |
0,605 |
0,853 |
0,220 |
|
Биграмма |
Линейный TF-IDF |
Случайный лес |
0,495 |
0,008 |
0,661 |
0,008 |
0,494 |
0,833 |
0,999 |
0,004 |
|
Биграмма |
Линейный TF-IDF |
AdaBoost |
0,550 |
0,377 |
0,647 |
0,377 |
0,528 |
0,630 |
0,837 |
0,269 |
|
Биграмма |
Линейный TF-IDF |
Наивный Байес |
0,649 |
0,630 |
0,666 |
0,630 |
0,627 |
0,675 |
0,709 |
0,590 |
|
Word2Vec |
CNN |
0,772 |
0,766 |
0,775 |
0,766 |
0,763 |
0,779 |
0,788 |
0,753 |
|
Литература:
- «Конституция Российской Федерации» (принята всенародным голосованием 12.12.1993) (с учетом поправок, внесенных Законами РФ о поправках к Конституции РФ от 30.12.2008 N 6-ФКЗ, от 30.12.2008 N 7-ФКЗ, от 05.02.2014 N 2-ФКЗ, от 21.07.2014 N 11-ФКЗ) // Справочно-правовая система Консультант Плюс.
- Федеральный закон от 27.07.2006 N 149-ФЗ (ред. от 03.04.2020) «Об информации, информационных технологиях и о защите информации» // Справочно-правовая система Консультант Плюс
- Федеральный закон от 4 июля 1996 года № 85-ФЗ «Об участии в международном информационном обмене» // Справочно-правовая система Консультант Плюс
- Клишин И. Максимальный ретвит: Фейк-пропаганда на новом уровне / И. Клишин // Ведомости. — 2014. — 12 февр.
- Обучаем компьютер чувствам (sentiment analysis по-русски), URL: https://habr.com/ru/post/149605/, // Электронный ресурс
