Как известно, проблема интерференции, т. е. взаимодействия скважин, является одной из важных задач в газовой промышленности. При интерференции скважин под влиянием изменения режима работы одной скважины изменяются дебиты, забойные давления других скважин, эксплуатирующих тот же пласт. При этом суммарная добыча газа из месторождений с вводом в эксплуатацию новых скважин растет медленнее, чем число скважин.
В данной статье рассматривается интерференция произвольного числа скважин с удаленным контуром питания с учетом влияния начального градиента давления.
Ключевые слова: интерференция, взаимодействия скважин, дебит, пласт, начальный градиент давления, газ.
As you know, the problem of interference, i.e. interaction of wells, is one of the important tasks in the gas industry. When wells are interfered with, the flow rates and bottom-hole pressures of other wells operating the same reservoir change under the influence of changes in the operating mode of one well. At the same time, the total gas production from the fields with the commissioning of new wells is growing more slowly than the number of wells.
This article considers the interference of an arbitrary number of wells with a remote feed loop, taking into account the influence of the initial pressure gradient.
Key words: interference, interaction of wells, production rate, reservoir initial pressure gradient, gas.
Предположим, в горизонтальном пласте толщиной h работают n скважин с забойным потенциалом 
Для n скважин потенциал в любой точке пласта А определяется формулой [1]:
(1)
Поместив точку А последовательно на забой каждой скважины, получим выражение забойного потенциала для них:
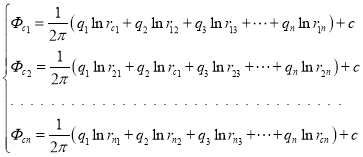(2)
Система (2) состоит из n уравнений и содержит (n+1) неизвестных (n дебита скважин и постоянную интегрирования с).
Дополнительное уравнение получается, если поместить точку А на контур питания:
(3)
Почленно вычитая каждое из уравнений (2) из (3), исключим постоянную с и получим систему из n уравнений, решив которую можно определить дебиты скважин, 
если заданы забойные 
и контурный 
потенциалы.
Влияние начального градиента на фильтрацию флюидов рассмотрена в различных работах [2,3,4,5]. Учитывая, что градиент давления, который тратится на преодоление давления 
, и на начальный градиент давления в призабойной зоне. Зная, что основное снижение давления происходит в призабойной зоне, при 
мы должны подставить, 
Так как 
то 
(4)
После вычитаний и подстановки (4) получаем систему n уравнений в виде:
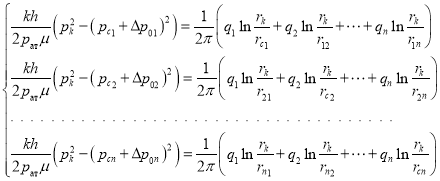(5)
или
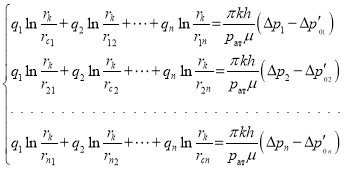(6)
Здесь 
Подставляя нижеуказанные выражения
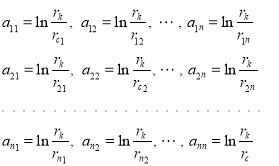(7)
здесь 
в (6) получаем систему n уравнений для определения дебитов 
в виде:
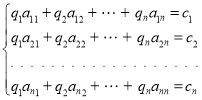(8)
Решение этого уравнения имеет вид:
(9)
где
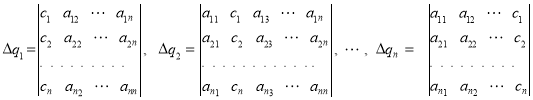(10)
Учитывая (9) и (10) можно получить формулы для дебитов n скважин. Например, для n=2,3 для дебита 
можно получить следующие выражение:
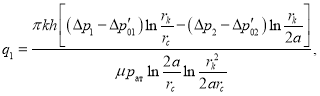(11)
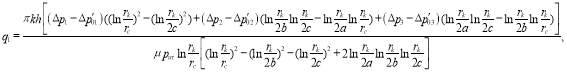(12)
В связи с громоздкостью выражений аналогичные формулы для 
не приводятся.
Таким образом, в статье получены формулы для притока газа к n числу скважин в пласте с удаленным контуром питания с учетом влияния начальных градиентов давлений.
Литература:
- Басниев К. С. Нефтегазовая гидромеханика /К. С. Басниев, Н. М. Дмитриев, Г. Д. Розенберг. — Москва-Ижевск: Институт компьютерных исследований, 2005.
- И. Р. Гасанов, М. А. Джамалбеков. Плоскорадиальный поток несжимаемой жидкости в слоисто-неоднородном пласте с различными начальными градиентами давления. Научно-методический журнал «Вестник науки и образования» № 22 (76), 2019 Ноябрь, с.97–99
- И. Р. Гасанов, М. А. Джамалбеков. Плоскорадиальный поток несжимаемой жидкости в зонально-неоднородном пласте с учетом влияния начального градиента давления. Научно-теоретический журнал «Наука, образование и культура» № 9 (43), 2019 Ноябрь, с.53–55
- И. Р. Гасанов, М. А. Джамалбеков. Плоскорадиальное вытеснение нефти водой с учетом влияния начального градиента давления. Научный журнал «Наука, образование и культура» № 10 (44), 2019 Декабрь, с.11–15.
- И. Р. Гасанов, М. А. Джамалбеков. Обобщенная методика интерпретации данных гидрогазодинамических исследований при нелинейных законах фильтрации с учётом влияния начального градиента. Научно методический журнал «Вестник науки и образования» 2020. No 3 (81). Часть 1. с.97–102.
