В статье предложены формулы для определения градиента давления или депрессии (который должен быть дополнительно преодолен и связан с увеличением скорости фильтрации).
Ключевые слова: градиент, давление, депрессия, фильтрация
The article proposes formulas for determining the pressure gradient or depression (which must be overcome further, and which is associated with an increase in the filtration rate).
Keywords: gradient, pressure, depression, filtration
При разработке залежей при больших градиентах давления на фильтрацию жидкости в пористой среде влияют инерционные силы, которые создают дополнительные сопротивления, направленные против движения. Таким образом, при больших скоростях течения природа нелинейности закона фильтрации иная, чем при малых скоростях фильтрации.
Следует также отметить, что наличие у жидкости релаксационных (неравновесных свойств) определяет характер сопротивления при движении в пористой среде. Течение через сужения и расширения поровых каналов сопровождается деформацией жидких частиц. Поскольку релаксирующая жидкость реагирует на изменение условий с некоторым запаздыванием, то в зависимости от скорости движения характер сопротивления будет меняться. Когда течение достаточно медленное, соответственно медленно происходят деформации жидких частиц, и жидкость успевает реагировать на эти изменения. С увеличением скорости движения время прохождения через сужение уменьшается, и жидкие частицы не успевают деформироваться. Это приводит к увеличению сопротивления движения [1, 2.
В работе определяется давление, которое образуется в связи с влиянием инерционных сил. Как известно, закон Дарси представляется в виде 
, а двучленный закон фильтрации имеет вид [3]:
(1)
Здесь 
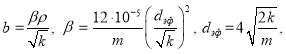(2)
в котором значение b определяется по данным Е. М. Минского [4].
В выражении (2) 
– плотность жидкости, m — пористость породы, d — диаметр зерен, составляющий породу. Определение d, как правило, требует предварительного анализа исследуемой среды и довольно трудоемких экспериментов. В. Н. Щелкачев предложил в качестве линейного параметра d брать величину, пропорциональную корню квадратному из проницаемости. Путем обработки известных экспериментальных данных В.Геертсма [5] показал, что для многих образцов пород 
Эта зависимость удобна тем, что в нее не входит неизвестный параметр d/
По данным Г. М. Ломизе [6, 7]
(3)
Последнее выражение для трещиноватой среды есть результат обобщения зависимости 
полученной Б. Ф. Степочкиным на основе обработки экспериментальных данных для большого диапазона размеров твердых частиц, слагающих продуктивные пласты.
Роль твердых частиц породы в формуле (3) играют блоки, средний линейный размер которых обозначен через 
— поправочный коэффициент по Г. М. Ломизе; m — трещинная пористость, равная отношению объема трещин по всему объему трещиноватой среды.
Существуют и другие менее известные формулы. Все это показывает, что в зависимости от скорости фильтрации значение b изменяется в широком диапазоне. С увеличением скорости значение в формуле (1) члена 
не только становится соизмеримо с членом 
но и становится намного больше. В связи с чем полученное значение скорости фильтрации оказывается меньше, чем по закону Дарси. То есть для скорости фильтрации можно написать следующее выражение:
(4)
Здесь 
— градиент давления, который направлен против движения и связан с влиянием инерционных сил.
После некоторых преобразований из (1) действительно можно получить формулу (4), где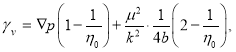 
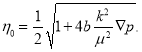(5)
Как видно, градиент инерционного давления
прямо пропорционален 
и обратно пропорционален коэффициенту проницаемости k.
Можно показать, что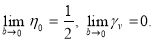 
Следует также отметить, что с уменьшением скорости фильтрации при двучленном законе фильтрации уменьшается и дебит скважины. Если при линейном законе фильтрации для дебита нефти существует формула Дюпи в виде [3]:
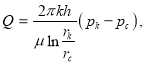(6)
Для идеального газа в виде [3]:
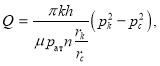(7)
то при двучленном законе можно эти формулы представить в виде:
для нефти —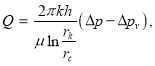 
(8)
где 
для газа —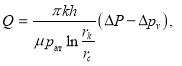 
(9)
Здесь
– давление, которое направлено против движения и связано с влиянием инерционных сил.
А теперь получим формулу для .
Как известно, для дебита нефти при двучленном законе фильтрации существует выражение [3]:
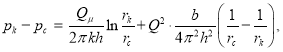(10)
а для газа [3]:
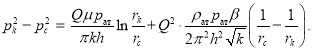(11)
Левую часть в обеих формулах обозначим через 
, и коэффициент при Q и Q2 обозначим соответственно через А и В. Тогда получается выражение в виде:
(12)
Проведем следующие преобразования:
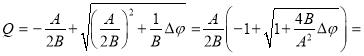
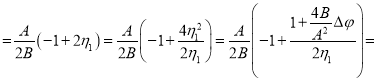
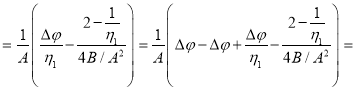
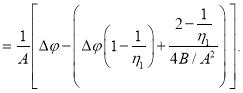
Таким образом,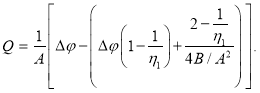 
Здесь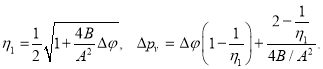 
А теперь покажем, что 
.
Действительно, так как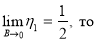 
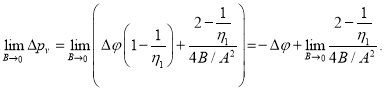
Здесь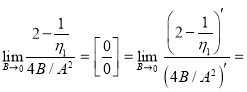 
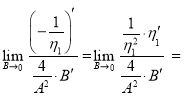
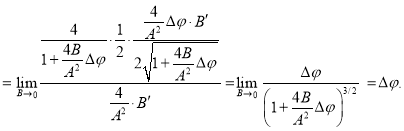
Тогда 
Таким образом, мы для дебита газа получаем формулу:
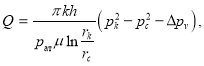
где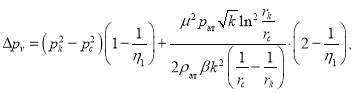 
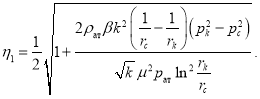
Для дебита нефти эта формула имеет следующий вид:
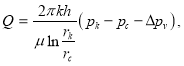
где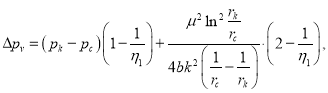 
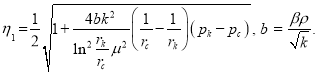
Схематично графический вид 
имеет следующий вид:
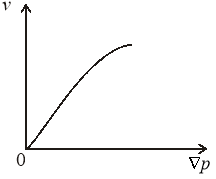
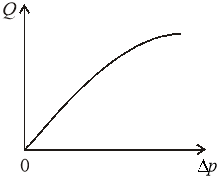
Рис.1. График изменения 
. Рис.2. График изменения 
.
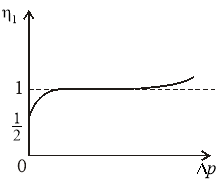
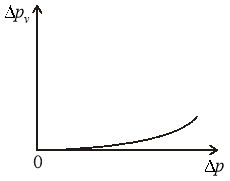
Рис. 3. График изменения 
Рис. 4. График изменения 
Литература:
- А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003. –880 с.
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. –Москва-Ижевск: Институт компьютерных исследований. —2005. –280 с.
- К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. Подземная гидравлика. –М.: Недра, 1986. — 303 с.
- Минский Е. М. О турбулентной фильтрации газа в пористых средах // Тр.ВНИИгаза. –М.: Гостоптехиздат, 1951. –С.64–71.
- Geertsma I. Estimating coefficient of initial resistance in fluid flow through porous media. Sos. Petrol. Engrs J., 1974, X. vol. 14, № 15. p. 445–450.
- Ломизе Г. М. Фильтрация в трещиноватых породах. — М: Госэнергоиздат, 1951.
- Пыхачев Г. Б., Исаев Р. Г. Подземная гидравлика. –М.: Недра, 1973.
