Алгоритм определения неизмеряемых координат объекта управления

В процессе функционирования системы в реальных условиях невозможно измерять некоторые параметры, которые существенно влияют на качества управления. Поэтому при создании высокоэффективных систем управления возникает необходимость восстанавливать значения этих неизмеряемых координат.

Рассмотрим вопрос об определении неизмеряемых координат в процессе работы системы. Пусть заданы дифференциальные уравнения объекта, известны внешние возмущения и последовательность векторов управления. Измеряются с помощью датчиков m>n координат выходного вектора системы. Требуется найти алгоритм для определения (за некоторое минимальное число шагов дискретности) последовательности неизмеряемых координат выходного вектора. Найдем вначале необходимое начальное число шагов дискретности .

Запишем систему уравнений параметров состояния для k =,1,2,3…,:

……………………………………………...

Система уравнений содержит известные матрицы W(T), А₁(Т), С₁(Т) и известные последовательности u(kT), и f [kT].

Выходной вектор системы у(kT)разделим на два вектора: вектор измеряемых выходных координат у_И [kT], в который включим все m координат, измеряемых датчиками, и вектор неизмеряемых координат у_Н [kT], в который включим все остальные n-m координат. В первом уравнении системы число неизвестных выходных координат составит 2(n-m). Во всех последующих (-1) уравнениях число неизвестных координат составит (-1) (n-m).

Таким образом, общее число неизвестных будет определяться формулой

Число уравнений для их определения равно n причем некоторое число уравнений g₀ < n может оказаться лишним. Необходимое число шагов дискретности для определения g неизвестных определяется из равенства

откуда

Для определения необходимого числа шагов дискретности можно воспользоваться также формулой

В случае, если число дробное, то берется ближайшее большое целое . Число лишних уравнений подсчитывается по формуле:

g₀ = (+ 1) n-m.

После начального числа при каждом шаге число неизвестных для следующего шага будет всегда меньше числа уравнений, которые могут быть использованы для их определения, так как m < n. Поэтому только для начального числа шагов . Найдем формулы для вычисления неисчисляемых координат. Преобразуя систему уравнений, получим:

…………………………………………….. (1.1)

Введем в рассмотренные подматрицы W_и(Т) и W_н(Т), которые получаются из матрицы W(Т) по следующему правилу. Подматрица W_и(Т) получается из матрицы W(Т) путем исключения всех j-х столбцов, которые соответствуют номерам неизмеряемых координат. Исключенные столбцы составляют укороченную матрицу W_н(Т). Таким образом, выражение:

с учетом разделения вектора на два вектора можно записать так:

(1.2)

Аналогичную операцию проделаем для единичной матрицы Е типа n x n и будем иметь

(1.3)

Учитывая формулы (2.4) и (2.5), получим выражение для k-го уравнения системы (4.40) в следующем виде:

Объединив координаты векторов и в одни вектор

получим (1.4)

где через L_K обозначена матрица, состоящая из двух клеточных матриц:

L_K = (W_H(T)-E_H).

Совокупность уравнений (1.4) можно записать так:

,

где ,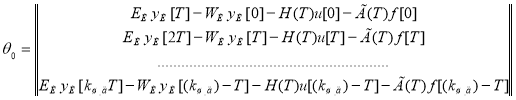

и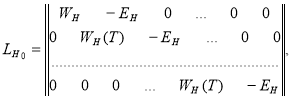

Если , то лишнее число строк матриц и системы, численно равное значению , исключается таким образом, чтобы ранг матрицы , которая получается после исключения строк, был равен числу искомых неизвестных. Получим новую систему

где и — соответственно вектор и матрица, получающиеся при исключении строк. Решение системы запишем в виде

(1.5)

Уравнение параметров состояния для последующих шагов дискретности будет иметь вид

(1.6)

Учитывая формулу (1.5), после преобразований получим

Из системы уравнений (1.6) исключим те строки, в которых матрица F_Н содержит нули, тогда получим рекуррентную систему уравнений для вычисления неизмеряемых координат:

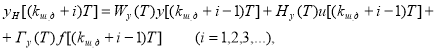(1.7)

где через обозначены усеченные матрицы. Они получаются исключением тех строк матриц , которые соответствуют нулевым строкам матрицы Е_Н.

В качестве модели представления знаний продукционного типа можно взять модель на базе таблиц решений. Структура ядра информационные связи между его компонентами в процессе принятия решений, включая управляемый объект, изображены на рисунке 1.

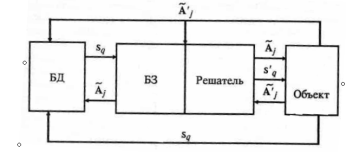
Рис. 1. Структура системы принятия решений

Выделение средств манипулирования знаниями из компоненты представления знаний позволяет создать мощные решатели задач, поддерживающие различные модели представления знаний.

Таким образом, в результате приведенного анализа найдены алгоритмы для определения неизмеряемых выходных координат системы и внешних возмущений в процессе работы системы. Необходимое минимальное начальное число шагов (1.6), а алгоритм для определения обобщенного вектора — формулой (1.7).

Литература:

1. Ж. У. Севинов, Ж. Х. Игамбердыев, А. Х. Абдуганиев, У. Ф. Мамиров. Регуляризованные алгоритмы оценивания векторного параметра в задачах гарантированного оценивания // Журнал «Химическая технология. Контроль и управление», № 6, 2015, стр. 89–92.
2. Х. З. Игамбердиев, А. Х. Расулев, У. Ф. Мамиров Алгоритмы синтеза наблюдающего устройства внешних воздействий в системах управления // МНПК «Современные материалы, техника и технологии в машиностроении», Андижан, с.34–35.