В данной исследовательской работе мы хотим предоставить модель, с помощью которой легко можно будет объяснить свойство некоторых материалов, способных обладать нулевым электрическим сопротивлением, при достижении определенного значения критической температуры, то есть сверхпроводимость. В этой работе мы будем изучать сверхпроводимость определенного материала- двухслойный графен, при повороте его на «магический» угол. Предоставленная нами модель имеет свои определенные особенности: во-первых, в этой модели электроны объединяются в куперовские пары, за счет взаимодействия оптических фононов, во-вторых, происходит уменьшение значения критической температуры графена, причиной данного процесса является кулоновское отталкивание, которое мешает электронам собраться в пары.
Первоначально до того, как приступить к исследовательской работе, давайте охарактеризуем, что из себя представляет графен.
Графен — это двумерная аллотропная модификация углерода, которая образуется слоем атомов углерода толщиной в один атом или монослой графита (основной источник графена).
Графен обладает многими невероятными свойствами, что делает его уникальным материалом, который будет в дальнейшем занимать первое место на всей электронной индустрии.
Одно из главных уникальных свойств графена — линейный закон дисперсии электронов. Если мы пнем ногой по мячу и он приобретет некий импульс, то его энергия будет пропорциональна квадрату импульса. Так же ведут себя мячики-электроны во многих других системах, например в обычном металле. В графене же ввиду особой кристаллической решетки энергия электронов пропорциональна самому импульсу. Схожим законом дисперсии обладают релятивистские частицы, у которых нет массы. Прямое следствие релятивистского закона дисперсии в графене — парадокс Клейна. Это особый вид туннелирования. Обычно квантовые частицы имеют лишь некую вероятность пройти через энергетический барьер. В графене же частицы могут туннелировать абсолютно беспрепятственно.
На сегодняшний день графен представляет собой уникальную платформу для изучения физики низкоразмерных структур. Этим материал обязан совокупности своих уникальных свойств: он самый тонкий, самый прочный и жесткий, самый теплопроводный, обладает самыми легкими носителями заряда с наибольшей длиной свободного пробега среди всех существующих материалов. Графен может выдерживать огромные плотности тока и механические растяжения, является уникальной непроницаемой мембраной, не пропускающей даже атомы гелия. Это лишь краткий список того, почему графен привлек огромную популярность в мире физики конденсированного состояния.
Среди модификаций самого графена в первую очередь стоит отметить двухслойный графен — уникальный объект, который, в отличие от монослоя, обладает запрещенной зоной. Благодаря этому двухслойный графен гораздо более пригоден для создания транзисторов: именно запрещенная зона определяет возможность перевести транзистор в непроводящее состояние, то есть выключить.
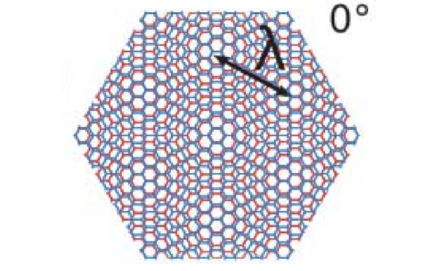
Рис. 1. Муарова сверхрешетка, образованная при наложении двух материалов
Уникальные свойства данного материала, то есть двухслойного графена, обнаружили не так давно. Это произошло под руководством Пабло Харильо-Эрреро, в марте 2018 года. Группа ученых с Пабло выяснили, что данный вид графена, который обладает запрещенной зоной становится сверхпроводником, при определенных условиях. Например, при повороте его на «магический», а если быть точным, угол, при котором скорость Ферми в материале падает до нуля.В нашем случае исследуемый материал имеет несколько таких «магических» углов. При этом первый «магический» угол двухслойного графена близок к 1,1 градуса, критическая температура составляет примерно 1,7 К.
Открытие данного свойства двухслойного графена, как сверхпроводимость стало очень величайшим событием, несмотря на то, что до этого момента ученым были известны и другие, не менее, уникальные свойства данного материала.
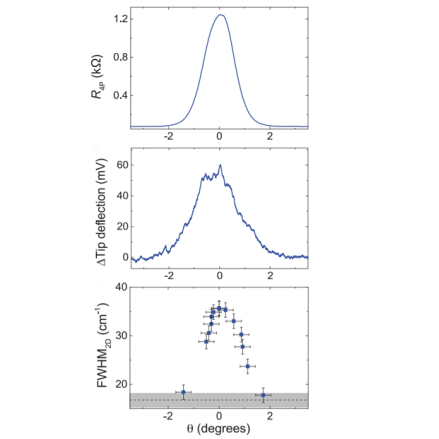
Рис. 2. Изменение электрического сопротивления, уровня отклонения кантилевера и полуширины 2D-пика рамановского рассеяния в зависимости от угла между плоскостями
В предложенной нами модели, как и в обычных сверхпроводниках, данное свойство возникает за счет электронного взаимодействия, связывающее их в куперовские пары и позволяющее преобразовать, за счет обусловленного сотрудничества бозе-конденсаты. Следует отметить, что создание данной модели несколько отличается от обычной сверхпроводимости.
В основу механизма преобразования связанных электронов, путем их взаимного притягивания, лежит муаровый гамильтониан, описывающий количество энергии электронов и квазичастиц, которые распространяются в двухслойном графене. Для полного описания данного гамильтониана необходимо учесть следующее: движение электронов в верхнем и нижнем слоях, а также туннелирование между ними. Своё название он получил из-за муарового узора, образующий тонкие листы графена или графита, при повороте на угол θ. Данный узор может быть описан треугольной решёткой, постоянная которой в 1/2sin(θ/2) раз больше постоянной исходной шестиугольной решётки листов графена. Используя свойства этой решетки и исходя из данного отношения, можно с легкостью рассчитать зонную структуру конечного проводника, получившийся из эксперимента. Имея результаты рассчитанных топологических свойств системы и основ структуры, можно однозначно утверждать, что она сильно зависит от угла θ. Неподалеку от самого «магического» угла количественно-энергетические зоны становятся плоскими, плотность состояний взаимосвязанных электронов растет, и уже взаимодействием частиц нельзя ни в коем случае пренебрегать. При этом если мы будем рассматривать каждую энергетическую зону по отдельности, то здесь различаются существенные различия энергии и импульсов электронов. Исходя из этого образование куперовских пар в пределах определенной зоны невыгодно, а поэтому мы берем общее образование, учитывая связь между их свойствами и недостатками.
Наряду с рассмотрением электронного взаимодействия, были взяты под наблюдение несколько фононных мод, которые возникают в двухслойном графене. Оказалось, что наибольший эффект связан с оптическими фононами, описывающие колебания атомов, не согласованные по фазе, то есть электроны движутся в противоположные стороны. Вычисляя гамильтониан взаимодействия по фононным модам, учёные рассчитали вероятность образования пар, с учетом их зависимости от энергии и суммарного потенциала фононных частиц. Возможность интенсивности характера образования данных пар зависит от рассеяния частиц в s-волне (суммарный угловой момент пары L = 0) с критической температурой 10 К, и d-волне (L = 1), температура равна 3 К.С учетом этого, исследуемая система находится в режиме сильной связи, константа взаимодействия, описывающая состояние электронов приблизительно равна единице.
На основе всего этого, можно сказать, что данные эксперимента противоречат теории, в которой отмечалось, что максимальная температура взаимодействия электронов и фононов сверхпроводимости не превышает 2 К. Исходя из вышесказанного, следует заметить, что данная структура двухслойного графена обладает электронно-дырочной ассиметрией, поэтому сама теория данного материала очень чутко относится к выявлению новых параметров и свойств.
В данной исследовательской работе мы рассмотрели модель электронного и фононного взаимодействий. Первый тип взаимодействия приводит к образованию куперовских пар через рассеяние в s-волне, второй — в d-волне. С помощью подборки количества в каждой экспериментальной зоне, нам удалось приблизиться к воспроизведению экспериментальных данных. Поэтому следует полагать, что теория описывает абсолютно четко происходящие процессы в двухслойном графене, которые могут быть отслежены, в ходе проведения экспериментов.
Литература:
- Адамсон А. Физическая химия поверхности. М.: Мир 1979.
- Денисова Л. Г. Интенсивная методика характерики графена. — ИЯШ, 1989, № 2, с 47–49.
- D. Marchenko, D. V. Evtushinsky, E. Golias, A. Varykhalov, Th. Seyller, O. Rader. Extremely flat band in bilayer grapheme.
- Функциональные наполнители для полимеров. / Под ред. М. Ксантоса. Пер. с англ. Кулезнева В. Н. — СПб: Научные основы и технологии, 2010–462 с.
- G. Alymov, V. Vyurkov, V. Ryzhii, D. Svintsov, Abrupt current switching in graphene bilayer tunnel transistors enabled by van Hove singularities. Sci. Rep. 6, 24654 (2016).

