Эволюционные алгоритмы широко применяются на этапе конструирования мобильных роботов. В результате работы алгоритмов создаются файлы с моделями. Модель представляет собой структуру мобильного робота, которая описывается с двух точек зрения: с точки зрения кинематической структуры, с точки зрения системы управления.
- описание кинематической схемы:
- кинематические связи между элементами;
- физические параметры элементов;
- геометрия элементов;
- положение элемента в пространстве.
- описание системы управления:
- набор управляющих элементов и операторов;
- связи между управляющими элементами (логика алгоритма управления).
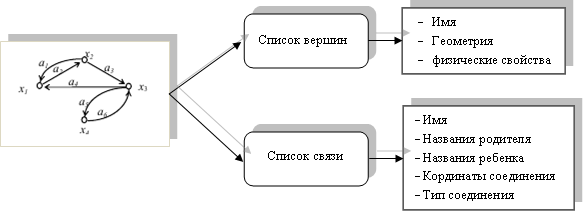
Кинематическая схема - множество элементов, которые изображают форму модели робота, каждый кинематический элемент содержит имя, геометрию, физические свойства и свое положение в пространстве, кинематическая схема - связь между этими элементами.
Система управления - набор управляющих элементов (датчик, управляющий агрегат и исполнительные механизмы), каждый управляющий элемент содержит кинематическую схему и их сигналы (вход, выход, переменные, параметры), которые обрабатываются алгоритмами поведения робота.
Для описания элемента роботов каждый элемент содержит имя, геометрию, размер, физические свойства и свое положение в пространстве.
- геометрия элемента может быть многогранником, прямой, эллиптическим цилиндром, эллипсоидом, шаром и т.д.;
- размер элемента – это масштаб элемента (общий масштаб и частичный масштаб по осям);
- физические свойства элементов включают размер, массу элементов и т.д.;
- положения элементов в пространстве включают центральные координаты и угол вращения по осям.
Элементы мобильного робота включают форму, колеса, датчик, микроконтроллер, исполнительные механизмы и т.д.
Проанализировав системы, эволюционно установлено, что в модели робота существуют избыточные компоненты, что приводит к следующим недостаткам:
- отсутсвие средств анализа моделей;
- большие временные затраты для анализа модели;
- неудобство визуализации модели в пространстве.
Таким образом, необходимо разработать собственную систему для оптимизации моделей, полученных в результате работы эволюционных методов. В этой системе необходимо использовать методы оптимизации для повышения эффективности работы системы эволюционного моделирования:
- разработка подсистемы анализа моделей;
- минимизация количества вершин и связей;
- минимизация площади изображения;
- минимизация вершин, влияние которых на выходные значения не превышает заданной погрешности.
В результате работы был написан модуль, позволяющий:
- визуализировать модели мобильных роботов на графе;
- осуществлять "слепые" вершины (т.е. вершины, не имеющие путей к выходным вершинам);
- отсечь вершины, влияние которых на выходные значения не превышает заданной погрешности.
Разработка модуля оптимизации модели мобильных роботов
В процессе автоматизированного синтеза система выполняет три главные функции: оптимицация модели робота, визуализация модели мобильных роботов, сохранение файла после оптимизации.
В системе реализованы следующие основные функции:
- Оптимицация модели робота
- отсечение маловажных вершин – вершины, не имеющие путей к выходным вершинам;
- отсечение вершин, влияние которых на выходные значения не превышает заданной погрешности.
- Визуализация модели мобильных роботов
- изображение на 2Д-графике модели робота с характеристиками и изображенями и связи между ними;
- изображение на матрице смежности количества связей между двумя моделями;
- изображение на матрице инциденций направления связей.
Визуализация модели мобильных роботов на графе
При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.
Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.
Визуализация или отображение графов, как ответвление теории графов, относящееся к топологии и геометрии — двумерное представление графа. В основном, это графическое представление укладки графа на плоскость (как правило, допускаются пересечение рёбер), направленное, обычно, на удобное отображение некоторых свойств графа, или моделируемого объекта.
Вершина — базовое понятие: объект, где могут сходиться/выходить рёбра. Множество вершин графа G обозначается V(G). В этой системе, вершина это элемент роботов, включающие параметры, физический размер.
Ребер — базовое понятие. Ребро соединяет две вершины графа. В этой случие, ребер это связи между элементами (присоединения координаты), результаты присоединения.
Система должна прочитать из исходных файлов список вершин и список связей, такие списки бузят изображаться на матрице смежности и на матрице инциденций, после этого система должна расположить вершины и связи на графе.
Визуализация графов отображает связи между элементами роботов, т.е. на графе должен описать элементы роботов, включающие параметры, физический размер и связи между элементами — результаты присоединения.
Рисунок 2 - Структура описания визуализация графов
- Для визуализации графов необходимо узнать:
- количество связей между двумя моделями;
- направление связей.
П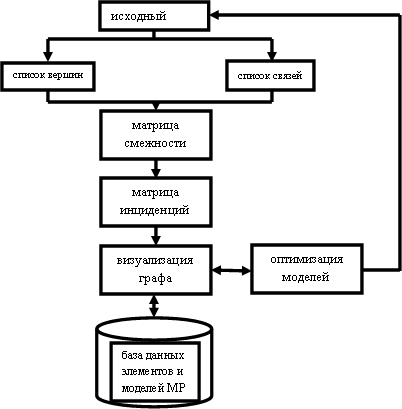 ри
решении этой задачи
используются следующие способы описания графа: матрица ициденций,
матрица смежности.
ри
решении этой задачи
используются следующие способы описания графа: матрица ициденций,
матрица смежности.
Графы, как правило, отображаются графически при помощи точек для представления вершин и отрезков, или ломаных, для отображения рёбер между связанными вершинами. Ориентация ребра отображается при помощи стрелки. Для каждого графа существует множество различных способов его отображения. Более конкретно, важно расположение этих вершин и рёбер, удобство восприятия, использования, стоимость создания и эстетические критерии.
Рисунок 3 – Подсистема визуализация графов
Оптимизации модели робота
Оптимизация — процесс нахождения наилучшего решения какой-либо задачи при заданных условиях, ограничениях и критериях.
В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значения параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической. Задача выбора оптимальной структуры является структурной оптимизацией.
Оптимизационные задачи широко распространены в экономике, технике, информатике и в других сферах. Особенностью оптимизационных задач является предположение о наличии некоторого (оптимального) решения, при отклонении от которого в ту или иную сторону некоторые показатели могут улучшаться, некоторые — ухудшаться, но в целом «качество» решения ухудшается.
Дан ориентированный граф G, множество вершин которого V и множество рёбер - E. Петли и кратные рёбра допускаются. Обозначим через n количество вершин графа, через m - количество рёбер. Требуется найти все пути между двумя заданными вершинами и отсечение вершин не имеющих путей к выходным вершинам.
Как известно, выбор критерий оптимальности имеет важное значение. При решении этой задачи можно производиться по различным критериям оптимальности в зависимости от цели, мы исследовали о технических критериях, эстетических критериях и др. Исходя из этого, чтобы соответствовать требованиям этой задачи, мы выбрали следующие критерии:
- минимизации избыточных компонентов, которые не имеющих путей к выходным компонентам;
- минимизация компонент, влияние которых на выходные значения не превышает заданной погрешности;
- минимизация площади изображения.
В соответствии с этими критериями модуль оптимизации модели робота необходимо осушествовать следующие функции:
-
отсечение
"слепых" вершин
 вершины не имеющих путей к выходным вершинам;
вершины не имеющих путей к выходным вершинам;
- отсечение вершин, влияние которых на выходные значения не превышает задоной погрешности.
Метод
отсечения
"слепых" вершин
![]() эта процедура нахождения всех путей между двумя заданными вершинами.
Мы используем алгоритм поиска в ширину (обход в ширину, breadth-first
search) — это один из основных алгоритмов на графах.
эта процедура нахождения всех путей между двумя заданными вершинами.
Мы используем алгоритм поиска в ширину (обход в ширину, breadth-first
search) — это один из основных алгоритмов на графах.
Алгоритм работает за O(n + m), где n— число вершин, m— число рёбер.
На вход алгоритма подаётся заданный граф, и номер стартовой вершины s. Граф может быть как ориентированным, так и неориентированным, для алгоритма это не важно.
Сам алгоритм можно понимать как процесс "поджигания" графа: на нулевом шаге поджигаем только вершину s. На каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей; т.е. за одну итерацию алгоритма происходит расширение "кольца огня" в ширину на единицу (отсюда и название алгоритма).
Более
строго это можно представить следующим образом. Создадим очередь
![]() ,
в которую будут помещаться горящие вершины, а также заведём булевский
массив used[],
в котором для каждой вершины будем отмечать, горит она уже или нет
(или иными словами, была ли она посещена).
,
в которую будут помещаться горящие вершины, а также заведём булевский
массив used[],
в котором для каждой вершины будем отмечать, горит она уже или нет
(или иными словами, была ли она посещена).
Изначально
в очередь помещается только вершина
![]() ,
и used[s]
= true,
а для всех остальных вершин used[s]
= false.
Затем алгоритм представляет собой цикл: пока очередь не пуста,
достать из её головы одну вершину, просмотреть все рёбра, исходящие
из этой вершины, и если какие-то из просмотренных вершин ещё не
горят, то поджечь их и поместить в конец очереди.
,
и used[s]
= true,
а для всех остальных вершин used[s]
= false.
Затем алгоритм представляет собой цикл: пока очередь не пуста,
достать из её головы одну вершину, просмотреть все рёбра, исходящие
из этой вершины, и если какие-то из просмотренных вершин ещё не
горят, то поджечь их и поместить в конец очереди.
В результате поиска в ширину находится все пути между двумя заданными вершинами в ориентированом графе.
|
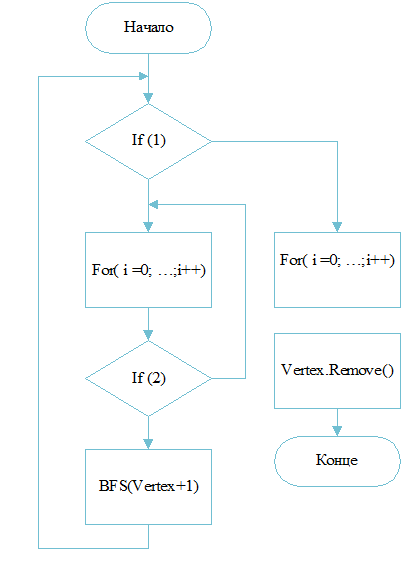
Рисунок 4 – Метод отсечение "слепых" вершин
Литература:
- Робототехнтка [Электронный ресурс]. – 2006. – Режим доступа: http://www.prorobot.ru/12/robot-it-is.php
- Робот [Электронный ресурс]. – 2008. – Режим доступа: http://ru.wikipedia.org/wiki/%D0%A0%D0%BE%D0%B1%D0%BE%D1%82
- Робот для программиста [Электронный ресурс]. – 2007. – Режим доступа: http://robot.paccbet.ru/robot_for_programmer.php.htm
- Алгоритм поиска пути для роботов [Электронный ресурс]. – 2007. – Режим доступа: http://robot.paccbet.ru/robot_path.php.htm
- Финн, В. К. Правдоподобные выводы и правдоподобные рассуждения / В.К.Финн. – М.: ВИНИТИ, 1988. - Т. 28. – 180 с. – (Итоги науки и техники. Сер. «Теория вероятностей. Математическая статистика. Теоретическая кибернетика»).
- Искусственный интеллект. В 3 т. Т. 2. Модели и методы: справочник/ под ред. Д. А. Поспелова. – М.: Радио и связь, 1990. – 304 с.