В дошкольном возрасте происходит всестороннее развитие детей: у них формируются психические познавательные процессы и элементарные математические представления, развиваются мыслительные операции и сенсорная культура, они учатся обследовать предметы и наблюдать за явлениями, называть их признаки и выделять характерные особенности, познают окружающий природный и социальный мир [3, с. 235].
Всестороннее развитие детей в перспективе будет способствовать формированию и становлению самодостаточной, успешной, креативной и инициативной личности, обладающей развитыми волевыми качествами.
В связи с этим, в дошкольном образовании акцент делается на формировании и развитии творческого потенциала и познавательно-исследовательской активности детей в различных видах деятельности [1].
Умелое овладение знаниями, умениями и навыками, необходимыми для выполнения деятельности, обеспечивается развитием умственных способностей, выступающих ядром познавательного развития.
Познавательное развитие не теряет свою актуальность во все времена. Оно предполагает формирование интеллектуальной сферы, развитие познавательного интереса и активности, расширение кругозора.
Одним из средств познавательного развития детей выступает игра в шахматы. Благодаря этой игре происходит не только формирование психических познавательных процессов (произвольной памяти и произвольного внимания, мышления), умения ориентироваться на плоскости, сравнивать, обобщать, предвидеть результаты своей деятельности и учитывать будущее поведение других людей, становиться на их точку зрения, но и совершенствуются такие качества, как самостоятельность, изобретательность, гибкость, усидчивость, развивается способность «действовать в уме». Способность «действовать в уме» объединяет воображение, внимание, память, мышление, дает человеку возможность оперировать в мысленном плане с заместителями реальных предметов [4, с. 1–3].
Чем раньше научить ребенка игре в шахматы, тем лучше для его дальнейшего обучения (в школе, ВУЗе) и развития в целом. При этом следует помнить слова Л. В. Выготского, который писал, что «обучение должно идти на один шаг впереди развития, вести его за собой» [2, с. 5]
Чему же могут научить шахматы и как это происходит?
Во-первых, при знакомстве с шахматной доской дети дошкольного возраста знакомятся с понятиями «Горизонталь» (рис.1), «Вертикаль» (рис.2), «Диагональ» (рис.3), «Центр» (рис.4); закрепляют понятие «Квадрат»; учатся ориентироваться на шахматной доске; считают количество полей в горизонтали, вертикали, большой и малой диагоналях, количество диагоналей в целом и черных и белых диагоналей по отдельности.
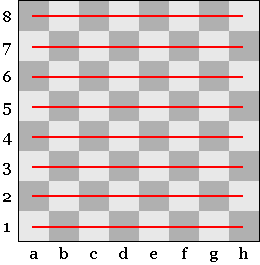
Рис. 1. Горизонтали
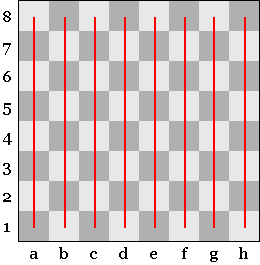
Рис. 2. Вертикали
Объясняем детям, что в горизонталях соседние клетки соединяются боковыми сторонами, в вертикалях — верхней и нижней сторонами.
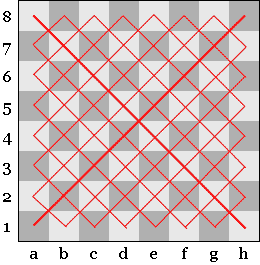
Рис. 3. Диагонали
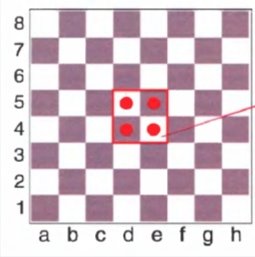
Рис. 4. Центр
Отмечаем, что в диагоналях клетки соединяются противоположными углами. Объясняем, что шахматные диагонали бывают белые и чёрные. Диагонали разные по длине. Бывают совсем маленькие. Диагональ, проведённая из угла в угол, называется большой диагональю. Говорим детям, что есть большая белая диагональ и большая черная диагональ.
Кроме того, с помощью шахматной доски можно закрепить понятие четности и нечетности, которые связаны с номером хода, симметрии, геометрии, но эти понятия подходят для обсуждения с детьми школьного возраста и старше [5, с. 27].
Во-вторых, сопровождение обучения введением сказочных героев, чтением сказок, легенд и других историй про игру в шахматы, появление шахматных фигур делает занятия интересными и увлекательными — дети могут фантазировать, воображать себя «шахматными персонажами», сочинять истории.
В-третьих, знание ходов фигур дает возможность просчитывать ситуацию на несколько ходов вперед (способность «действовать в уме»), оценивать точку зрения и поведение противника, развивает бдительность, гибкость, изобретательность. При совершении хода противником, другой игрок должен предусмотреть его дальнейшие действия, оценить, есть ли, и если да, то какие фигуры «под боем», есть ли угроза королю, какую фигуру можно подставить «под бой» и т. д. [6, с. 16].
Таким образом, у тех, кто играет в шахматы, развиваются внимание, усидчивость, упорство, логическое мышление и стремление решить поставленную задачу при помощи разума.
Литература:
- Аксенова Т. А. Развитие дошкольника в познавательско-исследовательской деятельности в условиях реализации ФГОС ДО // Молодой ученый. — 2016. — № 12.6. — С. 1–6. — URL https://moluch.ru/archive/116/31981.
- Волков Б. С. Психология детей от рождения до трех лет в вопросах и ответах. — ООО «ТЦ «Сфера», 2015. — 128 с.
- Гусова А. Д. Особенности развития познавательных процессов детей старшего дошкольного возраста // Современные исследования социальных проблем. — 2017. — № 6–2. — С.233–240.
- Сухин И. Г. Программы курса «Шахматы — школе: Для начальных классов общеобразовательных учреждений». — Обнинск: Духовное возрождение, — 2011. -40 с.
- Сухин И. Шахматы, первый год, или Там клетки черно-белые чудес и тайн полны: Учебник для 1 класса четырёхлетней и трёхлетней начальной школы. — Обнинск: Духовное возрождение, 1998.
- Сухин И. Шахматы, первый год, или Учусь и учу: Пособие для учителя — Обнинск: Духовное возрождение, 1999.







