Дифференциальные уравнения играют огромную роль в современном мире. Благодаря им, осуществляется движение городского транспорта, а международные компании могут экономить миллиарды долларов на оптимизации своего бизнеса, благодаря тому, что решат нужное дифференциальное уравнение. Нет такой области в современном мире, где не использовались бы уравнения. Однако найти аналитическое решение дифференциального уравнения не всегда возможно, поэтому существует огромное количество классических численных методов для решения данных уравнений (метод Эйлера, метод Рунге-Кутты, метод конечных разностей, конечных элементов, метод Монте-Карло) [1]. Данные методы, либо обеспечивают нужную точность вычислений при этом, расходуют слишком много временных ресурсов, либо работают достаточно быстро, но при этом не обеспечивают необходимую точность. Поэтому сейчас разрабатываются новые численные методы для решения дифференциальных уравнений, на основе нейронных сетей [2, 3, 4].
В данной работе мы рассмотрим численное решение дифференциального уравнения Лапласа с помощью нейронной сети прямого распространения и сравним точность результатов с методом конечных разностей [5, 6].
Постановка задачи. Будем рассматривать обыкновенные и в частных производных дифференциальные уравнения до второго порядка вида:
(1)
Здесь, 
, 
, 
— скалярная функция, решение дифференциального уравнения (1).
Обозначим 
— решение дифференциального уравнения с помощью нейронной сети, p — параметры нейронной сети (веса и смещение), а также дискретизируем нашу область 
. Перепишем уравнение (1) с новыми обозначениями:
.
Теперь запишем функцию минимума ошибки:
(2)
Где,
пробное решение дифференциально уравнения в частных производных. Рассмотрим пробное решение уравнения (1):
(3)
Первое слагаемое удовлетворяет начальным и граничным условиям уравнения (1), функция 
принимает нулевое значение на границе области, 
граница области , 
— функция выхода нейронной сети. Оптимальное пробное решение 
, где 
.
Задача решения дифференциального уравнения (1) заключается в минимизации уравнения (2).
Нейронная сеть. Вданном исследовании используется трёхслойная нейронная сеть прямого распространения, представленная на рис. 1.
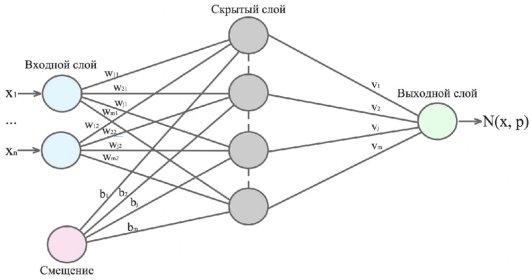
Рис. 1. Архитектура нейронной сети
Входной слой состоит из 
элементов и смещения, — размерность вектора 
(на входной слой подаются координаты вектора ), скрытый слой состоит из 
элементов. Количество элементов в скрытом слое определяется экспериментально. Выходной слой состоит из одного элемента, он представляет собой сумматорную функцию (4)
(4)
Нейронная сеть обучается методом обратного распространения ошибки с использованием градиентного метода с постоянным шагом. В качестве активационной функции скрытого слоя используется сигмоида. Задача обучения нейронной сети заключается в поиске весов 
для минимизации уравнения (2).
Основная идея метода. Главная идея заключается в замене каждого 
из тренировочного множества на многочлен вида 
, 
. Тогда вектор входных значений будет иметь вид: 
Данное преобразование позволяет выбирать точки не учитывая начальные и граничные точки, тем самым можно снизить вычислительную ошибку.
Пример. Рассмотрим дифференциальное уравнение Лапласа
|
|
где 
, 
. Начальные и граничные условия 
, 
, 
, 
.
Запишем аналитическое решение, чтобы можно было сравнивать результаты:
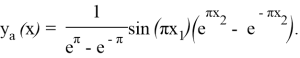
Уравнение (3) для данного примера будет выглядеть:
Необходимо записать функцию минимума ошибки для уравнения Лапласа:
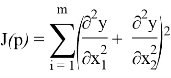
Результаты вычислений. В таблице 1 представлены результаты вычислений для нейронной сети и метода конечных разностей. Для вычислений методом конечных разностей квадратная область разбивалась на 121 элемент [7].
Таблица 1
Результаты вычислений для нейронных сетей иметода конечных разностей
|
|
Нейронная сеть |
Конечн. разностей |
|
Максимальное отклонение |
0.06150599166 |
0.056468425 |
|
Среднее отклонение |
0.000962346874 |
0.00798621684 |
|
Сумма отклонений |
0.112678654 |
80.3214654246 |
Заключение. Вданной работе было произведено сравнение методов решений дифференциального уравнения Лапласа модифицированной нейронной сетью (модификация входных данных) и метода конечных разностей. Из результатов видно, что нейронная сеть считает точнее по сравнению с методом конечных разностей. Необходимо также заметить что что алгоритм нейронной сети является простым и вычислительно эффективным.
Литература:
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. Изд. 4-е. М.: Бином, 2016. 636 с.
- Kagan E. and Ben-Gal I. A Group-Testing Algorithm with Online Informational Machine Learning // IIE Transactions, 2014, Vol.5 No. 4, pp.164–184.
- Montreda C., Saloma C., Charactering the dynamic of constrained physical systems with unsupervised neural network. 1998 // Phys. Rev., E57: pp. 1247–1250
- Ricky T. Q. Chen, Rubanova Y., Bettencourt J., Duvenaud D., Neural ordinary differential equations [Электронный ресурс]: URL: https://arxiv.org/abs/1806.07366v4 (дата обращения: 03.03.2019)
- Н. И. Глебов, Ю. А. Кочетов, А. В. Плясунов. Методы оптимизации. Изд-во НГУ, 2000, 105 с.
- Tsay, R. S. Analysis of Financial Time Series. 3rd ed. Hoboken, NJ: John Wiley & Sons, Inc., 2010 P.365.
- Kai-Li Wang, Fawson C., Modeling Asian Stock Returns with a More General Parametric GARCH Specification // Journal of Financial Studies Vol.9 No.3, pp. 21–52.
