В статье рассматривается алгоритм метода Гаусса для решения систем линейных алгебраических уравнений. Выбран язык Maple, как наиболее оптимальный для реализации алгоритма. В статье содержится листинг программного кода.
Ключевые слова: система линейных алгебраических уравнений, метод Гаусса, алгоритм реализации метода Гаусса, прямой и обратный ход, программный код.
В прикладных задачах довольно часто приходится решать системы линейных алгебраических уравнений (СЛАУ). Это не удивительно, поскольку математические модели тех или иных процессов либо сразу строятся как СЛАУ, либо сводятся к таковым посредством дискретизации или линеаризации.
Метод Гаусса прекрасно подходит для решения СЛАУ. Являясь наиболее мощным и универсальным инструментом для нахождения решения СЛАУ, он обладает рядом преимуществ: 1) нет необходимости предварительно исследовать систему уравнений на совместность; 2) методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю; 3) метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.
Но главное, что было отмечено в работе «Метод Гаусса в школе» М. Ю. Шонина и Л. А. Мамедалиной, «Метод Гаусса решения СЛАУ с числовыми коэффициентами в силу простоты и однотипности выполняемых операций пригоден для счета на электронно-вычислительных машинах» [3].
Настоящая статья посвящена составлению и апробации алгоритма численного решения СЛАУ в соответствии с алгоритмом метода Гаусса. Рассмотрим следующую задачу.
Задача. Решить систему линейных алгебраических уравнений [1]
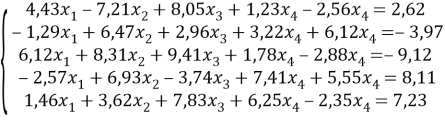
Решение:
Для численного решения СЛАУ воспользуемся математическим пакетом Maple 15. В соответствии с условием задачи имеем:
 и
и 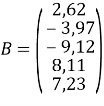
![]()
Для эффективной работы в ![]() необходимо разбираться в тонкостях языка. К ним относится, например, команда
необходимо разбираться в тонкостях языка. К ним относится, например, команда ![]() и переменная
и переменная ![]() .
.
Команда ![]() — очищает память
— очищает память ![]() . Это означает, что все определенные для этого в программе переменные и другие объекты будут стерты. При этом текст программы останется неизменным. Данная функция необходима для осуществления компиляции.
. Это означает, что все определенные для этого в программе переменные и другие объекты будут стерты. При этом текст программы останется неизменным. Данная функция необходима для осуществления компиляции.
Переменная ![]() возвращает необходимое количество знаков после запятой
возвращает необходимое количество знаков после запятой ![]() . Установим точность вычисления
. Установим точность вычисления ![]() . Поскольку нам придется иметь дело с матрицей и вектор-столбцом, то необходимо подключить библиотеку линейной алгебры —
. Поскольку нам придется иметь дело с матрицей и вектор-столбцом, то необходимо подключить библиотеку линейной алгебры — ![]() . Введем данные в программу.
. Введем данные в программу.
> ![]()
> ![]()
> ![]()
![]()
> 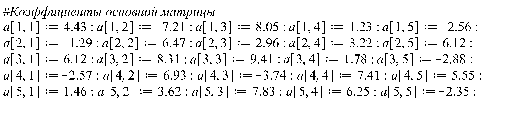
> ![]()
>
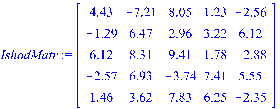
> ![]()

В соответствии с логикой метода Гаусса, программа должна привести матрицу ![]() к треугольному виду (Прямой ход). Целесообразно воспользоваться циклом со счетчиком
к треугольному виду (Прямой ход). Целесообразно воспользоваться циклом со счетчиком ![]() . Цикл
. Цикл ![]() предназначен для реализации итерационных (повторяющихся) действий [2].
предназначен для реализации итерационных (повторяющихся) действий [2].
> 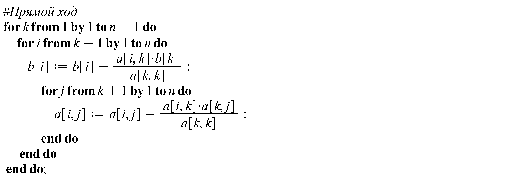
> 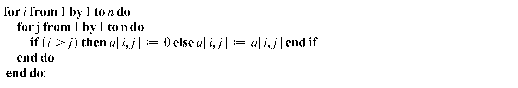
> ![]()
![]()

> ![]()
> ![]()
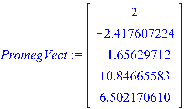
Следующий этап — обратный ход, построчное вычисление входящих в систему переменных и их вывод на экран.
> ![]()
> 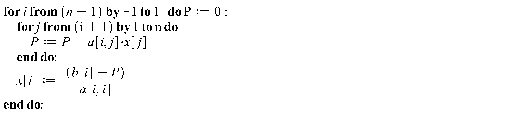
> ![]()

Заключительным этапом программы служит проверка адекватности найденного решения. Для этого воспользуемся командой решения СЛАУ — ![]() .
.
> ![]()

Найдем абсолютную погрешность (модуль разности значений переменных, полученных путем численного решения и при помощи встроенной команды соответственно). Команда ![]() выполняет операции над матрицами. Команда
выполняет операции над матрицами. Команда ![]() возвращает абсолютные значения.
возвращает абсолютные значения.
> ![]()
Анализируя последние результаты, можно констатировать высокую точность вычисления. Таким образом, разработанная программа вполне адекватна для решения СЛАУ.
Литература:
- Ильин В. А. Линейная алгебра: Учебник для вузов / В. А. Ильин, Э. Г. Позняк. — 6-е изд., стер. — М.: Физматлит, 2004. — 280 с.
- Кирсанов М. Н. Практика программирования в системе Maple. — М.: Издательский дом МЭИ, 2011. — 208 с.
- Мамедалина Л. А. Метод Гаусса в решении СЛАУ в школе / Л. А. Мамедалина, М. Ю. Шонин // Весенний школьный марафон: материалы III Междунар. науч.-практ. конф. школьников (Чебоксары, 31 мая 2016 г.) / редкол.: О. Н. Широков [и др.] — Чебоксары: ЦНС «Интерактив плюс», 2016. — С. 139–143.







