В нынешнее время довольно часто встречаются фотографии, эпизоды из кинематографа, здания, изображения, при виде которых можно воскликнуть «Такого не может быть!». Это и рисунки с искаженной перспективой, и невозможные в нашем трехмерном мире объекты, и немыслимые сочетания вполне реальных предметов. Появившись в начале XI века, такие «странные» рисунки и фотографии сегодня стали целым направлением искусства и архитектуры. Так же школьном курсе изучаются выпуклые и невыпуклые многогранники. В кабинете математики есть невыпуклый многогранник, который называется Флексор Штеффена, данный многогранник создан руками ученика, окончившего нашу школу, и поэтому, увидев данный многогранник, я поставила себе цель, а существуют ли еще многогранники и другие невозможные фигуры, которые можно создать своими руками. [1]
Многогранник (многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело), а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника [2]. (приложение 1)
До сих пор не существует чёткого определения невозможных фигур. [3].
Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры.
Невозможные фигуры — это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией. [2] Невозможные фигуры представлены на Рисунке 1
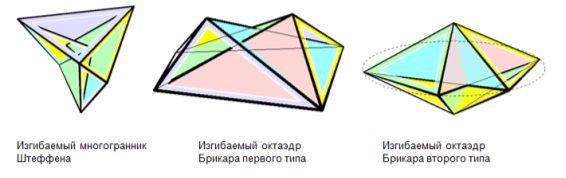
Рис. 1. Изгибаемые многогранники
Невозможные фигуры были известны ещё в Средневековье, но систематическое их изучение началось лишь в середине XX века. Создателями невозможных фигур называют Оскара Реутерсварда и Роджера Пенроуза [2].
При проецировании трехмерной фигуры на плоскость некоторые линии могут становиться невидимыми, перекрывать друг друга. В качестве примера можно взять знаменитый треугольник Пенроуза, Таблица 1
Таблица 1
Создание треугольник Пенроуза
|
Примечание: |
Результат |
|
Предположим, что треугольник Пенроуза можно создать из обычных трёх брусков бумаги |
|
|
В ходе эксперимента было получено 3 одинаковых бруска из обычной бумаги А4. В ходе склеивания модели, бумага потерпело искажение, тем самым произошло нарушение граней. Вывод: Невозможно создать треугольник Пенроуза из обычных равных брусков |
|
|
Но! Треугольник Пенроуза можно создать, если учесть особенность построения фигуры, и согласно определению, линии, невидимые глазу можно исказить. При таком условии, треугольник Пенроуза можно сделать в объёме |
|
Многие люди думают, что невозможные фигуры действительно невозможны, и их нельзя увидеть в реальном мире. На самом деле их можно увидеть в реальности. Надо помнить, что любой рисунок на листе бумаги — это проекция трехмерной фигуры. Следовательно, любая фигура, нарисованная на листе бумаги должна существовать в трехмерном пространстве [4].
Конечно, ни одну из невозможных фигур нельзя создать, действуя прямолинейно. Но можно взять три различных бруска и составить треугольник, представленный на Рисунке 2 [4].

Рис. 2. Треугольник Пенроуза
В зеркале мы видим реальную фигуру. Получается, что приведенная фигура выглядит невозможным треугольником только с единственной точки зрения. Это касается всех невозможных фигур [4].
Области применения невозможных фигур разнообразно. В современном мире они окружают нас практически повсюду. Применение невозможных фигур представлены в Таблице 2.
Таблица 2
Области применения невозможных фигур
|
Область применения |
Изображение |
|
В Иконописи: Христианство очень редко использовало модели несуществующих фигур, но их изображения часто встречаются на иконах и фресках. Самым известным из них является изображение невозможного треугольника, расположенного на экране перед алтарем. Он находится в церкви Святой Троицы, простроенной бенединскими монахами с 1150 по 1550 годы. На фресках обычно — это невозможная колоннада. В качестве примера можно привести изображение «Мадонна с младенцем» с миниатюры из книги Генриха II. |
|
|
В искусстве: Широко известны картины с невозможными фигурами художников, работавших, начиная со средних веков до середины прошлого века. |
|
|
В филателистке. В 1982 году по заказу правительства Швеции Оскаром Реутерсвардом были выполнены марки с изображениями невозможных фигур. Они выпускались ограниченным тиражом, сегодня являются большой редкостью и пользуются большим спросом |
|
|
Символика. Невозможные фигуры часто можно встретить в качестве изображений на часах, кружках, футболках. |
|
|
В архитектуре. Вкачестве примера невозможных фигур в архитектуре можно привести Кубические дома. Они были построены в 1984 году в Роттердаме (Нидерланды) архитектором Пиетом Бломом. Дома развернуты на угол в 45 градусов и расположены по шестиугольной сетке. Конструкция состоит из 32 кубов. Каждый кубический дом состоит из четырех этажей. Крыши домов, окрашенные в белый и серый. Этот комплекс зданий обладает одним интересным свойством. С высоты птичьего полета здания образуют конструкцию, выглядящую как невозможная фигура. |
|
|
В кинематографе. Невозможные фигуры приобретают всё большую популярность. Во многом, с моей точки зрения, это заслуга М. К. Эшера. Его работа «Относительность» послужила основой для очень многих сюжетов. Самым, пожалуй, известным является мультсериал «Симпсоны». В эпизоде» Treehouse of Horror VIII» Лиза Симпсон находит невозможный объект, выставленный на продажу, который является ничем иным как невозможным трезубцем. |
|
Для полного анализа невозможных фигур было проведено ряд исследований.
Опыт 1. Создание невозможной фигуры по фотографии, найденной в интернете [5]. Эксперимент представлен в Таблице 3.
Таблица 3
Создание невозможной фигуры из карандашей. Опыт 1
|
Примечание |
Изображение |
|
Данную картинку можно найти на просторах интернета. Карандаши, равного размера сплетены в единую конструкцию. |
|
|
Взяв за основу 4 деревянных палочки, одинакового размера, было создано сплетение их по образцу. При сближении к центру, в результате одна палочка была переломлена. На фотографии представлено максимально возможное сближение палочек в данной конструкции |
|
Опыт 2. Создание знаменитой невозможной фигуры — ленты Мёбиуса. Эксперимент представлен в Таблице 4.
Таблица 4
Создание невозможной фигуры «Лента Мёбиуса». Опыт 2
|
Примечание |
Изображение |
|
Лента Мёбиуса — самая знаменитая невозможная фигура. Суть этой фигуры, что она в пол оборота завернута. Её невозможно выпрямить и вывернуть. |
|
|
Создание данной невозможной фигуры — возможно. Сделать её может каждый, и при этом не зная её названия, многие уже воспроизводили её. Лента может быть из любого материала, который можно с одной стороны на один раз свернуть. |
|
Опыт 3. Изучив материал по данной теме [6], был составлен чертёж невозможной фигуры. Эксперимент представлен в Таблице 5.
Таблица 5
Создание невозможной фигуры «Лента Мёбиуса». Опыт 3
|
Примечание |
Изображение |
|
Чертёж невозможной фигуры, с расчетом размеров и количества элементов для создания модели из плотной бумаги формата А4. |
|
|
То что мы видим на картинке скрывает многое с обратной стороны. Искажения, тени, постановка объектов — всё это влияет на построение 3D фигуры. Но невозможные фигуры — возможно создать, нужно только время и терпение. Одна из важных частей невозможных фигур — это иллюзии. |
|
Был проведен опрос среди выпускников школы. В ходе исследования приняло участие 86 человек.
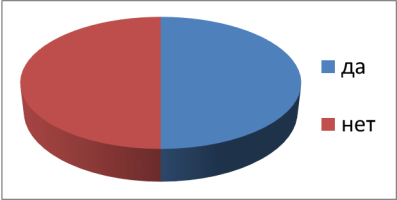
Вопрос 1. Вы что-нибудь знаете о невозможных фигурах? Результаты опроса представлены на Рисунке 3.
Многие выпускники знают о том, что такое невозможная фигура. Кто-то знает определения, а кто-то виды и применение этих фигур. Так что ученики школы имеют представление о этих фигурах.
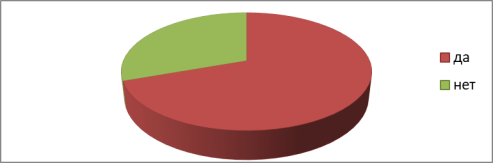
Рис. 3. Вы что-нибудь знаете о невозможных фигурах?
Вопрос 2. Где Вы встречались с невозможными фигурами? Результаты опроса представлены на Рисунке 4.
По результатам анкетирования видно, что иллюзии и невозможные фигуры в основном встречаются в интернете. Именно там многие из выпускников с ними впервые и познакомились. Так же и в реальной жизни наблюдательные подростки замечают невозможные фигуры
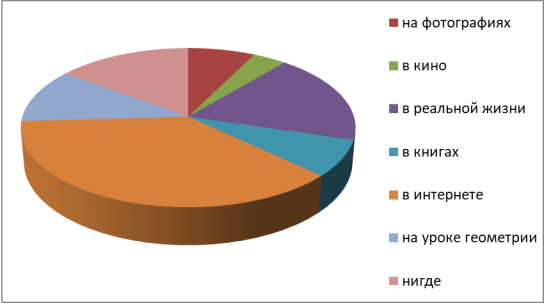
Рис. 4. Где Вы встречались с невозможными фигурами?
Вопрос 3. Пытались ли вы создать невозможную фигуру? Результаты опроса представлены на Рисунке 5.
40 % выпускников не только увлечены и знают о существовании невозможных фигур, так же они пытались сотворить некоторые из них своими руками. Это свидетельствует о том, что данная тема распространена и увлекает своей «невозможностью» людей, которые хотят проверить самим возможно ли создать фигуры или нет.
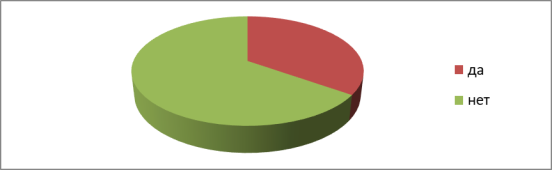
Рис. 5. Пытались ли вы создать невозможную фигуру?
Вопрос 4. Интересно ли вам рассматривать невозможные фигуры и иллюзии? Результаты опроса представлены на Рисунке 6.
75 % выпускников рассматривают невозможные фигуры и ими увлечены. Это показывает то, что данные фигуры очень редко обходят и взгляд к ним приковывается, что подтверждает еще раз Вопрос 3
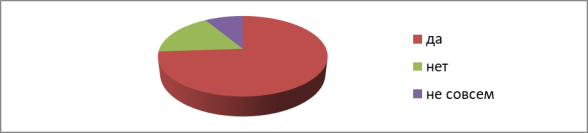
Рис. 6. Интересно ли вам рассматривать невозможные фигуры и иллюзии?
Вопрос 5. Смотрите ли вы фильмы 3D, в которых существует мир иллюзий? Результаты опроса представлены на Рисунке 7.
Во время исследования, опрошенные задавали вопросы, что имеется в виду по «иллюзиями» в 3D фильмах. Многие и не знали, что подвергаются иллюзиям, точнее не знали, что 3D эффект и называется иллюзией.
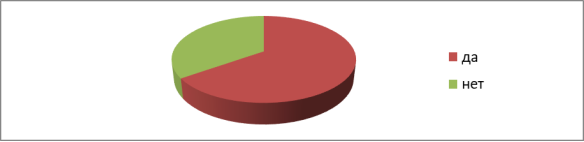
Рис. 7. Смотрите ли вы фильмы 3D, в которых существует мир иллюзий?
Вопрос 6. Считаете ли вы, что невозможные фигуры — это неотъемлемая часть современного архитектора? Результаты опроса представлены на Рисунке 8.
Практически все опрошенные считают, что невозможные фигуры являются неотъемлемой частью архитектора, — это подчёркивает то, что данная тема актуальна в наше время.
Рис. 8. Считаете ли вы, что невозможные фигуры — это неотъемлемая часть современного архитектора?
Вопрос 7. Возможно ли создать данную фигуру? Результаты опроса представлены в Таблице 6
Ответы разделились поровну. 50 % считает, что данная невозможная фигура — невозможна. Из этого следует, что они не знают о невидимых линиях, и искажениях.
Таблица 6
Возможно ли создать данную фигуру?
|
Представленное изображение невозможной фигуры |
|
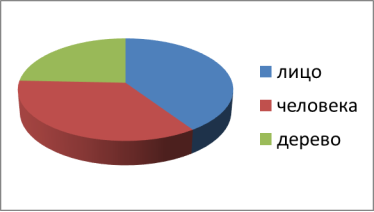
Вопрос 8. Что вы видите на фотографии? Результаты опроса представлены в Таблице 7
Данное изображение показывалось ровно 7 секунд. Видения различались. Это доказывает то, что каждый человек по-своему смотрит на иллюзии. Но треть увидела два элемента на рисунке, а половина из этих увидели все три элемента сразу.
Таблица 7
Что вы видите на фотографии?
|
Представленное изображение |
|
В результате проведенного опроса можно сделать вывод насколько восприятие человека разница. В данном опросе не учитывалась половая принадлежность. Опрошенные многие не только знают о невозможных фигурах, но и сталкивались с ними, и многим данная область вызывает интерес. Восприятие зависит от многих факторов, которые в работе не были учтены: свет, возраст, время, предпочтения опрошенных, а также внимания.
Эта тема актуальна в настоящее время. Изучение невозможных фигур имеет довольно важное значение не только с точки зрения геометрии, но и с точки зрения искусства. Они широко используются в современной рекламе, промышленной графике, плакате, оформительском искусстве и логотипах различных фирм.
Невозможные фигуры, пожалуй, самые завораживающие из всех существующих оптических иллюзий.
Литература:
- ЛитМир. Электронная Библиотека. Книга «Оптические иллюзии» Автор: Сик Эл http://www.litmir.co/bd/?b=276199http://konenko.net/imp.htm -
2. Сайт «Невозможный мир» http://im-possible.info/russian/articles/
- Статья «Математическое описание невозможных фигур» http://log-in.ru/articles/matematicheskoe-opisanie-nevozmozhnykh-figur/
- Московский государственный университет имени М. В. Ломоносова. Факультет психологии. http://www.psy.msu.ru/illusion/
- Детский сайт невозможных фигур «Затеево» http://zateevo.ru/?alias=nevozmozny_figury§ion=page
- Страна Мастеров. Развёртки невозможных фигур. http://stranamasterov.ru/node/162676
















 Кубические дома
Кубические дома
 Аватар
Аватар