В работе предлагается метод, по которому можно более простым способом решать гидродинамические задачи, связанные с неустановившейся фильтрацией упругой жидкости в пористой среде с учетом влияния начального градиента.
Ключевые слова: фильтрация, начальный градиент, давления, упругая жидкость
The paper proposes a method by which it is possible to solve hydrodynamic problems in a simpler way related to unsteady filtration of an elastic fluid in a porous medium, taking into account the influence of the initial gradient.
Keywords: filtration, initial gradient, pressures, elastic fluid
Как известно, скорость радиальной фильтрации вязкопластичной жидкости выражается в следующем виде [1]:
при 
, (1)
при 
, где 
.
Однако при решении задач, связанных с влиянием начального градиента, возникают определенные математические трудности.
В работе [2] показано, что задачи, связанные с влиянием начального градиента, можно решать более простым способом.
При этом предполагается, что фильтрация происходит по закону Дарси. Учитывая, что при наличии в пласте начального градиента созданная депрессия тратится не только на преодоление давления
на призабойной зоне, но и на преодоление начальной депрессии 
, то при 
нужно принять 
.
Как известно, основная формула теории упругого режима фильтрации имеет вид:
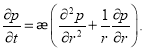(2)
В этом дифференциальном уравнении упругого режима производную от давления по времени заменяем некоторой функцией F(t), которая осредняет 
по всей возмущенной области [3]:
(3)
Значение этой функции определяется из начальных и граничных условий. Эта замена упрощает дифференциальное уравнение и облегчает его интегрирование. Тогда дифференциальное уравнение принимает вид:
(4)
При интегрировании дебит принимается постоянным. На границе возмущенной области имеем:
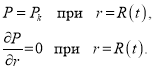(5)
Интегрируя (4), мы получаем:
(6)
Для определения F(t) используем условие (5):
или
(7)
С другой стороны,
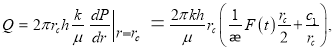
откуда получаем 
(8)
Из (7) и (8) получаем:
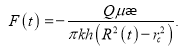(9)
Интегрируя (4) и учтя (9), получаем распределение давления:
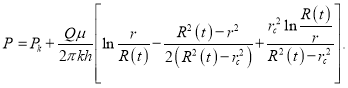(10)
Для определения координаты возмущенной области 
надо продифференцировать по t равенство (10), а результат подставить в (9).
Тогда получим для радиуса возмущенной области:
(11)
Если радиус возмущения доходит до контура питания, вместо подставляем 
Для учета влияния начального градиента при 
подставим 
и решим формулу (10) относительно Q.
Тогда получается формула в виде:
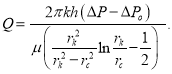(12)
Если будем пренебрегать членами 
ввиду малости относительно 
то получим выражение:
(13)
А при 
получается следующая формула:
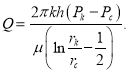(14)
Литература:
- Мирзаджанзаде А. Х., Аметов И. М., Ковалев А. Г. Физика нефтяного и газового пласта. – Москва — Ижевск: Институт компьютерных исследований. — 2005.
- Гасанов И. Р. К вопросу упрощения решений гидродинамических задач, связанных с фильтрацией в пласте углеводородов с аномальными свойствами. // Международный научный журнал -Молодой ученый № 46 (180) ноябрь 2017 г.
- К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. Подземная гидравлика. – М.: Недра, 1986.
