Анализ решения задачи о влиянии разных видов минимальных норм выпуска продукции в условиях, когда показатели эффективности производства пропорциональны расходу одного из ресурсов



Одна из работ, в которых рассматриваются вопросы влияния факторов производства на оптимальный выпуск продукции. В качестве факторов влияния выбирается минимальная относительная норма выпуска продукции первого вида ко второму виду и минимальная норма выпуска продукции второго вида. Исследуется переход решения задачи в случае пропорциональности показателей эффективности производства видов продукции расходу одного из ресурсов.

Ключевые слова: задача об использовании ресурсов, минимальная норма выпуска продукции, минимальная относительная норма выпуска продукции двух видов, относительный расход ресурса в продукции, оценка влияния фактора на доход предприятия.

В статье [1, стр. 24] была рассмотрена задача об использовании ресурсов с учётом возможного влияния минимальной относительной нормы выпуска продукции одного вида к другому и минимальной нормы производства второго вида продукции. Был проведён анализ решения задачи в условиях предпочтения выпуска второго вида продукции [2]. В этой работе рассмотрим решение задачи, когда расход одного из ресурсов пропорционален показателям эффективности выпуска продукции.

Постановка задачи. Предполагаем, что мы находимся в условиях производства, которые были определены в работе [1, стр. 24].

Рассматриваем решение пары двойственных задач, для которого расходуются полностью оба ресурса, производство удовлетворяет обеим минимальным нормам.

В статье [1, стр. 26–27] было показано, что решением прямой задачи будет план X^*=, оптимальные остатки ресурсов и отклонения от минимальных норм Y^*=.

Также в [1, стр. 27] было найдено решение двойственной задачи: u₁*=, u₂*=,u₃*= 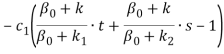, u₄*= . Решение является не единственным, зависти от двух параметров t и s. Параметры удовлетворяют условиям: t≥0, s≥0, и .

Для проведения анализа решения задачи в работах [1–6] были использованы коэффициенты k₁, k₂, β₁, β₂, k, β. В частности, они определялись в [1, стр. 25], [3, стр. 33, 35–36]. Напомним, что k = , k₁ = , а k₂ = . В работе рассмотрим два случая значений коэффициента k, когда k=k₁, и, когда k=k₂.

При k=k₁ коэффициент при t равен единице, а при s равен <1, тогда неравенство примет вид: . Если k=k₂, то коэффициент при t равен >1, а при s равен единице. Неравенство будет иметь вид: .

Условия на параметры в решении двойственной задаче станут следующими:

1) при k=k₁, так как >, то t≥0, s≥0, ;

2) при k=k₂, так как <, то t≥0, s≥0, .

Анализ решения задачи. Полагаем, что есть баланс влияния минимальных норм выпуска продукции и по использованию ресурсов. Проведём анализ решения пары двойственных задач.

Пусть k=k₁. Тогда возможны следующие варианты для условий на параметры двойственной задачи: t>0, s>0, , t=0, и s =0, .

Рассматриваем первый вариант. Решение двойственной задачи будет иметь вид:

u₁*= , u₂*= , u₃*= 0, u₄*=. Переменные удовлетворяют условиям: u₁^*>0, u₂^*>0, u₃^*=0, u₄^*<0.

Решение определяет влияние минимальной нормы n и запасов обоих ресурсов. Исходная задача переходит в задачу, в которой нет баланса по минимальной относительной норме β₀.

Перейдём к варианту, когда t=0, а . Переменные двойственной задачи равны: u₁^*=0, u₂^*= , u₃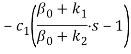^*=, u₄^*=. Переменные удовлетворяют условиям: u₁^*=0, u₂^*>0, u₃^*<0, u₄^*<0.

Решение определяется влиянием обеих минимальных норм β₀ и n и запаса ресурса R₂. Исходная задача переходит в задачу, в которой нет баланса по использованию ресурса R₁.

Теперь рассмотрим вариант, когда >1, а s =0. Переменных двойственной задачи равны: u₁^*=, u₂^*=0, u₃^*=, u₄^*=. Условия на переменные двойственной задачи: u₁^*>0, u₂^*=0, u₃^*<0, u₄^*<0.

Решение определяется влиянием обеих минимальных норм β₀ и n и запаса ресурса R₁. Исходная задача переходит в задачу, в которой нет баланса по использованию ресурса R₂.

Пусть k=k₂. В этом случае возможны также три варианта для условий на параметры двойственной задачи: t>0, s>0, , t=0, , s =0, .

Первый вариант. В общем решении двойственной задачи t>0, s>0, . Решение двойственной задачи: u₁*=, u₂*=, u₃*= , u₄*=0. Переменные удовлетворяют условиям: u₁^*>0, u₂^*>0, u₃^*<0, u₄^*=0.

Решение определяет влияние относительной минимальной нормы β₀ и запасов обоих ресурсов. Исходная задача переходит в задачу, в которой может не быть баланса по минимальной норме n.

Второй вариант: t=0, а . Переменные двойственной задачи равны: u₁^*=0,

u₂^*= , u₃^*=, u₄^*=. Значения переменных удовлетворяют условиям: u₁^*=0, u₂^*>0, u₃^*<0, u₄^*<0.

Решение определяется влиянием обеих минимальных норм β₀ и n и запаса ресурса R₂. Исходная задача переходит в задачу, в которой может не быть баланса по использованию ресурса R₁.

Рассмотрим вариант, когда >1, а s =0. Значения переменных двойственной задачи равны: u₁^*=, u₂^*=0, u₃^*=, u₄^*=. Условия на переменные двойственной задачи u₁^*>0, u₂^*=0, u₃^*<0, u₄^*<0.

Решение определяется влиянием обеих минимальных норм β₀ и n и запаса ресурса R₁. Исходная задача переходит в задачу, в которой нет баланса по использованию ресурса R₂.

Таким образом, мы рассмотрели все возможные варианты, при которых решение исходной двойственной задачи совпадает с решениями других задач.

Вводы. Когда расход одного из ресурсов по видам продукции пропорционален показателям эффективности производимой продукции, решение двойственной задачи совпадает с решением одной из трёх двойственных задач, в которых наблюдается баланс трёх из четырёх факторов производства.

Для значения k=k₁ перевод решения исходной двойственной задачи осуществляется следующим образом:

1. Если t>0, s>0, 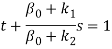, то решение исходной переводится в решение задачи, в которой нарушается баланс на производство продукции А₂ по минимальной норме.
2. Если t=0, 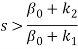, то решение исходной задачи совпадает с решением двойственной задачи, в которой нарушается баланс на использование ресурса R₁.
3. Если s =0, 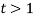, то решение исходной задачи совпадает с решением двойственной задачи, в которой нарушается баланс на использование ресурса R₂.

Для значения k=k₂ перевод решения исходной двойственной задачи осуществляется:

1. Если t>0, s>0, 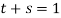, переводится в решение задачи, в которой нарушается баланс на производство продукции А₁ к продукции А₂ по минимальной относительной норме.
2. Если t=0, , совпадает с решением двойственной задачи, в которой нарушается баланс на использование ресурса R₁.
3. Если s =0, 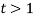, то совпадает с решением двойственной задачи, в которой нарушается баланс на использование ресурса R₂.

Литература:

1. О. В. Мамонов. Решение задачи об использовании двух ресурсов для предприятия, выпускающего два вида продукции, с учётом влияния минимальной относительной нормы производства одного вида продукции к другому и минимальной нормы выпуска продукции второго вида// Агропродовольственная экономика: научно-практический электронный журнал. Нижний Новгород: НОО «Профессиональная наука» — No3–2018. — 22–41 с.
2. А. В. Конюхова О. В., Мамонов. Анализ решения задачи о влиянии минимальной относительной нормы одного вида продукции к другому виду продукции, минимальной нормы второго вида продукции в случае баланса влияния обоих факторов, использования обоих ресурсов при приоритете выпуска второго вида продукции/ Актуальные направления развития аграрной науки в работах молодых учёных: сборник научных статей молодых ученых, посвященный 190-летию опытного дела в Сибири, 100-летию сельскохозяйственной науки в Омском Прииртышье и 85-летию образования Сибирского НИИ сельского хозяйства. ФГБНУ «Омский АНЦ». — Омск: ЛИТЕРА, 2018. — 194–198 с.
3. О. В. Мамонов. Анализ эффективного использования двух ресурсов для предприятия, выпускающего два вида продукции // Агропродовольственная экономика: научно-практический электронный журнал. Нижний Новгород: НОО «Профессиональная наука» — No12–2016. — 30–62 с.
4. О. В. Мамонов, А. В. Конюхова. Влияния технологических факторов производства в случае использования двух ресурсов/ Теория и практика современной аграрной науки: сб. национальной (всероссийской) научной конференции (г. Новосибирск, 20 февраля 2018 г.) / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 546–550.
5. О. В. Мамонов, Р. В. Луцик. Пример расчёта оценки влияния спроса на доход предприятия с двумя ресурсами: сб. трудов научно-практической конференции преподавателей, студентов, магистрантов и аспирантов Новосибирского государственного аграрного университета (г. Новосибирск, 16–17 октября 2017 г.), выпуск 2. / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 246–249.
6. О. В. Мамонов, С. В. Егорова, А. А. Пугачёва. Влияние спроса продукции двух видов и запаса ресурса на эффективность производства/ Теория и практика современной аграрной науки: сб. национальной (всероссийской) научной конференции (г. Новосибирск, 20 февраля 2018 г.) / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 542–546.