О трехчленном законе фильтрации газа сучетом влияния начального градиента иинерционных сил
Гасанов Ильяс Раван оглы, старший инженер
Научно-исследовательский проектный институт «Нефтегаз» (SOCAR) (г. Баку, Азербайджан)
Приведенные исследования показывают, что наличие начального градиента имеет место не только на нефтяных, но и на газовых месторождениях. Кроме того, начальный градиент в основном не остается неизменным в процессе разработки, а часто меняется. Существуют различные факторы, влияющие на начальный градиент 1–5. В работе делается попытка обобщения закона фильтрации при учете влияния начального градиента инерционных сил при фильтрации газа в пористой среде.
Ключевые слова: фильтрация, инерционные силы, скорость, давление, начальный градиент.
The above studies show that the presence of an initial gradient occurs not only in oil but also in gas fields. In addition, the initial gradient basically does not remain unchanged in the development process, but often changes. There are various factors affecting the initial gradient [1–5]. An attempt is made to generalize the filtration law when the effect of the initial gradient of inertial forces during the filtration of a gas in a porous medium is taken into account.
Keywords: filtration, inertial forces, speed, pressure, initial gradient.
Закон фильтрации можно написать в следующем виде:
![]() (1)
(1)
Здесь 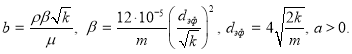
Влияние кубического слагаемого в уравнении ![]() связано с необходимостью учета неравновесных свойств фильтрационного потока и влияния инерционных сил.
связано с необходимостью учета неравновесных свойств фильтрационного потока и влияния инерционных сил.
При ![]() получается закон Дарси. При
получается закон Дарси. При ![]() получается двучленный закон Форхгеймера.
получается двучленный закон Форхгеймера.
Умножим обе части уравнения (1) на ![]() тогда уравнение принимает вид:
тогда уравнение принимает вид:
![]() . (2)
. (2)
Поставив в уравнение (2) ![]() , получим выражение:
, получим выражение:
![]() (3)
(3)
Для учета влияния начального градиента изменим пределы интегрирования. Учитывая, что для фильтрации жидкости в пористой среде с начальным градиентом депрессия тратится не только на преодоление давления в призабойной зоне ![]() но и на преодоление начального градиента призабойной зоны. Это логично, так как основное снижение давления происходит в призабойной зоне.
но и на преодоление начального градиента призабойной зоны. Это логично, так как основное снижение давления происходит в призабойной зоне.
Тогда, интегрируя левую часть от ![]() , а правую часть от
, а правую часть от ![]() получаем:
получаем:
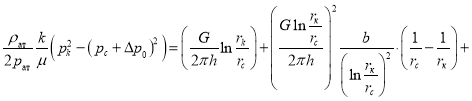
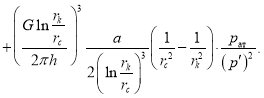 (4)
(4)
Здесь ![]() — среднее давление.
— среднее давление.
Сделав подстановки 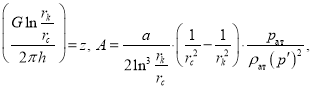
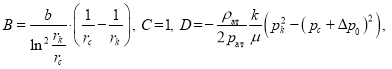
мы получаем кубическое уравнение в виде ![]() Для решения этого кубического уравнения используем подстановку
Для решения этого кубического уравнения используем подстановку ![]() Тогда данное кубическое уравнение представится в виде:
Тогда данное кубическое уравнение представится в виде:
![]()
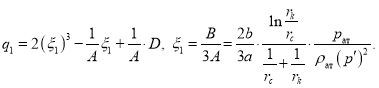 (5)
(5)
Для поставленной задачи ![]() и данное уравнение имеет всего один действительный корень, который можно найти по формуле Кардано. Решение уравнения (5) по формуле Кардано имеет вид:
и данное уравнение имеет всего один действительный корень, который можно найти по формуле Кардано. Решение уравнения (5) по формуле Кардано имеет вид:
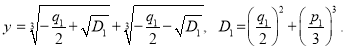 (6)
(6)
Последнее можно преобразовать в следующий вид:
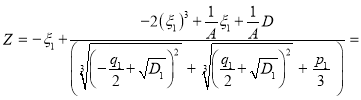
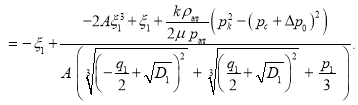 (7)
(7)
Делая подстановку 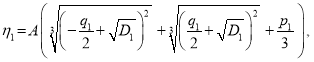 мы получаем:
мы получаем:
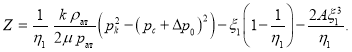 (8)
(8)
Здесь ![]() – безразмерный параметр, величина которого
– безразмерный параметр, величина которого ![]() Однако она — переменная величина. Учитывая в (8)
Однако она — переменная величина. Учитывая в (8) 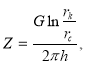 мы получаем:
мы получаем:
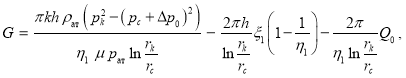
где ![]() (9)
(9)
Последнюю формулу можно написать в следующем виде:
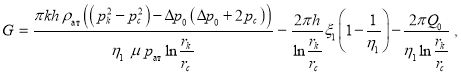
или 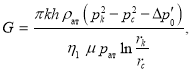 (10)
(10)
где
Учитывая, что ![]()
![]()
![]()
![]()
![]() то из формулы (10) получается формула:
то из формулы (10) получается формула:
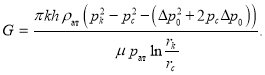
Как видно из (11), градиент давления, который направлен против движения, состоит из трех составляющих. Первая составляющая ![]() вторая —
вторая — ![]() и третья
и третья ![]()
то есть ![]()
Первая составляющая в основном связана со свойствами флюида, пористой среды и их взаимодействием на призабойной зоне. Вторая составляющая связана с коэффициентами а, b, характером изменения ![]() в процессе разработки
в процессе разработки 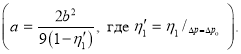 а третья составляющая учитывает влияние инерционных сил.
а третья составляющая учитывает влияние инерционных сил.
Графики изменения ![]() схематично имеют следующий вид:
схематично имеют следующий вид:
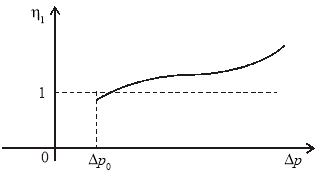
Рис. 1. График изменения параметра ![]() от депрессии
от депрессии![]()
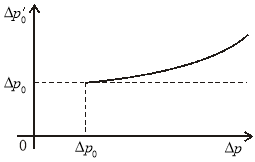
Рис. 2. График изменения ![]() от депрессии
от депрессии ![]()
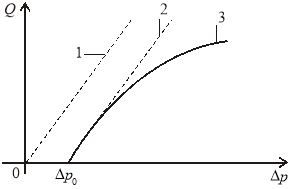
Рис. 3. График изменения Q от ![]() : 1 — по закону Дарси; 2 — влияние начального градиента; 3 — влияние инерционных сил и начального градиента.
: 1 — по закону Дарси; 2 — влияние начального градиента; 3 — влияние инерционных сил и начального градиента.
Эта задача актуальна, потому что увеличение градиента, направленное против движения, отрицательно влияет на количество извлекаемых запасов. Со временем актуальность этой задачи будет увеличиваться в связи с тем, что открываемые новые месторождения находятся на все более больших глубинах. А с увеличением глубины увеличивается и скорость, и градиент давления. Поэтому увеличиваются и сопротивления, связанные с влиянием инерционных сил.
Таким образом, в статье получена более общая формула, учитывающая начальный градиент и влияние инерционных сил. В связи с этим ее можно назвать обобщенной формулой Дюпюи.
Литература:
- А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003. — 880 с.
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. — Москва-Ижевск: Институт компьютерных исследований, 2005. — 280 с.
- А. Х. Мирзаджанзаде, А. Г. Ковалев, Ю. В. Зайцев. Особенности эксплуатации месторождений аномальных нефтей. –М.: Недра, 1972. — С.200.
- А. Х. Мирзаджанзаде, Р. С. Гурбанов. Обзор работ по гидродинамике вязкопластичных сред в бурении. — Баку: 1968. — 83 с.
- А. Т. Горбунов. Разработка аномальных месторождений. — М.: Недра, 1981. — 240 с.







