В статье рассматривается задача проектирования и оптимизации несущей системы квадрокоптера на базе рамы F450 (APM). Выполнен анализ прочности и жесткости базового проектного решения. Задача оптимизации по массе решена как задача нелинейного математического программирования в среде API приложения для SolidWorks.
Ключевые слова: квадрокоптер, несущая система, прочность, жесткость, оптимизация, нелинейное математическое программирование, многоточечные аппроксимации
Беспилотные летательные аппараты (БПЛА), в частности, квадрокоптеры получили в настоящее время широкое распространение и весьма эффективно используются в самых разных областях человеческой деятельности [1]. Это влечёт за собой существенные специфические особенности и разнообразие проектных решений для конструкций данного класса в зависимости от их целевого назначения.
Выполненный нами анализ существующих проектных решений для квадрокоптеров (Топ-10) [2] позволил нам сделать следующий вывод: наиболее рациональным выбором для реализации нашего проекта является набор компонент на базе рамы F450 (APM).
Интернет-ресурсы изобилуют руководствами по сборке квадрокоптера на базе рамы F450 и полётного контроллера ArduPilot (APM).
Наряду с существующими стандартными решениями и сборкой соответствующей натурной модели (Рис.1 а-б), рассмотрен вариант конструкции с выдвигающимся шасси (Рис. 1 в-г). При этом преследовалась цель: свести к минимуму количество и массу дополнительных деталей.
Полнофункциональная модель обладает хорошими техническими характеристиками, но наш собственный опыт эксплуатации данной модели (Рис.2) и опыт других авторов [3] побудил нас провести дополнительные исследования в части прочности и жесткости несущей системы квадрокоптера.
Рис. 1. 3D-спецификация сборки (3D via Composer) (a), испытание натурной модели (б), фотореалистическое изображение 3D модели квадрокоптера с выдвигающимся шасси (а), анимация шасси (б)
Рис. 2 Разрушение луча рамы вследствие столкновения квадрокоптера с преградой
3D модель деталей и сборки квадрокоптера была построена в среде SolidWorks в параметрической форме с визуализацией сборки (Рис.1) в среде 3D via Composer как 3D спецификация.
Анализ проектного решения в целом и напряженно-деформированное состояние основных деталей несущей системы выполнялся как средствами численного (SolidWorks Simulation), так и натурного экспериментов. Конечноэлементная модель построена с учётом возможных концентраторов напряжений со сгущением конечноэлементной сетки в областях с резким изменением геометрических параметров объекта.
Выполнено микроскопическое исследование (микроскоп ТоuрСаm UСМОЅ03100КРА) спилов луча (Рис. 3), которое показало, что полиамид, из которого изготовлен луч не включает в себя армирующих волокнистых наполнителей. Обычно используется стекловолокно в виде нитей диаметром 11 мкм. и длиной до 5–7 мм.
Таким образом, физико-механические параметры материала были взяты для данного случая в соответствии с работой [4], и для построения численной модели в среде SolidWorks Simulation для материала PA-6 (указан поставщиком в технических характеристиках детали) была выбрана модель упругопластического тела с линейным упрочнением. Модуль Юнга E=1800 МПа, предел текучести T=65 МПа.
Рис. 3. Спил луча (а), микроскопическое исследование (б).
На рис. 4 показана диаграмма растяжения синим цветом [4], а красным цветом — линейная аппроксимация зоны пластичности. Задача решалась как статическая с граничными условиями, соответствующими штатным условиям полёта.
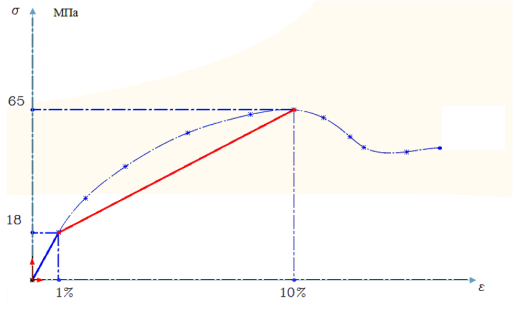
Рис. 4. Диаграмма растяжения для полиамида и её линейная аппроксимация
Натурный эксперимент проводился с использованием установки СМ-4 (Рис. 5), включающей в себя блок измерения усилий, индикатор часового типа, элементы наладки.
Рис. 5. Установка для проведения натурного эксперимента
Результаты анализа прочности и жесткости состоят в следующем: в штатных режимах полёта, т. е. при нагружении рамы лишь полезным весом (до 2 кг.) при коэффициенте динамического нагружения d=1.5 максимальные перемещения не превышают 7 мм. Максимальные эквивалентные напряжения по Мизесу не превышают предел текучести. Концентраторы напряжений имеют локальный характер (Рис.6).
Рис. 6. Результат численного эксперимента в виде карты перемещений
Максимальное расхождение результатов натурного и численного экспериментов в диапазоне внешней нагрузки на луч P= 1- 7,5 Н не превышает 8 %.
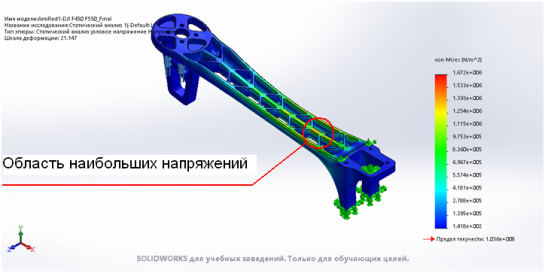
Рис. 7. Результат численного эксперимента в виде карты напряжений
Задача анализа прочности и жесткости луча с выдвигающимся шасси решалась как нелинейная контактная задача. Несмотря на наличие фиксирующей бобышки, жесткость конструкции существенно снизилась. Максимальные перемещения увеличились по сравнению с исходным вариантом на 46 %. Максимальные напряжения выросли на 20 %. Выявлено два основных концентратора напряжений: в области фиксирующей бобышки и в области контакта элемента шасси с лучом (Рис. 7).
Сформулируем задачу оптимизации конструкции луча как задачу нелинейного математического программирования:
Найти
C(X) при ограничении
,
где X =(x1, x2, x3) T — вектор управляемых параметров, C(X) — целевая функция, выражающая собой массу конструкции, 
— функциональное ограничение,
— максимальное перемещение оптимального варианта, 
— максимальное перемещение исходного варианта. В качестве x1 выбрана толщина оболочки, формируемой инструментом «Оболочка» Solidworks (Рис. 8), в качестве x2 — толщина ребра жесткости, в качестве x3 — толщина ребра жесткости в области углубления (Рис. 8).
Оптимизационная задача решалась c использованием оптимизационного API приложения к SolidWorks с поэтапной заменой исходной функции ограничений упрощенным аналитическими выражениями [5] на базе метода многоточечных аппроксимаций. Результат решения задачи: Масса луча уменьшилась на 24.4 %. Значения управляемых параметров, соответствующих оптимуму: x1=1,21 мм., x2=8.92 мм., x3=3.92 мм.
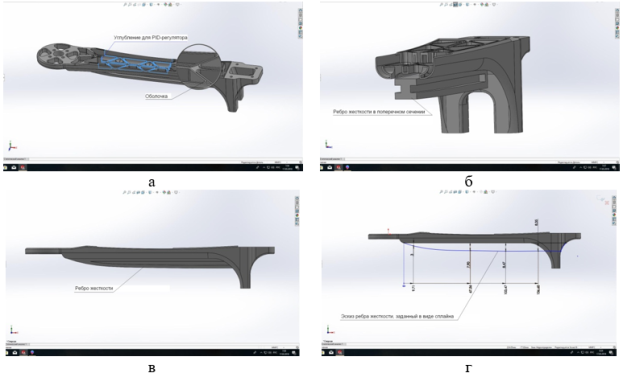
Рис. 8. 3D модель луча с оболочкой и углублением для регулятора (а), поперечное сечение луча с ребром (б), вид «справа» ребра жесткости, эскиз ребра жесткости (г)
Программная реализация задачи включает в себя построение AddIn приложений с использованием COM-технологий [6] на базе API SolidWorks, в функции которых в данном случае входит обеспечение доступа к результатам конечноэлементного анализа при каждом фиксированном наборе значений управляемых параметров (прямом расчёте оптимизационного процесса). Детали программной реализации представлены в работе [7].
Литература:
- Зулькарнаев, В.У., Камалова, В. Р. Практическое применение беспилотных летательных аппаратов в современном мире // Инновации в науке: сб. ст. по матер. LVI междунар. науч.-практ. конф. № 4(53). Часть II. — Новосибирск: СибАК, 2016. — С. 23–27. https://elibrary.ru/download/elibrary_25934551_29093911.pdf
- Дроно-мания. Интернет-журнал о дронах. Режим доступа: https://dronomania.ru/top/big-radius.html
- Ермаченков, Д.И., Фазли, Т. Г. К., Петренко, Е. О. Разработка конструкции рамы квадрокоптера для удаленного мониторинга объектов// Интернет-журнал «НАУКОВЕДЕНИЕ» Том 8, No 6(2016) http://naukovedenie.ru/PDF/45TVN616.pdf(доступ свободный). Загл. с экрана. Яз. рус., англ.
- Крыжановский, B. K. Технические свойства полимерных материалов / B. K. Крыжановский, В. Бурлов, А. Д. Паниматченко, Ю. В. Крыжановская СПб.: Профессия, 2003. –240 с.
- Чугунов, М. В. Программный модуль для решения задач оптимального проектирования в среде SolidWorks на базе API // Наука и образование: электронное научно- техническое издание. 2011. № 9, МГТУ им. Н. Э.Баумана [Электронный ресурс]. (http://technomag.edu.ru/doc/206217.html).
- Шеферд Дж. Программирование на Microsoft Visual C++.NET для профессионалов. — СПб.: Питер, 2007–928 c.
- Chugunov M. V., Schekin A. V. Practical aspects for development of Add-in SolidWorks applications on example of optimization problems// Int. Journal of Applied Sciences and Engineering Research, Vol. 4, Issue 4, 2015, pp 494–499
[1] Работа выполнена при поддержке Фонда содействия развитию малых форм предприятий в научно — технической сфере по программе УМНИК Aero.NET, договор № 11548ГУ/2017 «Разработка интегрированной модельной среды для квадрокоптера в среде SolidWorks»
