Компьютеризация средств обучения приводит к увеличению числа школьников, обращающихся в своей повседневной жизни к компьютеру, позволяющему моделировать практически любую предметную область, создавать различные учебные ситуации. Усиливающиеся влияние на подрастающее поколение различных образовательных телевизионных программ и широкое распространение всевозможных компьютерных средств существенно повлияли на отношение школьников к традиционному обучению. Профессионально написанные тексты учебников и учебных пособий, ориентированные на вдумчивую работу мысли, сейчас меньше привлекают школьников, чем красочная виртуальная реальность, возникающая на экране телевизора или мониторе компьютера, — логическая составляющая обучения математике уступает место наглядному восприятию. Возникает некое противоречие между возможностями обучаемых, владеющих общими приемами общения с информационной средой, и предлагаемыми им методами обучения в школе.
Существует множество программ, которые могут быть эффективно использованы при изучении свойств графиков функций, к ним можно отнести такие известные программы как «Mathematica», «MathCa», «Maple», «Calculator» и др. «Advance Grapher» (версия 2.2 1998–2009г.) выгодно отличается от других программ удобным интерфейсом, доступностью и простотой использования. Учителю не надо тратить много времени на объяснения, как пользоваться этой программой, а ученику на ее изучение. Она предназначена для построения и обработки графиков. При достаточно маленьком размере программа имеет невообразимо много функций и возможностей. Advanced Grapher имеет мощные средства для управления графиками. Вы можете легко создавать, удалять, дублировать графики, изменять их свойства и порядок в списке графиков.
Для управления графиками можно использовать панель инструментов «График» (рис. 1) и окно «Список графиков» (рис. 2 и 3).
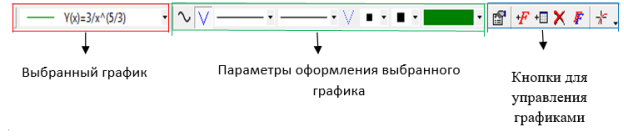
Рис. 1. Панель инструментов «График»
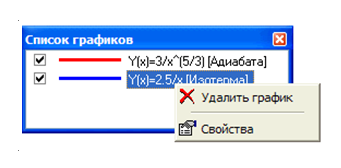
Рис. 2. Список графиков
Рис. 3. Список графиков
Advanced Grapher позволяет производить следующие действия с графиками:
– добавление нового графика. Для того, чтобы это сделать: щелкните правой кнопкой мыши в окне «Список графиков» (но не на названии какого-либо графика) и выберите команду «Добавить график» или «Добавить график таблицы» из контекстного меню (рис. 3).
– удаление существующего графика. Для того, чтобы это сделать: выделите график (с помощью комбинированного списка на панели инструментов «График» или окна «Список графиков»). Затем щелкните кнопку 
на панели инструментов «График»; или щелкните правой кнопкой мыши на названии графика в окне «Список графиков» и выберите команду «Удалить график» из контекстного меню (рис. 2).
– изменение порядка графиков. Этот порядок определяет последовательность построения графиков. Для перемещения графика на другую позицию необходимо щелкнуть левой кнопкой мыши на его названии в списке графиков и, не отпуская кнопки, перетащить название в новое положение.
– изменение свойств графика. Вы можете изменять различные свойства графика, включая параметры оформления, уравнение или таблицу, интервал построения и т. д.
Параметры оформления также можно изменить с помощью окна «Свойства графика». Это окно также показывается при добавлении или дублировании графика.
По умолчанию графики используют параметры построения, заданные в свойствах документа. Также имеется возможность настроить их для каждого конкретного графика.
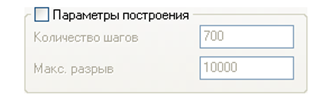
Рис. 4. Параметры построения не заданы
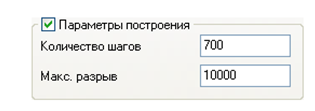
Рис. 5. Параметры построения заданы
Количество шагов определяет точность построения. Точность построения увеличивается при увеличении количества шагов. В некоторых случаях бывает полезно задать маленькое количество шагов, например, когда график строится с изображением точек (рис. 6). Количество точек в графике равно количеству шагов плюс 1.
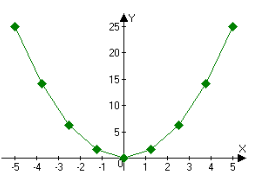
Рис. 6. График, количество шагов — 8, количество точек — 9
Совет: если Вы не задавали параметры построения для некоторых графиков, Вы можете изменить их для этих графиков (например, чтобы увеличить точность) с помощью окна «Свойства документа».
Максимальный разрыв — более сложный параметр. Это число, измеряемое в процентах от интервала. Если расстояние между двумя соседними точками больше максимального разрыва, точки не соединяются линиями. Advanced Grapher вычисляет разрыв по осям X и Y независимо. Затем он вычисляет величины РазрывX/ИнтервалX и РазрывY/ИнтервалY. Если хотя бы одно из этих значений больше максимального разрыва (например, 200 %=2), точки не соединяются линией.
Свойства графика по умолчанию
При добавлении нового графика его свойства устанавливаются в значения по умолчанию. При изменении типа графика (в окне «Свойства графика») его дополнительные свойства также устанавливаются в значения по умолчанию. Вы можете изменить свойства графика по умолчанию с помощью окна «Свойства графика по умолчанию» (рис. 7). Это окно может быть вызвано с помощью команды «Графики | Свойства графика по умолчанию» из главного меню.
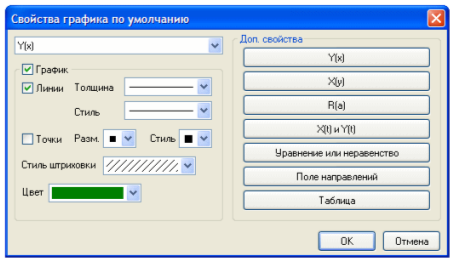
Рис. 7. Окно «Свойства графика по умолчанию»
Параметры документа определяют отображение координатной плоскости, интервалы построения и параметры построения графиков. Изменить параметры документа можно с помощью окна «Свойства документа». Его можно вызвать с помощью кнопки или команды «Графики | Свойства документа» в главном меню.
Параметры построения
Эти настройки могут быть определены с помощью страницы «Построение».
- Интервалы. Интервалы можно менять как с помощью окна «Свойства документа», так и с помощью кнопок, расположенных на панели инструментов «Стандартная» (рис. 8).
Рис. 8. Панель инструментов «Стандартная»
- Параметры построения. Опции «Количество шагов» и «Максимальный разрыв» используются как соответствующие свойства графиков по умолчанию. Опция «Выравнивание точек» может быть полезна в некоторых специальных случаях.
Пример: график функции Y(x)=x^2, количество шагов равно 7 (рис. 9 и 10).
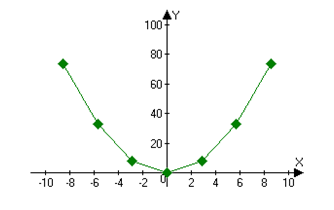
Рис. 9. Выравнивание точек включено
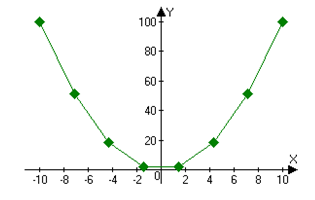
Рис. 10. Выравнивание точек выключено
– Коэффициенты. Реальные значения по осям равны видимым значениям, умноженным на коэффициенты по соответствующим осям. При определении интервалов в этом окне или в дополнительных свойствах графиков используются «видимые» значения, которые затем умножаются на коэффициент. В таблице значений при этом указываются реальные значения, которые при отображении делятся на указанный коэффициент. Например, если координата Y точки в таблице равна 6 и коэффициент по оси Y равен 2, то координата точки на экране равна 6/2 = 3.
– Коэффициенты могут быть использованы, например, при построении графиков тригонометрических функций. Если строится график функций вида Y(x), коэффициент по оси X может быть установлен в значение 3.1415927. В этом случае координаты по оси X будут измеряться в долях Пи.
– Логарифмическая шкала. Для использования логарифмической шкалы отметьте соответствующие опции («Ось X» и/или «Ось Y»). Вы также можете указать основания логарифмов.
– Легенда
Легенда может быть полезна при печати графиков и подготовке иллюстраций.
В легенде показывается описание графика. Если же оно не задано, то показывается соответствующая формула или количество точек (для графиков таблиц). Вы можете изменять описание графика с помощью окна «Свойства графика»
Пример использования программы:
Функция f(x) = 
(f(x) = abs(x^2+4*x+2)
– Запускаем программу;
– Нажимаем в пустом окне правой кнопкой мыши, и выбираем добавить график;
– Выбираем тип функции f(x), в окно ввода вписываем функцию abs(x^2+4*x+2). Выбираем по желанию цвет, толщину, и нажимаем ок;
Таким образом, эта программа является незаменимой для построения и обработки графиков, а также является прекрасным наглядным и тренировочным пособием для школьников 10–11 классов.
Из всего вышесказанного становится ясно, что программа Advance Grapher способна оказать огромную помощь учителю в объяснении материала, а школьнику — в его понимании. Однако, несмотря на все достоинства обучения на компьютере, для достижения прочных практических навыков в построении графиков необходимы тренировки с помощью карандаша и линейки. Чтобы не тратить время на построение графиков в тетради во время урока, учитель может распечатать графики, построенные с помощью компьютерной программы, и раздать их ученикам. Это является прекрасным вспомогательным пособием для выполнения домашних работ по построению графиков, так как глазами ученика будет большое количество примеров, разобранных в классе с учителем.
Основным и неоспоримым плюсом является наглядность и интересная форма подачи материала. С помощью программы легко изготовить необходимые дидактические материалы: карточки, плакаты, тесты, всевозможные формы проверочных работ. Эти задания можно поручить ученикам. Этот момент должен заинтересовать учащихся, привнести в процесс обучения момент творчества.
Несмотря на множество положительных моментов, у данной программы есть и минусы: при вычислении площадей фигур можно задавать только две функции, что ограничивает применение этой программы в школьном курсе алгебры и начала анализа. Объяснение этих моментов полностью ложится на учителя. В остальном же, программа поможет усвоению материала и привьет школьникам интерес к математике.
Литература:
- Богомолова О. Роль информационно-коммуникационных технологий на уроках математики // Математика. 2013 — № 22.
- Миндиярова Н. Использование программы «Advanced Grapher» при решении уравнений и неравенств // Математика. 2015 –№ 22.
- Холева О. Компьютерные программы для исследования функций и построения их графиков // Математика. 2016 –№ 28.
- Канкулова С. Х. Современные подходы в методике преподавания математики [электронный ресурс] — режим доступа: http//jurnal.org.ru
