Решение текстовых задач — одно из базовых умений, необходимое для успешной сдачи единого государственного экзамена. Чаще всего сложности при их решении возникают при составлении уравнения из данных задачи. Общего алгоритма составления таких уравнений нет, но эти задачи достаточно однотипные.
Всякая задача состоит из трёх частей: условие, объект и вопрос задачи. Весь процесс решения задачи можно разделить на несколько этапов: для начала нужно проанализировать условие задачи и схематично его записать, затем выбрать способ решения и осуществить его, обязательно нужно выполнить проверку решения, и, наконец, сформулировать ответ.
Рассмотрим основные типы текстовых задач.
Задачи на движение.
Если в задаче даны расстояние (
) и время (
), то скорость (
) находится по формуле: 
; если даны расстояние () и скорость (), то время находится по формуле (
).
Решая задачи «на движение», целесообразно сделать наглядный чертеж, отражающий все условия задачи.
Рассмотрим возможные виды движения двух тел.
1. Движение навстречу друг другу.
‒ Два тела движутся навстречу друг другу со скоростями 
и 
, тогда 
.
‒ Первоначальное расстояние между двумя телами, движущимися навстречу друг другу со скоростями и , равно :
.
2. Движение в противоположные стороны.
‒ Два тела движутся в противоположные стороны со скоростями и , тогда 
.
‒ Расстояние между двумя телами, движущимися в противоположные стороны со скоростями и , через время равно: 
, где 
— первоначальное расстояние между ними.
3. Движение в одном направлении.
1. Тело с большей скоростью догоняет тело с меньшей скоростью: 
2. Тело с большей скоростью «убегает» от тела с меньшей скоростью: 
Движение тел по воде.
Решая задачи на движение по воде, важно помнить, что:
‒ Скорость тела, двигающегося по (против) течению(я) реки, равна сумме (разности) собственной скорости тела и скорости течения реки.
‒ Если в условии задачи речь идет о движении плоте, то его скорость равна скорости течения реки.
Движение по кругу. Если два тела двигаются по кругу одновременно с разными скоростями
и (>), то первое тело приближается ко второму со скоростью 
, поэтому время равно: 
.
Средняя скорость — есть отношение всего пройденного пути ко всему затраченному времени. 
.
Если n-ю часть пути объект двигался со скоростью , а 
-ю со скоростью , то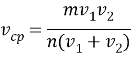 
.
Задачи на работу.
Задачи на работу характеризуются временем (), производительностью работы (p) и объемом работы (
):
A = p × t.
Задачи на растворы исплавы.
, где
P — содержание чистого вещества в сплаве или растворе в процентах, m — масса чистого вещества, M — масса сплава или раствора.
Задачи на сплавы и растворы удобно решать с помощью таблицы.
Задачи на прогрессию.
Существует два вида прогрессии: арифметическая и геометрическая.
Арифметическая прогрессия — это последовательность чисел, в которой каждое следующее число, начиная со второго, получается прибавлением к предыдущему постоянного числа: 
.
Геометрическая прогрессия — это последовательность чисел, в которой каждое следующее число, начиная со второго, получается умножением предыдущего на постоянное число: 
Задачи на сложные проценты.
, где B — будущая стоимость, A — текущая стоимость, P — процентная ставка за расчетный период (день, месяц, год,...), n — количество расчетных периодов.
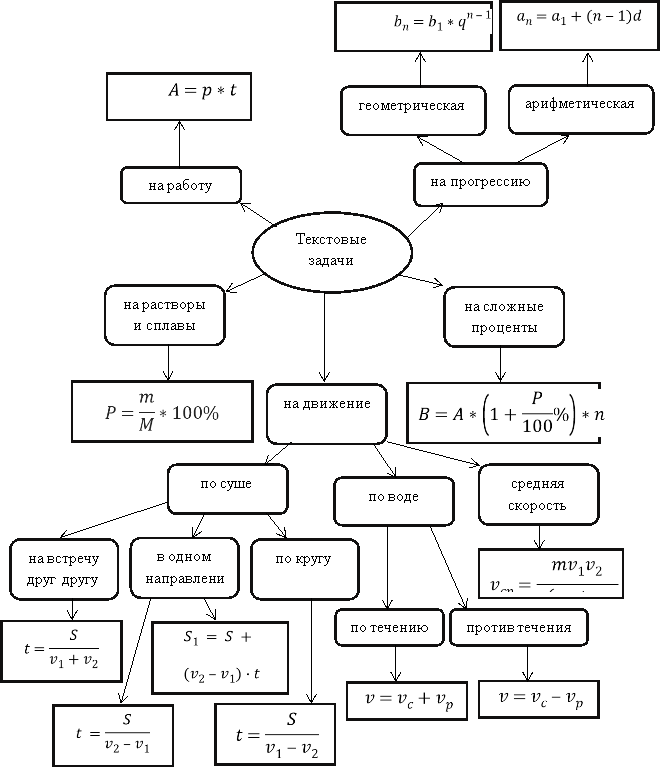
Для лучшего запоминания способов решения всех видов текстовых задач целесообразно предложить детям составить ментальные карты по данной теме.
Ментальные карты — это способ систематизации знаний с помощью схем; это технология изображения информации в особом графическом виде.
Литература:
- Майер Е. И. Возможности и преимущества использования ментальных карт в образовательном процессе / Е. И. Майер, Л. М. Бронникова // Наука и образование: новое время. 2017. № 3 (20). С. 418–421.
- Просветов Г. И. Текстовые задачи и методы их решения. — М.: Альфа-Пресс, 2010. — 48 с.
