Эффективное применение техники возможно лишь при условии ее безотказной работы с минимальными затратами на техническое обслуживание и ремонт.
Фундаментальным экономическим понятием при проектировании службы технического обслуживания на основе диагностики является функция прогрессирующих затрат. Эту функцию используют для оценки качества машины количественными методами, так как она показывает, насколько снизилась полезность или потребительская стоимость машины в результате того, что параметры состояния уже не равны исходным (паспортным) величинам и приближаются к предельно-допустимому уровню.
Функция прогрессирующих затрат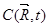 
подсчитывается как сумма двух составляющих [1].
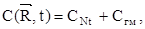(1)
где СNt – потери, связанные с уменьшением производительности машины в результате снижения мощности и надежности, руб;
Cгм – перерасход горюче-смазочных материалов в денежном выражении, руб;
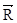– многомерный вектор технического состояния.
Для отдельного i-того параметра состояния будем иметь
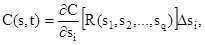(2)
Выражения (1) и (2) фактически дают стоимостное выражение негативного эффекта процессов износа и старения. Можно добавить, что благодаря выражению (2) физические размерности параметров технического состояния переводятся на язык экономики.
Снижение мощности, перерасход горюче-смазочных материалов, более частые остановки по причине поломок (снижение надежности) – все это внешние проявления непрерывно ухудшающегося технического состояния машины. Более детальный их анализ возможен при наличии соответствующих средств технического диагноза.
Не вдаваясь в частности, выведем вначале общее выражение для функции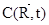 
. Для первого слагаемого СNt можно записать:
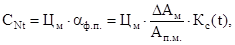
где αф.п.– коэффициент, учитывающий фактическую потребность в машинах (определенного типа или марки);
Цм – цена машины, зная которую нетрудно подсчитать потери, обременяющие ее потребителя из-за снижения мощности и простоев по техническим причинам;
Кс(t) – коэффициент сезонности. Он изменяется во времени также, как изменяется график загрузки парка машин. В момент максимальной загрузки парка он равен 1, а в общем случае варьирует в пределах от 0 до 1;
ΔАм – недовыполненный объем работы;
Ап.м. – планируемый объем работы (в фиксируемые сроки).
Недовыполненный объем работы равен разности между планируемым и фактическим объемом работ – Аф.м.
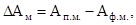
Фактический объем работы с учетом реальных показателей надежности Рм и мощности Nе.ф. определяется интегралом
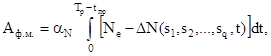
где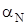 
– нормировочный коэффициент, имеющий размерность;
Ne – номинальное значение эффективной мощности, кВт;
ΔN – отклонение от фактического значения мощности от номинального;
Тр – фиксированный срок работ, ч;
tпр – время простоя равно среднему времени разового простоя парка машин (той или иной марки), умноженному на количество отказов или неисправностей машины за период Tp, т.е.
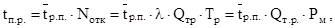(3)
где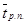 
– среднее время разового простоя, ч;
Nотк – количество отказов за время Тр;
λ – интенсивность отказов, число отказов/(кол-во машин×час);
Qтр – количество тракторов (той или иной марки);
Рм – вероятность отказов.
Известно, что параметры состояния элементов машины могут достигать предельного уровня внезапно с вероятностью Рв.о.(si), описываемой экспоненциальным законом
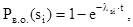(4)
и постепенно с вероятностью Рп.о.(si), определяемой дисперсионным распределением Бернштейна [2]. Это распределение правомерно, если закон износа линейный, а исходное значение и скорость распределены по нормальному закону:
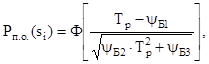(5)
где формулах (4) и (5):
λsi – интенсивность отказов, обусловленных параметром si;
Ф – символ табулированной функции нормального распределения.
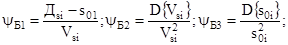
s0i – среднее исходное значение i-параметра состояния, мкм;
Vsi – средняя скорость изменения параметра, мкм/мото-час;
Дsi – предельный уровень параметра состояния, мкм;
D – дисперсия скорости износа, (мкм/мото-час)2.
Используя известные теоремы из теории вероятности, определим вероятность того, что не произойдет внезапного или постепенного отказов
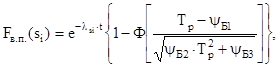
для всей машины будем иметь
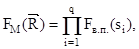(6)
Время простоев tпр за период Тр с учетом выражений (3) и (6) будет равно:
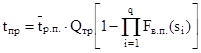
Вторая составляющая функции прогрессирующих затрат Сг.м. – перерасход горюче-смазочных материалов – определяется сразу, если вычислить интеграл
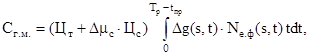
где Δg(t) – отклонение удельного расхода топлива от номинала;
Цт – цена 1 кг топлива;
Цс – цена 1 кг масла;
Δµс – разница между фактическим и нормативным значением расхода масла по отношению к расходу топлива в % (в частности если фактический угар картерного масла 4% от расхода топлива, а норма 0,5%, то Δµс = 0,035).
С учетом вышеизложенного развернутое выражение для функции прогрессирующих затрат машины имеет вид:
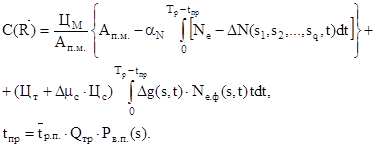
Отрицательный эффект отдельного i-того параметра состояния в денежном выражении можно оценить по следующей формуле, справедливой для малых приращений параметра,
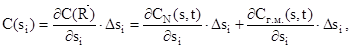(7)
Условимся называть функцию (7) парциальной функцией прогрессирующих затрат.
Наряду с абсолютным значением парциальной функции удельных прогрессирующих затрат С(si) представляет интерес также ее удельная величина:
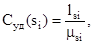
где
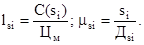
Формула для перехода от парциальной функции удельных прогрессирующих затрат к абсолютному значению имеет следующий вид:
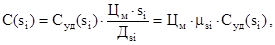
Как уже было сказано, функция прогрессирующих затрат играет очень важную роль в решении технико-экономических задач. Известна, например, методика обоснования эксплуатационных допусков, согласно которой записывают уравнение суммарных затрат, преобразуют его в целевую функцию и затем находят экстремальное значение целевой функции. Парциальное уравнение суммарных затрат имеет вид:
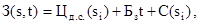
где З(s,t) – парциальная функция суммарных затрат;
Цд.с.(si) – прейскурантная цена сопряжения с i-тым параметром;
С(si) – парциальная функция прогрессирующих затрат, определяемая выражением (7);
Бзt – потери, связанные с обслуживанием или ремонтом узла (сопряжения) с i-тым параметром состояния.
Если аргумент t заменить эквивалентной переменной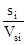 
, при изменении параметра состояния по линейному закону на непродолжительном отрезке времени, то уравнение суммарных затрат будет зависеть от величины i-того параметра состояния
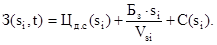(8)
Разделив все составляющие правой части уравнения (8) на текущее значение 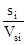, получим выражение для удельных суммарных затрат, которое называют еще и целевой функцией
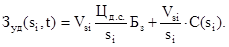(9)
Допустимый уровень Дsi равен такому значению аргумента si, при котором целевая функция достигает экстремума (в данном случае минимума). В связи с изложенным, целевую функцию (9) дифференцируют, приравнивают к нулю и находят siI = Дsi.
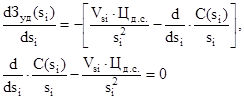
Описанная методика в первом приближении дает возможность научного обоснования эксплуатационных допусков. Она касается в основном тех элементов машины, износ которых будет происходить постепенно, причем под постепенным отказом будем понимать такое состояние элемента машины, когда параметр его состояния не меньше величины Дsi.
Литература:
1. Привалов П.В. Научно-методические принципы построения автономной системы технического сервиса технологических комплексов по производству продукции в растениеводстве / РАСХН. Сиб. отд-ние. СибИМЭ, НГАУ.ИМСХ – Новосибирск, 1997. – 92 с.
2. Бернштейн С.Н. Собрание сочинений. – М.: Наука, 1964. – 402 с.
