Необходимость непрерывного автоматического контроля изоляции в симметричных сетях 0,4 кВ обусловливается повышением надежности работы электроустановок и электроснабжения потребителей в целом. В соответствии с этим, была разработана программная реализация математических моделей автоматов Мили и Мура для точного и автоматического определения параметров изоляции.
В процессе моделирования разрабатываемого микропроцессорного устройства автоматического контроля изоляции в симметричных сетях 0,4 кВ строятся временные диаграммы работы его функциональных блоков и решаются следующие основные задачи:
– проверка правильности логической структуры разрабатываемого устройства;
– сравнение характеристик различных вариантов логических схем;
– выявление явления состязаний и риска сбоя в логических схемах.
Анализ математической модели есть эффективный инструмент, который может использоваться для предсказания поведения системы и сравнения получаемых результатов. Таким образом, моделирование позволяет логически путем прогнозировать последствия различных действий и достаточно уверенно с высокой вероятностью достоверности указывать какому из вариантов следует отдать предпочтение [1].
Данная модель представляет собой программный продукт, который разработан на универсальном языке программирования Delphi.
Для осуществления моделирования принимаются следующие начальные параметры: период импульса синхронизации элементов памяти – 1 секунда эталонного машинного времени; время моделирования 10 секунд эталонного машинного времени для управляющего микропрограммного автомата УМА Мили [2] и 11 секунд эталонного машинного времени для УМА Мура по числу состояний в графах соответствующих автоматов; метод моделирования – дискретный с фиксированным шагом; размер шага моделирования – фиксированный, автоматический; режим автоматический; для имитирования входных сигналов используются блоки единичного перепада сигнала в заданное время; для отображения результатов моделирования используются диаграммы; моделирование осуществляется при выполнении и невыполнении логического условия Х1 (наличие напряжения в электрической сети).
Внешний вид окна программы УМА Мили устройства микропроцессорного устройства автоматического контроля изоляции в сетях 0,4 кВ представлен на рис.1, который иллюстрирует процесс его моделирования [2].
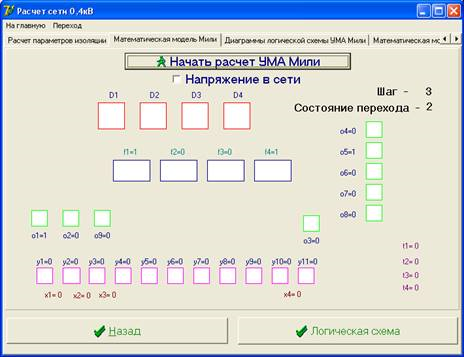
Рис.1. – Окно программы УМА Мили устройства микропроцессорного устройства автоматического контроля изоляции в сетях 0,4 кВ
При выполнении логического условия Х1 (наличие напряжения в электрической сети) в результате моделирования получены следующие диаграммы (рис.2): диаграмма выходных сигналов (микрокоманд); диаграмма входных сигналов (логических условий); диаграмма состояний элементов памяти (D-триггеров).
При невыполнении логического условия Х1 в результате моделирования получены следующие диаграммы (рис.3): диаграмма выходных сигналов (микрокоманд); диаграмма входных сигналов (логических условий); диаграмма состояний элементов памяти (D-триггеров).
Логическая схема и граф модели УМА Мура данного устройства представлены на рис. 4, иллюстрирует процесс моделирования управляющего микропрограммного автомата Мура. При выполнении логического условия Х1 в результате моделирования получены следующие диаграммы (рис. 5): диаграмма выходных сигналов (микрокоманд); диаграмма входных сигналов (логических условий); диаграмма состояний элементов памяти (D-триггеров).
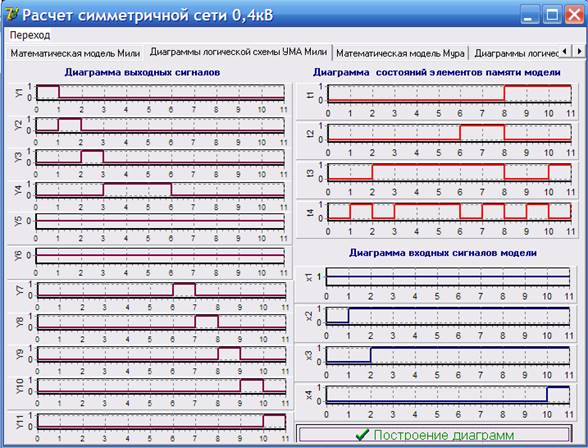
Рис. 2. Диаграммы модели УМА Мили при выполнении условия Х1.
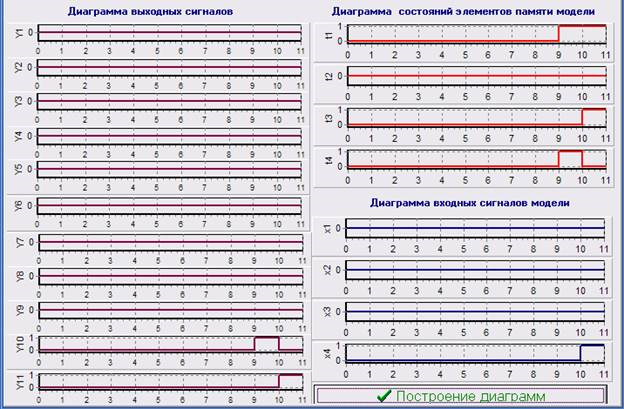
Рис. 3 – Диаграммы модели УМА Мили при невыполнении условия Х1.
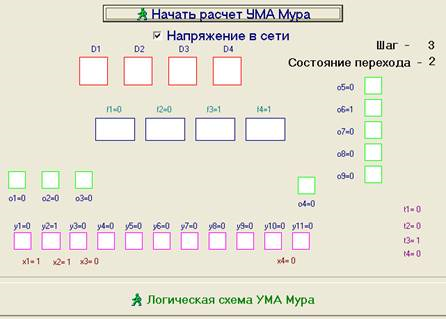
Рис. 4. Окно программы УМА Мура устройства микропроцессорного устройства автоматического контроля изоляции в сетях 0,4 кВ
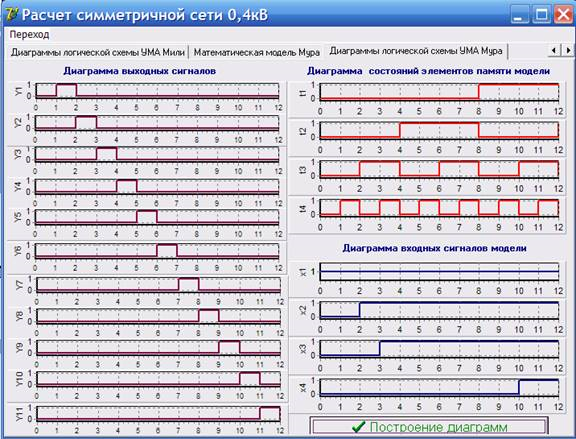
Рис. 5. Диаграмма входных сигналов модели УМА Мура при выполнении условия Х1.
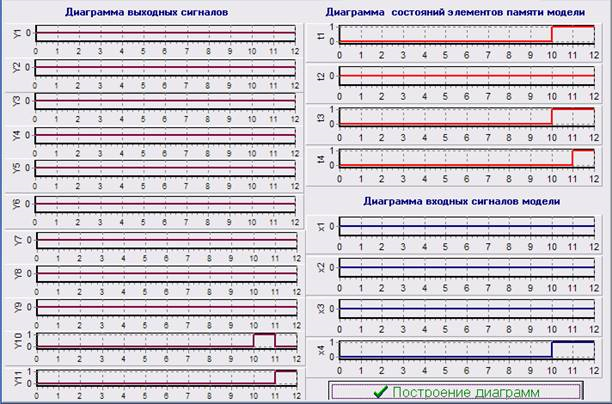
Рис. 6. Диаграммы модели УМА Мура при невыполнении условия Х1.
При невыполнении логического условия Х1 в результате моделирования получены следующие диаграммы (рис. 6): диаграмма выходных сигналов (микрокоманд); диаграмма входных сигналов (логических условий); диаграмма состояний элементов памяти (D-триггеров).
На диаграммах выходных сигналов моделей управляющего микропрограммного автомата Мили и Мура показан ступенчатый переход от одной микрокоманды к последующей согласно графу автомата при выполнении логических условий. При невыполнении условия Х1 (отсутствие напряжения в электрической сети) происходит переход к микрокоманде Y10 (отсчет заданного интервала измерения), что показывает безошибочную работу разработанных моделей управляющих микропрограммных автоматов Мили и Мура данного устройства. Диаграммы состояний элементов памяти моделей управляющего микропрограммного автомата Мили и Мура соответствуют кодам состояний данных автоматов.
Из диаграмм выходных сигналов моделей управляющего микропрограммного автомата Мили и Мура следует, что выходные сигналы автомата Мура вырабатывается с задержкой на один такт, чем в автомате Мили. Это объясняется различием данных моделей, заключающемся в том, что в автомате Мили выходной сигнал возникает одновременно с вызывающим его входным сигналом, а в автомате Мура - с задержкой на один такт. Таким образом, выходной сигнал оказывается зависящим от входного сигнала в предыдущий момент времени. Учитывая вышеперечисленные отличия в качестве основной математической модели микропроцессорного устройства автоматического контроля изоляции в сетях 0,4 кВ, принимается за основу автомат Мили.
Таким образом, была разработана программная реализация моделей автоматов Мили и Мура для симметричных сетей 0,4 кВ, позволяющие автоматически определять и контролировать параметры изоляции на городских предприятиях, повышая тем самым электробезопасность и надежность их работы.
Литература:
1. Е.С. Аскаров. О научной работе. Руководство для аспирантов, соискателей и магистров. Учебное пособие. Алматы 2002.
2. Статья в международной научной конференции «Разработка управляющего микропрограммного автомата Мили устройства автоматического контроля состоянии изоляции в симметричных сетях напряжением 0,4 кВ» г. Омск 2009.

