Трафик — объём информации, передаваемой через компьютерную сеть за определённый период времени.
Трафик является главной составляющей любой системы связи. Для того, чтобы обеспечить качество обслуживания входящих потоков трафика, нужны некоторые методы его анализа, которые смогли бы учесть все требования пользователей и сетевых систем, а также позволяли бы получать основные характеристики сети.
Информация или пакеты группируются в «пачки» в одних промежутках времени и практически отсутствуют — в других промежутках. Случайный процесс поступления заявок (пакетов) в систему характеризуется законом распределения, устанавливающим связь между значениями случайной величины и вероятностями появления указанных значений. В большинстве случаев, поток характеризуется функцией распределения временных интервалов между соседними заявками.
Любой пакетный трафик является продуктом компьютерной обработки, выполняемой процессором при решении задач приложений. Решение любой задачи состоит из трех последовательных этапов: получение исходных данных, процесс обработки и процесс выдачи результатов. Это и обуславливает его пачечный характер [1].
Для получения или снятия трафика нужно воспользоваться программой WireShark. Wireshark — это известный инструмент для захвата и анализа сетевого трафика. Wireshark работает с большинством протоколов, имеет понятный и доступный графический интерфейс и мощную систему фильтров. Работает в таких ОС как Linux, Solaris, FreeBSD, NetBSD, OpenBSD, Mac OS X и Windows, — т. е. кроссплатформенный. Система нужна не только для того, чтобы проводить исследования сетевых приложений и протоколов, а также, находить проблемы в работе сети, и, что особенно важно, выяснять причины этих проблем.
Захват трафика производился с обычного фильма в течение нескольких секунд. После этого захват был остановлен. На основе полученных данных создается файл, в котором отображено время между приходом пакетов (примерное количество пакетов 20000). Этот файл будет обрабатываться уже посредством другой программы — системой АМС (автоматическая моделирующая система), разработанная Лихтциндером Б. Я.
Система АМС нужна для анализа характеристик потоков заявок, представляющих пакеты или кадры МСС. Интерфейс основного окна программы состоит из трех блоков: панель с потоками, график и панель настройки отображение графика.
На первом этапе пользователь загружает в систему файл, содержащий время прихода пакетов во время функционирования МСС, то есть файл, полученный ранее с помощью программы WireShark. Первый элемент равен 0000, последний — 10000.
Рассмотрим некоторые характеристики трафика при различных коэффициентах загрузки 0,1 и 0,6, полученные посредством анализа системой АМС.
1) Входной поток
Составляющими входного потока являются — коэффициент загрузки, = — число заявок, поступающее в течение интервала обслуживания одной заявки. При этом, в течение указанного интервала может поступить больше одной заявки или не поступить ни одной. Полученная величина считается мгновенным коэффициентом загрузки, а ее математическое ожидание является коэффициентом загрузки. Здесь же, — средняя интенсивность поступления заявок в потоке, а — время обработки одной заявки. Величина, показывающая, сколько приборов обрабатывает в данный момент поток заявок, это — количество приборов, равная, в данный момент, единице. Входные потоки с разными коэффициентами загрузки одинаковы.
2) A(t) — число заявок на интервале.
Отображает числа заявок, поступающих в систему в течение последовательных интервалов времени , равных среднему времени обработки одной заявки.
В связи с тем, что поток заявок обладает существенной неравномерностью, в нем наблюдаются периоды с разной активностью. Указанные периоды чередуются между собой во времени с различными вероятностями появления, причем, в течение каждого периода присутствует лишь один вид потока. Отсутствию заявок соответствует период нулевой активности.
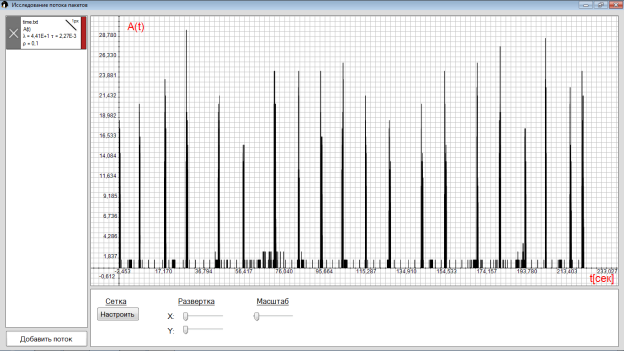
Рис. 1. Число заявок на интервале с =0.1
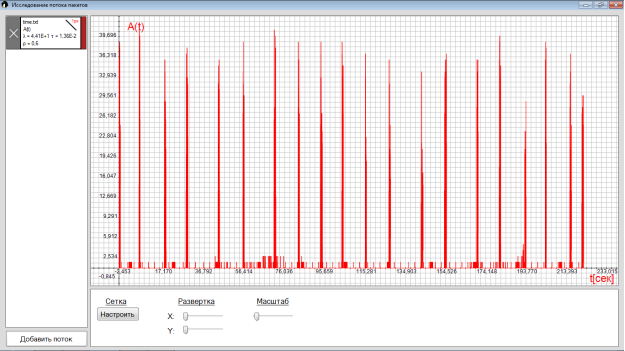
Рис. 2. Число заявок на интервале с =0.6
3) mA() — математическое ожидание или среднее значение числа заявок.
На графике видна зависимость среднего числа заявок, поступающих в течение интервалов времени , от коэффициента загрузки . График имеет линейную зависимость для любых видов потоков.
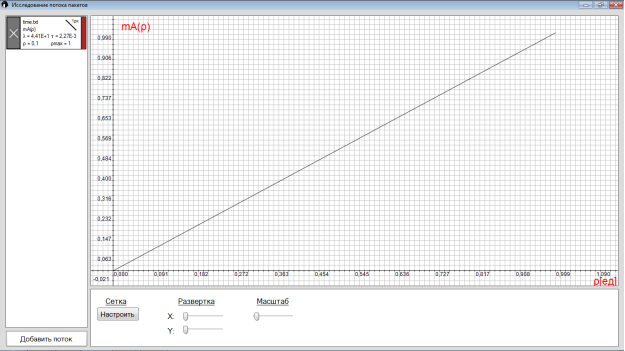
Рис. 3. Математическое ожидание
4) dispA() — дисперсия времени обслуживания заявок или разброс значений относительно математического ожидания
Дисперсия и корреляционные свойства числа заявок, поступающих за интервал обработки, оказывают основное влияние на средний размер очереди. На графике видна зависимость дисперсии числа заявок, поступающих в течение интервалов времени , от коэффициента загрузки .
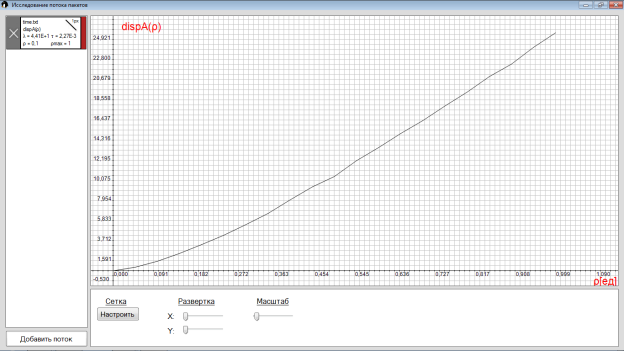
Рис. 4. Дисперсия
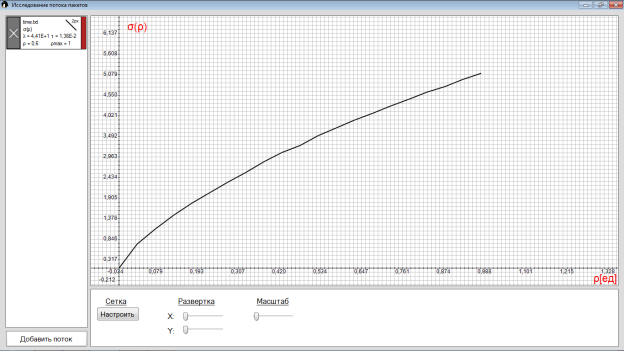
Рис. 5. Зависимость среднеквадратичного отклонения размеров очереди от коэффициента загрузки 
5) q(t) — размер очереди i-ом интервале или числа заявок в очереди, на интервалах , соответствующих моментам времени t и коэффициенту загрузки .
Средние размеры очередей зависят, по отдельности, не от распределения интервалов между заявками и распределения интервалов обработки, а от их совокупности. А именно, от распределения числа заявок, поступающих в течение интервалов обработки каждой из заявок. Данная величина характеризует изменение коэффициента загрузки системы.
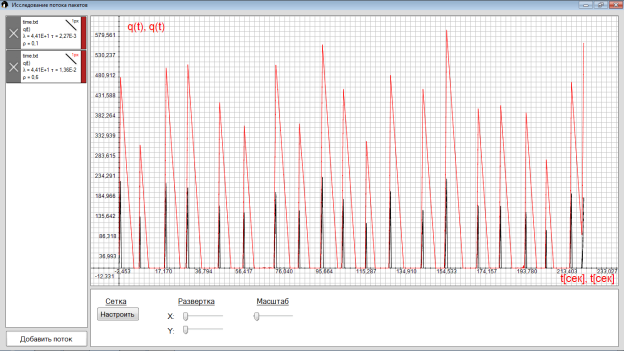
Рис. 6. Число заявок в очереди
6) mq() — математическое ожидание размера очереди или зависимость среднего числа заявок, в очереди, от коэффициента загрузки .
График отображает зависимость среднего числа заявок, в очереди, от коэффициента загрузки , максимальное значение которого равно единице.
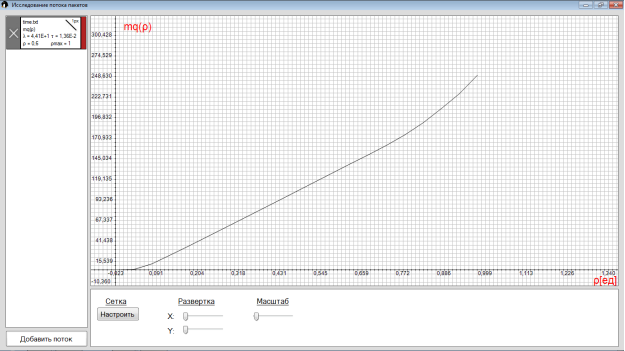
Рис. 7. Математическое ожидание размера очереди
7) P(i) — вероятности чисел заявок или вероятность того, что интервал заполнен заявками; вероятности прихода i-заявок, в течение интервалов времени , соответствующих коэффициенту загрузки .
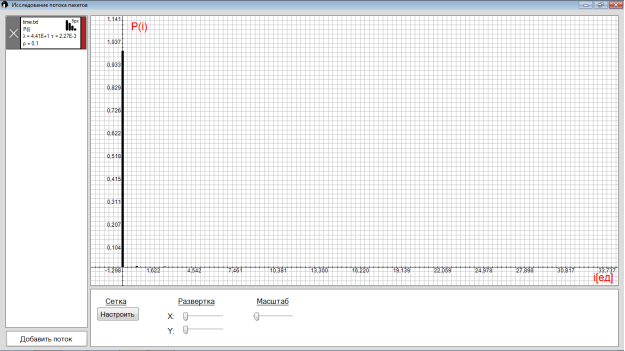
Рис. 8. Вероятности чисел заявок с =0.1
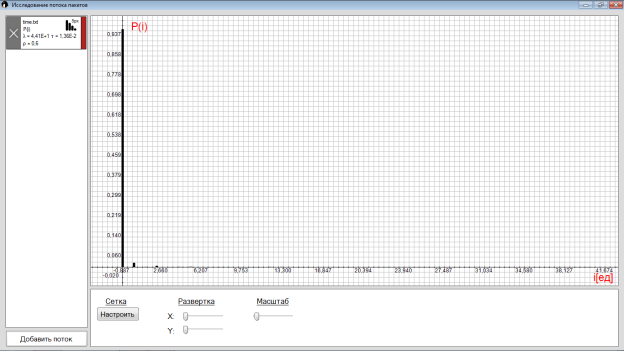
Рис. 9. Вероятности чисел заявок с =0.6
8) P0(i) — условная вероятность без нулей или вероятности отсутствия пакетов на интервалах ; условные вероятности прихода i- заявок, в течение интервалов времени , соответствующих коэффициенту загрузки. Для пачечного трафика распределение отличается от пуассоновского и имеет нулевую составляющую [2]. Поэтому, в системе предусмотрено два режима измерения: с учетом и без учета нулевой составляющей.
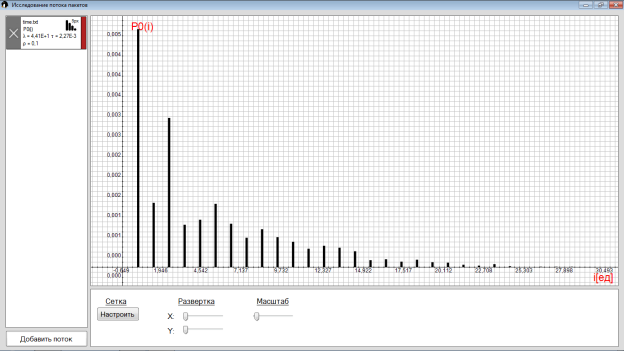
Рис. 10. Вероятность отсутствия пакетов с =0.1
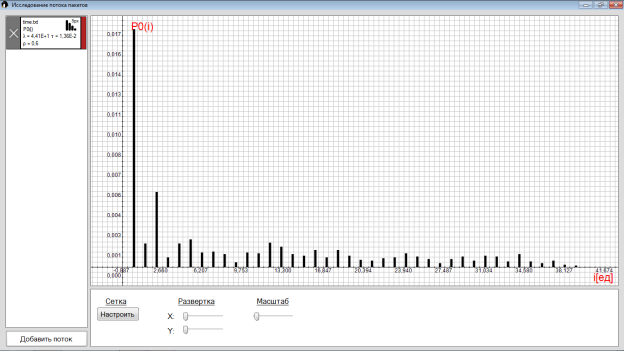
Рис. 11. Вероятность отсутствия пакетов с =0.6
9) 9) 
– аппроксимация зависимости среднего значения дисперсии размеров очереди 
от коэффициента загрузки .
После нажатия кнопки «ОК» система АМС показывает значения коэффициентов 
и 
. В данном случае: 
, 
, =0,05
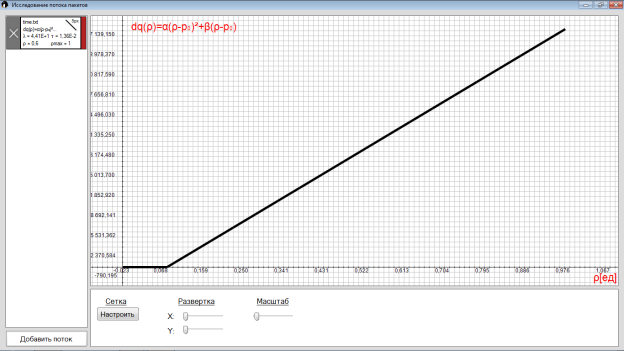Рис. 12. Аппроксимация зависимости среднего значения дисперсии размеров очереди
Таким образом, с помощью автоматической моделирующей системы был проведен некоторый анализ видео трафика. После этого можно установить, что потоки не всегда являются Пуассоновскими. Для этого и были рассмотрены графики зависимостей некоторых величин.
Литература:
- Лихтциндер Б. Я. Анализ трафика мультисервисных сетей. Учебное пособие. – Самара.: ПГУТИ 2013. — 164 с.
- Лихтциндер Б. Я. Интервальный метод анализа трафика мультисервисных сетей доступа. Монография. – ПГУТИ, Самара, 2015. – 121 с.
