Математическое ожидание и дисперсия распределения на соседних временных интервалах должны не очень сильно отличаться, поэтому их оценки могут быть получены в результате интерполяции по значениям, хранящимся в специально для этого созданной таблице моментов (имеются в виду 1 и 2 моменты случайной величины). В ходе экспериментов было установлено, что метод квадратичной интерполяции позволяет получить наиболее точные значения оценок математического ожидания и дисперсии. Для отслеживания цикличности сообщений информационной безопасности(ИБ) используется таблица моментов.
Для того чтобы определить пороговые значения для количества сообщений ИБ необходимо знать оценки математического ожидания и дисперсии количества сообщений ИБ на заданном интервале времени. Оценки математического ожидания и дисперсии количества сообщений ИБ могут быть получены несколькими способами. Очевидным решением является сохранение исторических данных для каждого возможного интервала времени [1]. Преимуществом такого подхода является то, выявление отклонений производится на основании сравнения с достоверными историческими данными, и таким образом повышается точность определения аномалий. Недостатками такого подхода является то, что, во-первых, необходимо хранить большое количество данных (значения оценок математического ожидания и дисперсии) для каждого из временных интервалов, во-вторых, данное решение является не масштабируемым с точки зрения архитектуры, поскольку изменение интервала времени потребует изменения структуры базы данных и программного кода, реализующего подобный функционал.
В статье на основании эмпирических данных было показано, что значения оценок математического ожидания и дисперсии количества сообщений ИБ на соседних временных интервалах не сильно отличаются друг от друга, а изменение этих значений происходит достаточно плавно [2]. В подобной ситуации возможно сохранять лишь ключевые значения оценок математического ожидания и дисперсии количества сообщений ИБ, например, значения оценок для каждого часа, и получать остальные значения оценок математическими методами. Фактически задача заключается в том, чтобы по известным точкам построить функцию, на которую могли бы с высокой точностью попадать значения оценок математического ожидания и дисперсии количества сообщений ИБ. Такая задача называется аппроксимацией кривой и решается методами экстраполяции или интерполяции.
Таким образом, в статье оценки математического ожидания и дисперсии количества сообщений ИБ на соседних временных интервалах будут получены методом интерполяции по ключевым значениям, хранящимся в специально созданной для этого таблице моментов. К сложностям данного такого подхода относится то, что выбранный способ интерполяции должен обеспечивать достаточную точность, чтобы давать результаты, совпадающие в пределах погрешности с реальными историческими данными. К преимуществам такого подхода являются оптимизация количества сохраняемых данных и хорошая масштабируемость.
Существует несколько способов интерполяции. На практике чаще всего применяют интерполяцию многочленами. Это связано с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса) [3]. Были исследованы следующие возможные варианты интерполяции многочленами (табл. 1):
− линейная;
− квадратичная;
− кубическая.
Таблица 1
Сравнение способов интерполяции
|
Наименование |
Способ интерполяции |
Размах вариации (сообщ.) |
Среднее отклонение (сообщ.) |
Коэффициент осцилляции |
Линейный коэффициент вариации |
|
Оценка мат. ожидания кол-ва сообщ. ИБ |
Линейная |
9.2 |
1.5 |
0.083 |
0.013 |
|
Квадратичная |
5.3 |
0.7 |
0.048 |
0.006 |
|
|
Кубическая |
5.2 |
0.7 |
0.047 |
0.006 |
|
|
Оценка дисперсии кол-ва сообщ. ИБ |
Линейная |
1.1 |
0.2 |
0.088 |
0.013 |
|
Квадратичная |
0.7 |
0.1 |
0.052 |
0.007 |
|
|
Кубическая |
0.6 |
0.1 |
0.047 |
0.006 |
Эмпирические данные показывают, что линейная интерполяция часто приводит к результатам, которые значительно отклоняются от достоверных исторических значений. При этом как квадратичная, так и кубическая интерполяция позволяют получить достаточно точные оценки, совпадающие с историческими данными в пределах погрешности. Поэтому в рамках данной работы для расчета оценок математического ожидания и дисперсии количества сообщений ИБ используется квадратичная интерполяция, поскольку она позволяет достичь необходимой точности и при этом является более простой в использовании по сравнению с кубической интерполяцией.
Далее выводятся формулы для расчета оценок математического ожидания и дисперсии количества сообщений ИБ по значениям, содержащимся в таблице моментов. Пусть xt- это количество сообщений, полученное на t-ом интервале времени, который соответствует циклу с, часу h(1≤h≤H) и минуте m(1≤m≤M), где Н=24 — количество часов в дне, М=60 — количество минут в часе.
Таким образом, на первом шаге происходит получение оценок математического ожидания ![]() и дисперсии
и дисперсии ![]() нормального распределения на t-ом интервале времени в результате квадратичной интерполяции значений математического ожидания и дисперсии, хранящихся в таблице моментов {(Eh,Dh):h=1,…..,H}.
нормального распределения на t-ом интервале времени в результате квадратичной интерполяции значений математического ожидания и дисперсии, хранящихся в таблице моментов {(Eh,Dh):h=1,…..,H}.
Пусть арифметическое среднее М=60 математических ожиданий, полученных в результате интерполяции в рамках одного часа, равно соответствующему значению Eh из таблицы моментов. Аналогично арифметическое среднее М=60 дисперсий, полученных в 63 результате интерполяции в рамках одного часа, равно соответствующему значению Dh из таблицы моментов.
Тогда, если взять три последовательных часа (-1,0],(0,1],(1,2], то можно определить коэффициенты квадратичной интерполяции (А,В,С):
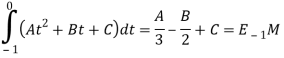
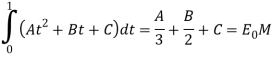
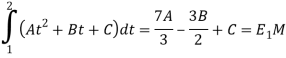 (1)
(1)
Решение данной системы уравнений относительно А, В,С дает:
A=M(E-1-2E0+E1)/2
B=M(E0-E-1)
C=M(2E-1+5E0-E1)/6
Пусть ![]() две последовательные минуты, тогда значение оценки математического ожидания, полученное в результате процедуры интерполяции, соответствующей минуте
две последовательные минуты, тогда значение оценки математического ожидания, полученное в результате процедуры интерполяции, соответствующей минуте ![]() часа
часа ![]() равно:
равно:
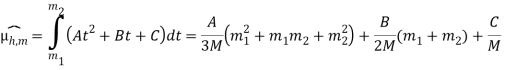 (2)
(2)
В более общем виде выражение выглядит следующим образом:
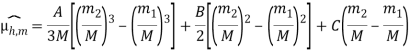 (3)
(3)
Таким образом, выведено выражение для расчета оценки ![]() из сохраненных значений математических ожиданий в таблице моментов.
из сохраненных значений математических ожиданий в таблице моментов.
Аналогичным образом для дисперсии:
A′=M(D-1-2D0+D1)/2
B′=M(D0-D-1)
C′=M(2D-1+5D0-D1)/6
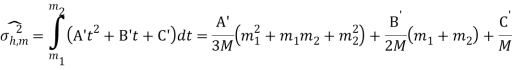 (4)
(4)
В более общем виде выражение выглядит следующим образом:
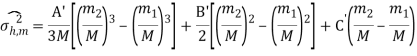 (5)
(5)
Интерполяция коэффициентов (А, В, С) и (А', В', С'), использующихся для расчета оценок математического ожидания и дисперсии, происходит раз в час. Интерполяция сглаживает как значения внутри часа, так и между часами, поскольку коэффициенты зависят от хранящихся в таблице моментов оценок для данного часа, а также двух смежных с ним часов.
Литература:
- Thottan M. Proactive anomaly detection using distributed agents / M. Thottan, C. Ji // IEEE Network. — 1998. P. 21–27.
- Ковалев Д. О. Оценка количества сообщений ИБ в автоматизированных системах как метод выявления сетевых атак / Д. О. Ковалев, Н. Г. Милославская // Безопасность информационных технологий. — 2011. – №1. С. 44–50.
- Интерполяция [Электронный ресурс]: Веб-сайт / Wikipedia. 2009. — Режим доступа к Веб-сайту: http://wikipedia.ru [ссылка]







