В работе рассмотрено представление алгоритма в матрично-предикатном виде двумя способами: модульном и функционально-предикативном. Рассмотрено параллельное взаимодействие компонентов путём применения операции композиции.
Алгоритм — заранее заданное, понятное и точное предписание совершить определенную последовательность действий для получения решения задачи за конечное число шагов.
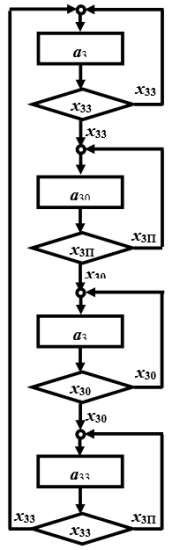
Рис. 1. Граф-схема алгоритма работы ворот ГТС
Наиболее употребимыми способами задания алгоритмов [1–4] являются следующие:
– словесный;
– графический;
– псевдокод;
– программный.
В технических специальностях чаще всего применяются графические способы: блок-схемы, граф-схемы и т.п. Рассмотрим более подробно различные способы задания алгоритма функционирования двухстворчатых ворот ГТС.
Работа двухстворчатых ворот определяется следующими командами:
a3 – Створки верхних ворот стоят
a30 - Створки ворот открываются
a33 - Створки ворот закрываются
и положением створок:
x30 – Верхние ворота открыты
x33 - Верхние ворота закрыты
x2П - Верхние ворота в промежуточном положении
время работы ворот: открытия – t30, закрытия – t33
Запишем работу двухстворчатых ворот граф-схемой алгоритма (рис. 1). Любая ГСА является графом с двумя типами вершин: вершинами команд (в дальнейшем будем их называть блоками действия — Д) и вершинами положений (в дальнейшем будем их называть предикативными или логическими блоками — Л). Запишем ГСА в виде двудольного графа G3 (Рис.2).
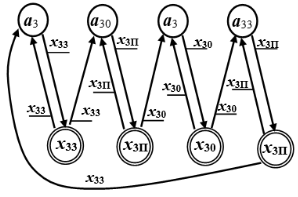
Рис. 2. ГСА в виде двудольного графа G3
При таком начертании ГСА и графа G3, описывающих функционирование двухстворчатых ворот, имеет место некоторая неопределённость: из состояния, характеризуемого парой a3 — x33, переход в следующее состояние a30 — x3П осуществляется по сигналу x33, то есть по тому же сигналу, который характеризует предыдущее состояние. Это происходит потому, что сигналом на открытие ворот служит сигнал от другого компонента.
Для исправления указанного недостатка достаточно «доопределить» некоторые переходы между состояниями, например, в вышерассмотренном переходе сигнал x33 заменить на сигнал x33–30, означающий переход к выполнению команды открытия ворот — a30.
В результате получим доопределённые ГСА (рис. 3) и графа G3* (рис. 4).
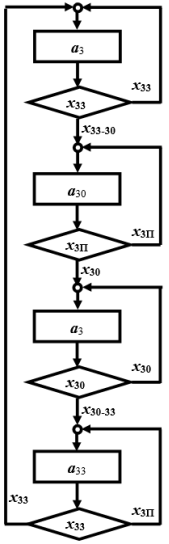
Рис. 3. Доопределённая граф-схема алгоритма работы ворот ГТС
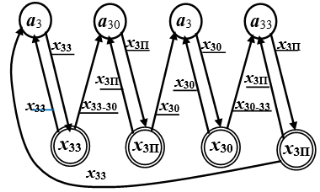
Рис. 4. Доопределённый двудольный граф G3*
Связанную пару, состоящую из функционального — Д и предикативного — Л блоков, будем называть функционально-предикативным модулем — М. Таких модулей в рассматриваемом алгоритме четыре (рис. 5), а изображение алгоритма в модульном исполнении (рис. 6).
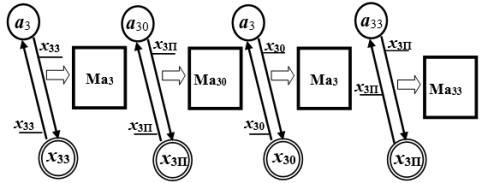
Рис. 5. Модули доопределённой ГСА

Рис. 6. Изображение алгоритма в модульном исполнении
Использование матрично-предикатного способа [5–8] представления модулей алгоритма позволяет задать алгоритм в виде матрицы. На рисунке (рис. 7) показана запись алгоритма функционирование двухстворчатых ворот в матрично-предикатном виде в модульном варианте, а на рисунке (рис. 8) показана запись алгоритма функционирования двухстворчатых ворот в матрично-предикатном виде в модульном варианте
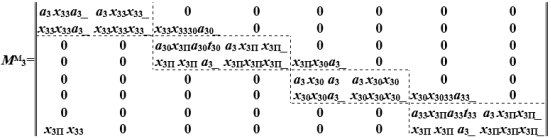
Рис. 7. Матрица алгоритма функционирование двухстворчатых ворот в матрично-предикатном виде в модульном варианте
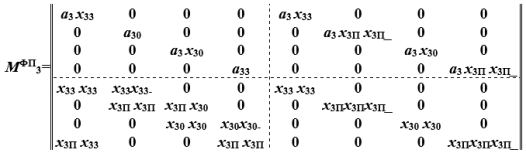
Рис. 8. Матрица алгоритма функционирование двухстворчатых ворот в матрично-предикатном виде в функционально-предикативном варианте
Задание алгоритма в виде матрицы имеет ряд преимуществ, так как позволяет использовать аппарат теории матриц. Рассмотрим параллельное взаимодействие двух алгоритмов: алгоритм функционирования двухстворчатых ворот (рис. 7) и: алгоритм изменения уровня воды в камере (рис. 9).

Рис. 9. Матрица алгоритма изменения уровня воды в камере
Каждый из компонентов, алгоритмы функционирования которых приведены на рисунках (рис. 7 и рис.9), характеризуются множеством признаков:
первый — {a3, a30, a33, x30, x33,x3П};
второй — {u, uВ, uН, xВ, xН,xП}.
Из элементов этих множеств составляются истинные значения предикатов, из которых строятся матрицы алгоритмов компонентов. Рассмотрим произвольный элемент декартова произведения двух компонентов.
aixii ai_
bjyjj bj_
Будем считать, если попарное существование признаков двух компонентов ai и bj; xii и yjj; ai и yjj; xii и xii; допустимо, то рассматриваемый элемент декартова произведения двух компонентов существует. Наличие такой пары указывает на существование процесса в этой точке. Чтобы определить все допустимые элементы декартова произведения двух компонентов, необходимо определить, допустимость попарного существования троек компонентов. Для этой цели вводится бинарное отношение на множестве признаков компонентов. Бинарное отношение может быть задано в виде таблицы, где допустимость признаков обозначается — 1, а недопустимость их — 0.
Рассмотрим параллельное взаимодействие (композицию) двух алгоритмов MMU и MM3, для чего определим их декартово произведение.

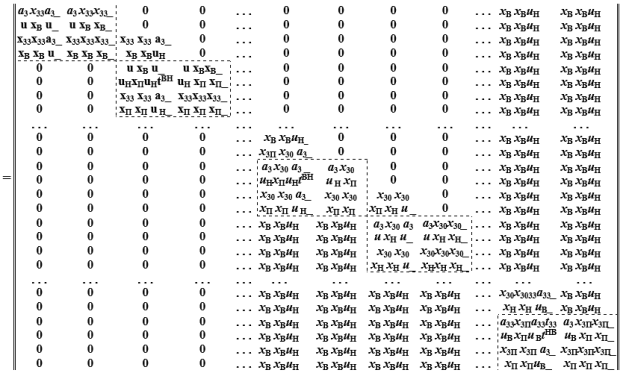
Операция композиции определяется с помощью бинарного отношения ω, которое задаётся таблицей.
|
ω= |
a3 |
a30 |
a33 |
x30 |
x33 |
x3П |
|
|
u |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
uВ |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
uН |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
xВ |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
xН |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
xП |
0 |
0 |
0 |
0 |
0 |
0 |
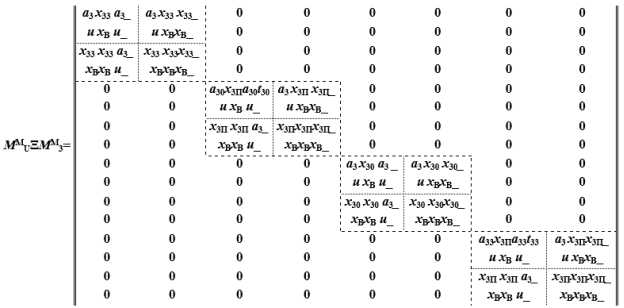
Операция композиции состоит в том, что из результирующей матрицы декартова произведения ММU с помощью бинарного отношения ω удаляем те пары, которые не описывают параллельное взаимодействие компонентов. В итоге получим матрицу [MMUΞMM3], определяющую композицию алгоритмов функционирования компонентов: верхних двухстворчатых ворот и изменения уровня воды в камере.
Литература:
- Крупский В. Н., Плиско В. Е. Теория алгоритмов. — М.: Academia, 2009. — 208 с.
- Кормен Т. Х., Лейзерсон Ч. И. и др. Алгоритмы. Построение и анализ. / Пер. с англ. — М.: Вильямс, 2015–1328 с.
- Миллер Р., Боксер Л. Последовательные и параллельные алгоритмы / Пер. с англ. — М.: Бином. Лаборатория знаний, 2000–408с.
- Паронджанов В. Д. Учись писать, читать и понимать алгоритмы. Алгоритмы для правильного мышления. Основы алгоритмизации.– М.: ДМК Пресс, 2012. — 520 с.
- Поляков В. С. Построение формального описания технологического процесса в матрично-предикатной форме / В. С. Поляков, С. В. Поляков, П. В. Федченков // Известия ВолгГТУ. Серия «Прогрессивные технологии в машиностроении». Вып. 9: межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2013. — № 7 (110). — C. 105–108.
- Поляков В. С. Использование нагруженных матриц инцидентора (операторов) для моделирования сложных систем / В. С. Поляков, С. В. Поляков // Контроль. Диагностика. — 2013. — № 3. — C. 57–62.
- Поляков В. С. Представление алгоритма в матрично-предикатном виде / Поля ков В. С., Поляков С.Вл. // European research. — 2016. — № 2. — С. 29–35.
- Поляков В. С. Матричный способ представления алгоритма / Поляков В. С. // Молодой ученый. — 2016. — № 6 (ч. 2). — С. 159–163.







