Эта статья написана, прежде всего, для студентов, готовящихся стать учителями начальных классов. В ней описана система заданий для младших школьников, которая позволяет повысить мотивацию, активировать творческие способности учащихся, в игровой форме освоить новый материал.
Точность и чёткость формулировок при определении понятия любого объекта является главным условием в понимании самого объекта и его свойств [1]. Грамотно построенные вопросы учителя, побуждение к логическим действиям естественно подводят учащихся к восприятию учебной темы.
В предыдущей нашей работе [2] на примере учебной темы «формирование разрядов в позиционных системах счисления» был описан способ подачи нового материала, основанный на создании образа, легко запоминаемого учащимися; движении фигуры, её трансформации в другую фигуру, в которой видны все составляющие элементы, естественно воспринимаемые учащимися.
В данной работе на примере учебных тем «сложение чисел» и «вычитание чисел» будет описан подход авторов к проведению занятий по этим темам, предложена новая система заданий.
Сложение однозначных чисел.
Число – это количественная характеристика объекта.
Однозначное число – это число, в написании которого используется только один знак (символ) без повторения.
При написании чисел используются знаки (символы), которые обычно называют Цифрами. Обычно мы используем десять цифр (т.н. «арабские цифры»):
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Рассмотрим однозначные числа. Очевидно, что их всего десять, и они совпадают с арабскими цифрами. Для любого однозначного числа совокупность (множество) однозначных чисел разбивается на две части (подмножества). Первое подмножество – однозначные числа, сложение с которыми выбранного однозначного числа в сумме дает однозначное число.
Пример.
Выберем число 6. Для этого числа множество однозначных чисел разбивается на два подмножества: первое – числа от 0 до 3; второе – числа от 4 до 9.
И так происходит с любым числом в этом множестве. Попробуйте сами и убедитесь!
Число 10.
Этому числу уделим большее внимание. Во-первых, в написании этого числа используется два различных знака: первый – 1; второй – 0. Что они обозначают? 1 – количество десятков. 0 – количество единиц следующего десятка [2].
Посмотрим, как оно записывается. Представьте себе вертикальный столбик, в котором находится десять разноцветных предметов. На какую цифру этот разноцветный столбик похож? Количество предметов в нём – десять, сколько десятков мы имеем? Ответ - один. Цифра, обозначающая это количество – 1.
Здесь проявилась гениальная догадка человека: поставить эту цифру рядом с только что написанным числом слева, потому что оно старше написанного. А что нам мешает сжать этот столбик до палочки, похожей на цифру 1. Поставим её рядом с написанным числом СЛЕВА и запомним, что это – один десяток, а на место, где раньше были написанные цифры, поставим цифру 0. Она будет обозначать количество единиц следующего десятка, но их нет, пусто, а пустое множество мы обозначаем цифрой 0.
Так обозначилось число ДЕСЯТЬ – двумя различными цифрами. И процесс набора повторился. Так образовалась запись числа десять. Эта мысль дала возможность поместного написания цифр, обозначающих общее количество взятых предметов, а место для написания нового значения данного числа назвали разрядом числа.
Сколько цифр можно уместить на этом месте, разряде? Только десять. Потому что других цифр мы не используем. Это оказалось и не нужным. Описанный процесс можно сделать наглядным. Цифры 1, 2 и т.д. появляются с количеством единиц в следующем десятке. Это происходит до набора полного десятка. Сколько полных десятков мы набрали? Ответ – 2 десятка. В разряде десятков мы должны написать цифру 2. Цифру 0 надо поставить в разряде единиц этого числа. Этот набор производится до момента появления 10-го десятка, который по аналогии переходит в следующий разряд – одной сотни. Разряды десятков и единиц – обнуляются. Обнуление единиц младшего разряда является окончанием выполнения задания.
Записывать эти примеры хорошо было бы «в столбик», т.к. вся последующая работа учащегося происходит сложением и вычитанием в столбик.
Для учащихся 1-х классов нужно давать задания такого типа: составить примеры на сложение и вычитание так, чтобы результатом было однозначное число. Примеры на вычитание дать после практической работы.
Такую практическую работу, к сожалению, ученики не выполняют ни в школе, ни в подготовительных группах. А зря! Такие задания приучают ребёнка к самостоятельности, уверенности в правильности своих действий, они перестают бояться аналогичных заданий, данных им учителем.
Приведем пример такой практической работы.
Практическая работа для учеников 1 класса.
На листе бумаги нарисовали карандашом любую замкнутую фигуру любого размера. Обозначили внутреннюю часть фигуры числом 5. Вырезали её. Внутри фигуры нарисовали ещё одну любую замкнутую фигуру. Обозначили её цифрой 3. Теперь по контуру вырезали фигуру, обозначенную цифрой 3. Удалим её. Каким числом обозначить то, что осталось? Подсознание подсказывает ответ – числом 2.
Вопрос: Что произошло с размером первоначальной фигуры?
Ответ: Он уменьшился.
Вопрос: Назовите математически действие удаления.
Ответ: Вычитание.
Вопрос: Назовите результат действия удаления.
Ответ: Остаток.
Вернёмся к примеру.
Первое число назвали уменьшаемым. Оно уменьшилось. Второе число назвали вычитаемым. Третье число назвали остатком или разностью между уменьшаемым и вычитаемым.
Продолжение. Попробуем восстановить фигуру.
Вопрос: Что нужно сделать с вырезанной фигурой?
Ответ: Объединить вырезанную фигуру с оставшейся.
Вопрос: Какое математическое действие напоминает Вам эта операция?
Ответ: Сложение.
Вывод: Действие вычитания проверяется действием сложения.
Первый тип примеров (без перехода через десяток).
Пример на сложение:

Пример на вычитание:

Первый тип примеров на сложение и вычитание без перехода через десяток в каждом разряде учащиеся усвоили и выполнили.
В первом типе примеров учащиеся понимают, что можно вычислить сумму не только записав выражение строчкой. Можно в столбик. Оказывается, можно выбрать самостоятельно такие слагаемые, которые в сумме с данным числом дадут в результате число, меньшее десятка. Таких вариантов может быть несколько. Можно выбрать любой. Результатом будет число меньше десяти. Смелее вперёд. Второй тип примеров более сложен.
После усвоения заданий 1-го типа, можно перейти ко 2-му типу заданий. Для этого нужно обязательно ещё раз повторить тему «образование десятка» и разобраться в теме сложение чисел с переходом через десяток.
Второй тип примеров (с переходом через десяток).
Напишем любое число, например 4. Прибавим к нему любое число из “второго подмножества”. Например, 7. Число 7 мы представим в виде суммы «удобных» слагаемых (6+1). Далее применим правило прибавления к числу суммы двух слагаемых. К числу 4 прибавляем число 6. Получаем число 10, один десяток. Этот один десяток мы переводим в число 1 и записываем эту 1 в разряде десятков, рядом со вторым слагаемым:
4 + 7 = 4 + (6 + 1) = 10 + 1 = 11.
Второй способ:
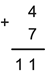
Разделим вертикальными рядами разряды чисел.
В каждом одноимённом разряде напишем сумму двух слагаемых с переходом через десяток. Первое слагаемое – произвольное число. Второе слагаемое выберем из второго множества, чтобы сумма с первым слагаемым в данном разряде была двузначным числом. Найдем их сумму. Рядом с числом 4 напишем ещё произвольную цифру, например, 3 и прибавим к ней любое число из второго подмножества так, чтобы сумма этих чисел была двузначным числом. И так в каждом разряде.
Это уже творческий процесс. Он зависит только от действий самого ученика.
Пример на сложение:
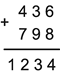
Первое число – произвольное, его составляет ученик. Второе слагаемое ученик подбирает, затем подсчитывает сумму.
Первое слагаемое составляю произвольно. По одной цифре в одном разряде. Сколько цифр написать? Сколько хочу. Хоть до конца строчки. Не забыть поставить плюс слева. Перехожу ко второму слагаемому. Второе слагаемое нужно записать под первым: единицы под единицами, десятки под десятками, сотни под сотнями и т. д. Подбирая числа так, чтобы они в сумме с верхним числом давали двузначное число в данном разряде. Но находить сумму двух слагаемых буду после написания всего примера. Начинаю сложение. Не забывать единичку присчитывать в каждом старшем разряде. Дохожу до крайней левой цифры. Число десятков (один) записываю левее.
Ученик сам создал пример и сам подсчитал его результат. Он научился самостоятельно составлять пример на сложение и вычитание без помощи других.
Третий тип примеров (смешанный).
Назовем его смешанный тип.
А как это?
Первое слагаемое записываю произвольно. Второе слагаемое записываю под первым. При сложении, надо учитывать, в каком разряде надо переносить единицу в старший разряд, а в каком нет. Этим примером отрабатывается внимание ученика.
Пример на сложение.
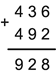
Первое число – произвольное, его составляет ученик. Второе слагаемое ученик подбирает, затем подсчитывает сумму.
Мы видим, что в первом и третьем разрядах сумма цифр одноименных разрядов не превышает десяти, а во втором разряде – больше десяти.
Четвёртый тип примеров (круглое число).
В четвёртом типе примеров при сложении и вычитании создаём круглое число.
Пример на сложение:
Первое слагаемое произвольное число. Второе слагаемое записываем под первым, столбиком, подбираем цифры так, чтобы сумма цифр одноименных разрядов оканчивалась на ноль, т.е. десятком.
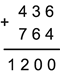
Первое число – произвольное, его составляет ученик. Второе слагаемое ученик подбирает, затем подсчитывает сумму.
Пример на вычитание:
Первое число – уменьшаемое, создается учащимся произвольно. Старший разряд – число отличное от нуля, остальные разряды – нули. Под ним записывается вычитаемое – произвольно. Далее выполняется вычитание. Выбираем случай, когда цифра старшего разряда уменьшаемого меньше самого вычитаемого.
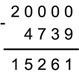
Самостоятельная работа.
Первый тип примеров (без перехода через десяток).
Пример на сложение .

Пример на вычитание.

Второй тип примеров (с переходом через десяток в каждом разряде).
Пример на сложение .

Пример на вычитание.

Третий тип примеров (смешанный).
Пример на сложение .

Пример на вычитание.

Четвертый тип примеров (с круглым числом).
Пример на сложение .

Пример на вычитание.

Выводы
Системы предложенных в работе заданий в настоящее время нет ни в одном учебнике по математике для начальной школы. Тем не менее, ее использование позволяет повысить мотивацию, активировать творческие способности учащихся, в игровой форме освоить новый материал. Считаем целесообразным дополнить такой системой новые учебники по математике для начальной школы. Необходимо использовать данный материал в контрольных работах студентов-педагогов, планирующих работать в начальной школе. Это поможет повысить профессионализм будущих преподавателей.
Литература
1. Лазарев М.А., Воробьева Н.А., Прончев Г.Б. Теоретико-дидактический подход к формированию понятия // Журнал Профессиональное образование / Приложение “Новые педагогические исследования. 2007. № 1. С. 75 – 77.
2. Лазарев М.А., Воробьева Н.А., Прончев Г.Б. Формирование понятия разряда в позиционной системе счисления / в кн.: Исследования в профессиональном образовании. Сборник статей аспирантов и докторантов. Выпуск 1, М.: НОУ “ИСОМ”, 2007, С. 37 – 40.

