Правила тяговых расчетов для поездной работы тягового подвижного состава были введены в 1980 г. и с тех пор практически не пересматривались. На тот момент наиболее точным методом расчета являлся графо-аналитическим. Но данный метод имеет свои недостатки, одно из которых это допущение что поезд с локомотивом представляется в виде материальной точки. В настоящее время в АО РЖД сложилась тенденция к увеличению массы и длины состава, это позволяет значительно эффективнее использовать тяговый подвижной состав и локомотивные бригады.
Но вождение длинносоставных поездов требует внесения коррективов в правила тяговых расчетов, так как поезд может двигаться сразу по нескольким участкам с различными профилем и уклонами. А допущения, что поезд материальная точка, в этом случае введет только к увеличению погрешности при расчетах.
Определение значений V и S при моделировании движения поезда осуществляется путем численного интегрирования уравнения движения. При этом на каждом шаге интегрирования производится вычисление правой части уравнения по значениям координат скорости и пути, полученным на предыдущем шаге. Отличие предлагаемой методики тягового расчета от традиционных состоит в специальной подготовке данных о профиле пути, суть которой заключается в следующем.
- Исходный профиль пути первоначально обрабатывается согласно ПТР. На этом этапе производится приведение уклонов и кривых к эквивалентным уклонам по схеме, изображенной на рис. 1, а. Исходными данными служат: массив уклонов в тысячных и их длин в м, массив радиусов кривых в м и их длин (или углов поворота кривых в градусах).
- Исследуемый участок пути разбивается на n равных отрезков l (рис. 1,б). Длина элемента l выбирается в зависимости от длины поезда и требуемой точности тягового расчета. Величина уклона на границах каждого отрезка l определяется путем спрямления элементов профиля, находящихся в данный момент под всем составом поезда по ранее выведенной формуле.
Таким образом, преобразовав исходный профиль пути с учетом длины поезда по описанной методике, его можно использовать для уточненных тяговых расчетов, в том числе по имеющимся программам для ЭВМ.
Перед входом поезда на уклон i2 его полное сопротивление движению
![]() (1)
(1)
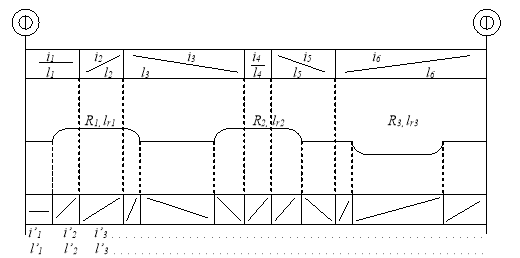
а)

б)
Рис. 1. Спрямление профиля пути с учетом конечной длины поезда
Находясь, в начале участка пути с уклоном i2,полное сопротивление движению поезда равно
![]() (2)
(2)
что равнозначно вступлению поезда на эквивалентный уклон ![]() определяемый из выражением
определяемый из выражением
![]() (3)
(3)
Из сопоставлений выражений (2) и (3) находим:
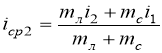 . (4)
. (4)
Продолжив движение по уклону i2, полное сопротивление движению поезда определяется следующим образом
![]() (5)
(5)
или
![]() (6)
(6)
Из сопоставления выражений (5) и (6) получим:
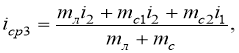
где mл, mс — масса локомотива и состава;
mс1 — масса части состава, располагающегося на первом элементе профиля пути;
mс2 — тоже на втором элементе профиля.
При расположении поезда на трёх элементах профиля
![]()
или
![]()
Откуда среднее значение уклона, действующего на поезд в этом положении определяется как
![]() , (7)
, (7)
где mл, mс — масса локомотива и состава;
mс1 — масса части состава, располагающегося на первом элементе профиля пути;
mс2 — тоже на втором элементе профиля,
mс3 — тоже на третьем элементе профиля.
Этот способ построения эквивалентного (с учётом длины и массы поезда) профиля пути целесообразно применять в том случае, когда задан подробный попикетный профиль и план линии. Применение попикетного профиля хотя и увеличивает объём расчётов, но компенсирует существенным повышением точности построения интегральной кривой скорости движения. В этом случае выражение для определения среднего уклона, действующего на поезд, принимает вид
![]() ,
,
где mл, mс — масса локомотива и состава;
mс,n — масса части состава, располагающегося на n-ом элементе профи ля пути.
Значения уклонов в каждый момент времени могут быть приведены не только для центра тяжести поезда, но и для любой его точки. Так если «привязываем» мгновенные и расчётные значения уклонов для головы поезда, то можно затем производить непосредственное сравнения расчётных значений скорости с показаниями скоростемера на локомотиве или с данными скоростемерной ленты.
Расчёты таким способом производим следующим образом. Заранее определяем среднестастическую длину и массу поезда. Если на участке имеются кривые, то их заменяют приведёнными уклонами в каждом элементе попикетного профиля, на котором они расположены, по выражению
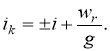
Учитывая значительную трудоемкость расчетов, целесообразно использовать средства вычислительной техники.
Так как для решения тяговой задачи будет использоваться среда программирования Microsoft Excel, поэтому рассмотрим процедуру преобразования профиля пути с учетом конечной длины поезда именно этот табличный процессор. Составим блок-схему программы расчета (рис. 3). При разработке блок-схемы предполагалось, что поезд может находить не более, чем на 3-х элементах.
При составлении блок-схемы приняты следующие обозначения:
S — координата головы поезда,
S0 — координата начала элемента профиля пути, на котором находится голова поезда.
S-1 — координата начала последующего элемента профиля пути,
Блок-схема работает следующим образом. В блоке 2 производится ввод исходных данных о профиле пути. В блоке 3 производится определение местоположения поезда и находится элемент профиля пути, на котором находится его голова. Если поезд полностью убирается на этом элементе, то управление передается блоку 6, в противном случае — блоку 4. В этих блоках вычисляется удельное дополнительное сопротивление движению поезда от уклона, которое численно равно самому уклону: в блоке 6 для всего поезда
wi = i0,
а в блоке 4 для той его части, которая находится на найденном уклоне
wi = i0 (S — S0)/ lп.
После расчетов блок 4 передает управление блоку сравнения 5, назначение которого определить этап тягового расчета: начало или нет. Если найденный профиль пути является первым в базе данных, то считается, что поезд полностью помещается на нем не зависимо от его длины и управление передается блоку 6. В противном случае происходит переход к блоку 10.
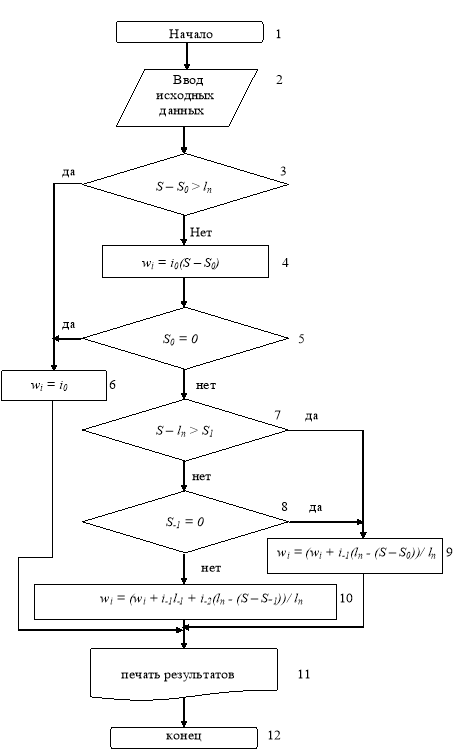
Рис. 3. Блок-схема программы преобразования профиля пути с учетом конечной длины поезда: lп — длина поезда, l0, l-1 — длины соответствующих элементов профиля пути, i0, i-1 — уклоны соответствующих элементов профиля пути, wi — удельное дополнительное сопротивление движению поезда от уклона с учетом конечной длины поезда в точке пути с координатой S
wi = (wi + i-1(lп — (S — S0))/ lп.
В этом блоке проверяется, помещается ли хвост поезда полностью на предыдущем элементе профиля пути или нет. Если да, то далее расчеты производятся блоком 9, если нет — блоком 8. В блоке 9 рассчитывается удельное дополнительное сопротивление движению от хвостовой части поезда по формуле:
В блоке 8 проверяется является ли исследуемый элемент профиля пути первым в базе данных. Если да, то считается что вся оставшаяся часть поезда располагается на этом элементе и расчет сопротивления движению продолжается в блоке 9. Если же нет, то в блоке 10 рассчитывается сопротивление движению из условия, что хвостовая часть поезда располагается на двух элементах профиля пути. Расчет производится по формуле
wi = (wi + i-1l-1 + i-2(lп — (S — S-1))/ lп.
После выполнения всех расчетов результаты вычисления блоком 11 выводятся на печать и(или) передаются в программу для дальнейшего использования в тяговом расчете.
На основе рассмотренного алгоритма в среде EXEL была разработана программа.
Проведенные расчеты свидетельствуют о работоспособности разработанного алгоритма и программы. Поэтому описанный выше алгоритм был может быть использован в программе тягового расчета.
Литература:
- Осипов С. И. и др., Основы тяги поездов, М., УМК МПС России, 2000 г.
- Правила тяговых расчетов для поездной работы. Утв. МПС в 1985г., М., Транспорт, 1985г.
- Тяговые расчеты. Справочник под ред. П. Т. Гребенюка, М., Транспорт, 1992г.
- Петров Ю. П. Оптимальное управление движением транспортных средств. — Л.: Энергия, Ленингр. отд-ие, 1969. — 96 с
- Петров Ю. П. Оптимальное управление электрическим приводом с учетом ограничений по нагреву. — Л.: Энергия, Ленингр. отд-ие, 1971. — 144 с
- Осипов С. И., Миронов К. А., Ревич В. И. Основы локомотивной тяги. М., «Транспорт», 1979–440 с.;
- Осипов С. И. Рациональные режимы вождения поездов и испытания локомотивов. М., «Транспорт», 1984–280 с.;







