Функциональные связи между параметрами конструкции, эксплуатационными показателями и условиями эксплуатации фасонных фрез

Данная статья посвящена исследованию функциональных связей между параметрами конструкции, эксплуатационными показателями и условиями эксплуатации фасонных фрез. А также построению матриц инцинденций используя установленные функциональные связи.

Ключевые слова: фасонная фреза, функциональные связи, матрица инцинденций

Наиболее распространенный способ обработки фасонных винтовых канавок предусматривает в качестве режущего инструмента фасонную дисковую фрезу или фасонный шлифовальный круг. Установка инструмента при обработке детали с винтовой поверхностью определяется относительным положением их осей и характеризуется в общем случае следующими параметрами:

– ψ — углом (или величиной l=pψ, где p — винтовой параметр), определяющим положение точки скрещивания осей инструмента и детали от исходного положения профиля;

– e — углом скрещивания осей;

– m — межосевым расстоянием.

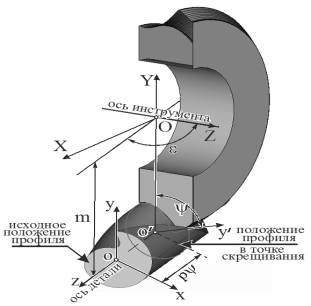
Рис. 1. Схема установки инструмента при обработке детали с винтовой канавкой

Большое количество проведенных исследований позволило определить, как внутренние функциональные связи между факторами процесса формообразования, так и внешние — между факторами и показателями.

Значение факторов, которые оказывают воздействие на процесс формообразования, определяется уровнем их влияния на показатели, которые определяют характеристики инструмента и обрабатываемой детали. Также они влияют на технико-экономические и ряд других показателей.

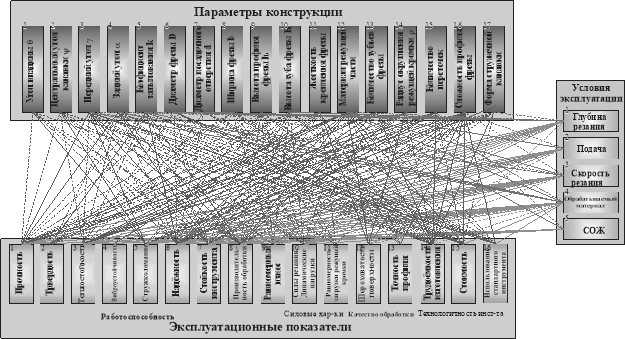
Рис. 2. Схема основных факторов и показателей процесса формообразования инструмента с винтовой канавкой

Для анализа и последующего использования при создании базы знаний процесса формообразования, а также для создания на ее основе САПР инструмента, основные функциональные связи между факторами процесса формообразования поверхности можно представить в виде матрицы МФ. Где Bij- элемент матрицы, которые в свою очередь включают в себя: совокупность функциональных зависимостей, различных табличных данных, сведений, связывающих между собой факторы процесса формообразования, расположенные в i–ой строке и j–ом столбце матрицы. Номер строки соответствует N — номеру фактора и изменяется в диапазоне от i =11,…,N для N<17, а номер столбца изменяется в диапазоне j=1,…,10, соответствует номеру фактора j=N-10 для N>10. Вид, структура и форма элементов матрицы МФ может быть различной, а при отсутствии установленных функциональных связей элемент матрицы Bij =0.

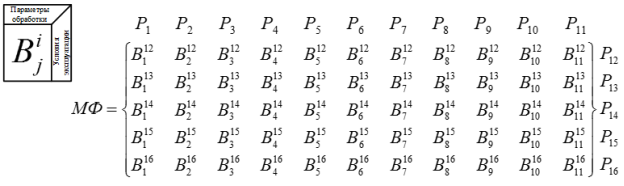
Рис. 3. Матрица МФ

Приведена трехмерная структура элемента матрицы B_i^j(B_i^j) обусловленная наличием большого количества достаточно сложных механизмов взаимодействия, как между факторами, так и между параметрами, от которых эти факторы зависят сами, но которые не входят в перечень анализируемых факторов i и j, т. к. являются предметом изучения и исследования в смежных дисциплинах, например, материаловедении, сопротивлении материалов и т. д.

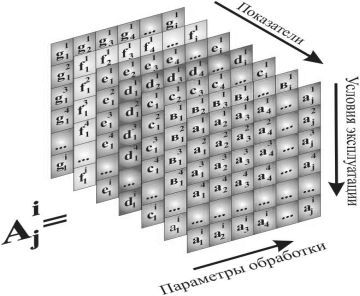
Рис. 4. Трехмерная структура элемента матрицы B_i^j(B_i^j)

Приведенные матрицы достаточно наглядно демонстрируют степень формализации процесса формообразования и возможные направления дальнейших исследований.

На основе матриц создается таблица, в которой указывается в каждом пункте 1 или 0, это обозначает установлена или не установлена взаимосвязь.

Матрицы инцинденций представлены в виде пульта графического интерфейса управления базой данных знаний процесса. Элементы матрицы представлены в виде клавиш трех цветов, содержание которых определяется степенью формализации функциональных связей. Использование данного представления матриц позволит в значительной степени формализовать процесс создания САПР инструмента. Кроме того, приведенная система позволяет оценить степень формализации и качество используемых функциональных связей. Благодаря этому можно сделать обоснованный выбор состава факторов и функциональных связей между факторами и показателями, исходя из конкретных условий формообразования.

Матрицы инцинденций могут также служить ориентиром в направлении развития исследований процесса формообразования. При этом сами матрицы связей МФ и МФП, по мере накопления знаний, будут претерпевать изменения как по составу факторов и показателей, так и по глубине формализации связей между ними.

Рис. 6. Матрица инцинденций представленная в графическом виде

На основании изложенного можно сделать следующие выводы:

– Процесс формообразования характеризуется большим количеством связей между факторами, которые целесообразно разделить на внутренние — параметры, и внешние — показатели.

– Совокупность функциональных связей, как между факторами, так между факторами и показателями, записанная в виде матриц функциональных связей, позволяет систематизировать и формализовать их представление.

– Матрицы функциональных связей представляют собой организационную структуру базы знаний процесса формообразования.

– Матрицы инцинденций, сформированные на базе матриц функциональных связей, представляют собой графический интерфейс системы управления базой знаний процесса формообразования.

– Матрицы инцинденций позволяют осуществлять планирование исследований по формализации функциональных связей процесса формообразования.

1. Петухов Ю. Е. Формообразование численными методами / Ю. Е. Петухов. — М.: «Янус-К», 2004. — 200 с.
2. Петухов Ю. Е., Домнин П. В. Формообразование фасонных винтовых поверхностей инструментов на основе применения стандартных концевых и торцевых фрез. — М.: ФГБОУ ВПО МГТУ «СТАНКИН», 2012. -130с.
3. Гречишников, В. А. Математическое моделирование в инструментальном производстве/ Гречишников В. А., Колесов Н. В., Петухов Ю. Е. — М.: МГТУ «СТАНКИН». УМО АМ, 2003. — 116 с.
4. Петухов Ю. Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства: дис, докт. техн. наук: 05.03.01 / Петухов Ю. Е.. — М., 2004. — 393с.
5. Петухов Ю. Е. Численные модели режущего инструмента для обработки сложных поверхностей / Петухов Ю. Е., Колесов Н. В. // Вестник машиностроения. — 2003. — № 5. — С. 61–63.
6. Петухов Ю. Е. Профилирование режущих инструментов среде Т-flexCAD-3D / Петухов Ю. Е. // Вестник машиностроения. — 2003. — № 8. — С. 67–70.
7. Петухов, Ю. Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Петухов Ю. Е., Домнин П. В. // Вестник МГТУ «СТАНКИН». — 2011. — № 3. — С. 102–106.
8. Колесов Н. В. Система контроля сложных кромок режущих инструментов / Колесов Н. В., Петухов Ю. Е. // ИТО: Инструмент. Технология. Оборудование. — 2003. — № 2. — С. 42–45.
9. Петухов Ю. Е. Компьютерная модель формообразования сложной поверхности / Петухов Ю. Е., Домнин П. В. // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т.: сб. науч. ст. — Тула, 2010. — Т. 1. — С. 197–200.
10. Колесов Н. В. Компьютерная модель дисковых фасонных затылованных фрез / Колесов Н. В., Петухов Ю. Е., Баринов А. В. // Вестник машиностроения. — 1999. — № 6. — С. 57–61.
11. Домнин П. В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений /Петухов Ю. Е., Домнин П. В. // Справочник. Инженерный журнал с приложением. — 2011. — № 11. — С. 26–29.
12. Колесов Н. В. Математическая модель червячной фрезы с протуберанцем / Колесов Н. В., Петухов Ю. Е. // СТИН. — 1995. — № 6. — С. 26–29.
13. Колесов Н. В. Два типа компьютерных моделей режущего инструмента Колесов/ Н.В., Петухов Ю. Е. // СТИН. — 2007. — № 8. — С. 23–26.
14. Петухов Ю. Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю. Е. Петухов, П. В. Домнин // СТИН. — 2011 — № 7. — С. 14–17.
15. Петухов Ю. Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю. Е. Петухов, А. А. Водовозов // Вестник МГТУ «СТАНКИН». — 2012. — № 3. — С. 28–32.
16. Петухов Ю. Е. Некоторые направления развития САПР режущего инструмента / Ю. Е. Петухов // СТИН. — 2003. — № 8. — С. 26–30.
17. Петухов Ю. Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю. Е. Петухов, А. А. Водовозов // Вестник МГТУ «СТАНКИН». — 2014. — № 1 (28). — С. 39–43.
18. Петухов Ю. Е. Определение задних кинематических углов при обработке винтовых фасонных поверхностей стандартными фрезами прямого профиля./ Петухов Ю. Е., Домнин П. В.// Вестник МГТУ Станкин. 2014. № 2 (29). С. 27–33
19. Петухов Ю. Е. Задачи по формообразованию при обработке резанием /Петухов Ю. Е., Колесов Н. В., Юрасов С. Ю.// Вестник машиностроения. 2014. № 3. С. 65–71.
20. Петухов Ю. Е. Компьютерное моделирование обработки винтовой канавки на заготовке концевой фрезы./ Петухов Ю.Е, Домнин П. В.// Известия Московского государственного технического университета МАМИ. 2011. № 2. С. 156–164.
21. Петухов Ю. Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS863310 04.05.1979
22. Петухов Ю. Е. Устройство для правки фасонных шлифовальных кругов. Патент на изобретение RUS 823101 21.03.1979
23. Петухов Ю. Е. Способ обработки цилиндрических поверхностей патент на изобретение RUS 904999 04.05.1979
24. Петухов Ю. Е. Прибор для профилирования червячных фрез. Патентнаизобретение RUS 878467 07.12.1978
25. Petukhov Yu.E. Some directions of cutting tool cad system development./Petukhov Yu.E.// Russian Engineering Research. 2003. Т. 23. № 8. С. 72–76.
26. Petukhov Yu.E. Curvilinear cutting edge of a helical bit with uniform life./Petukhov Yu.E.// Russian Engineering Research. 2014. Т. 34. № 10. С. 645–648.
27. Kolesov N. V. The mathematical model of a hob with protuberances./Kolesov N. V., PetukhovYu.E.// Russian Engineering Research. 1995. Т. 15. № 4. С. 71–75
28. Petukhov Y. E. Shaping precision in machining a screw surface / Y. E. Petukhov, P. V. Domnin // Russian Engineering Research. — 2011. — T. 31. — № 10. — С. 1013–1015.
29. Kolesov N. V. Computer models of cutting tools / N. V. Kolesov, Y. E. Petukhov // Russian Engineering Research. — 2007. — T. 27. — № 11. — С. 812–814.
30. Petukhov Y. E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y. E. Petukhov, A. V. Movsesyan // Russian Engineering Research. — 2007. — T. 27. — № 8. — С. 519–521.